用几何直观提高学生的学习能力
何晓玲
摘? 要 小学生的思维以具体形象思维为主,运用几何直观可帮助学生有效地将形象思维过渡到抽象逻辑思维,可以让学生调动各种感官,充分体验知识的形成过程,获得生动的表象,建立数学模型,并能熟练运用数学模型解决生活中的问题。
关键词 几何直观;课程标准;数学模型;学习能力;核心素养
中图分类号:G623.5? ? 文献标识码:B
文章编号:1671-489X(2020)01-0065-03
1 错题分析
五年级下册期末考试中有这样一道题目:
一个长方体,如果增高4 cm,就成为一个正方体,这时表面积比原来增加了96 cm2。原来的长方体的表面积是多少平方厘米?
这道题全班有14人做错,是整张试卷错误率最高的题目,错误率达到28.6%,错误类型有下面几种情况。
1)思路不清晰。一个学生的解答过程如下:
①96÷6=16(cm2);
②16×16×6=1536(cm2);
③(16×16+4×16+4×16)×2=768(cm2);
④1536-768=768(cm2)。
在这个学生的解答中,可发现他的第一步算式是没有算理的。他把96当作一个正方体的表面积,除以6得出16,看作一个面的面积;但后面又将16当成正方体的棱长,也就是长方体的长与宽;第三步又把“增高4 cm”这个数据当作长方体的高。因此,整个思路非常混乱。
2)表面积公式不熟,数据用错。
错题一:
①96÷4=24(cm2);
②24÷4=6(cm);
③6-4=2(cm);
④(6×6+6×6+6×2)×2=168(cm2)。
错题二:
①96÷4=24(cm2);
②24÷4=6(cm);
③6-4=2(cm);
④(6×2+6×2+2×2)×2=56(cm2)。
在第一个学生的解答中,第一、二步的解答思路没问题,求出的“6”既是正方体的棱长,又是原来长方体的长和宽;第三步求出的“2”是原来长方体的高;但在第四步运用表面积计算公式时,没有想清楚原来长方体的长、宽、高分别是多少,正确的解答应是(6×6+6×2+6×2)×2=120(cm2)。第二个学生的解答也存在类似的错误。
3)没有解答完整。有一个学生的解答如下:
①96÷4=24(cm2);
②24÷4=6(cm);
③6-4=2(cm)。
从这个学生的解答中可以看出,他知道一些解答步骤,但求出这些结果后,不知这些结果能做什么,属于思路不清晰、解答不完整。
对以上分析进行反思:到底要教给学生怎样的学习能力?怎样提升学生的核心素养?笔者认为运用几何直观能很好地帮助教师解决这个困惑。
《义务教育数学课程标准(2011年版)》指出:“几何直观主要是指利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明、形象,有助于探索解决问题的思路,预测结果。几何直观是学生空间观念形成的基础。小学生的思维以具体形象思维为主,几何直观能力是思考数学问题、发展数形结合思想的基础,是学生必备的一种基本数学素养。教师在教学中应充分运用几何直观使知识形成生动表象,形成概念,促进学生有效思维,提高学习能力,培养学生的数学学科核心素养。
2 借助实物操作,直观感受表面积变化规律
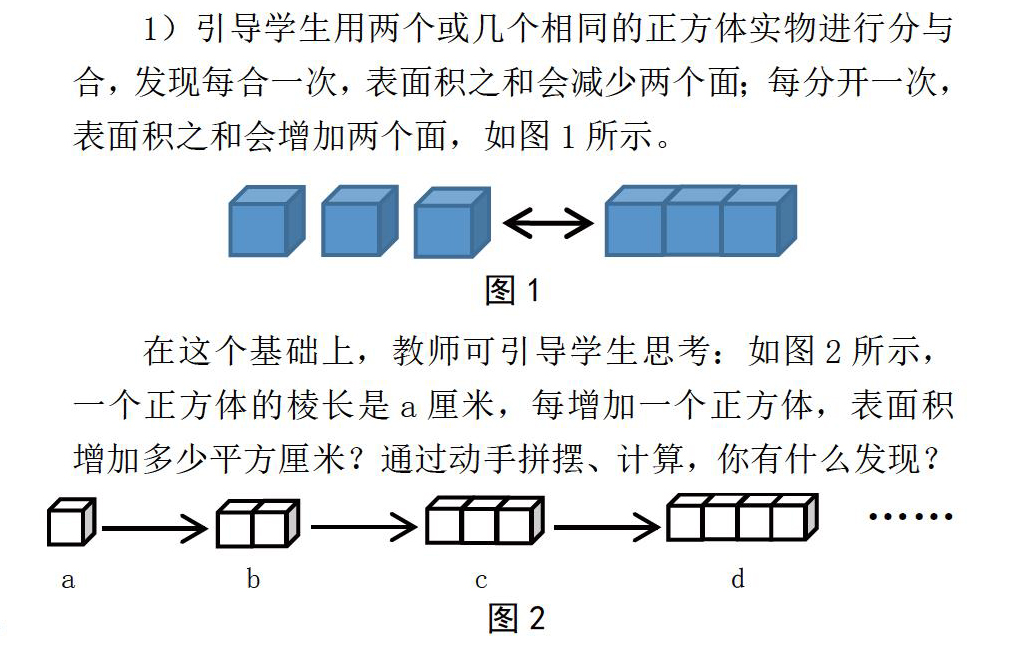
1)引导学生用两个或几个相同的正方体实物进行分与合,发现每合一次,表面积之和会减少两个面;每分开一次,表面积之和会增加两个面,如图1所示。
在这个基础上,教师可引导学生思考:如图2所示,一个正方体的棱长是a厘米,每增加一个正方体,表面积增加多少平方厘米?通过动手拼摆、计算,你有什么发现?
学生独立思考,动手操作,小组合作探究,交流讨论,展示不同的思路。
【生1】從图2a到图2b,表面积之和减少两个面,所以可以用6a2×2-2a2=10a2
【生2】可以先找出每幅图长方体的长、宽分别是多少。从这四幅图中可以看出,图2b的长是2a厘米,图2c的长是3a厘米,图2d的长是4a厘米;宽和高不变,都是a厘米。运用长方体的表面积公式计算,图2b的表面积是(2a×a+2a×a+a2)×2=10a2,同样计算方法可以算出图2c、图2d的表面积分别是14a2平方厘米,18a2平方厘米,每个图形都比前一个图形多了4a2平方厘米。
【生3】从图中可以看出,每个图形露出的正方形的个数是有规律的,不变的是左右两个面,变的是每次多了前、后、上、下四个小正方形,只要算出每个长方体是由几个这样的小正方形围成的,再乘每个正方形的面积,就可以算出表面积了。图2c有3×4+2=14个小正方形,长方体的表面积就是14a2平方厘米;如果是图2f,就有6×4+2=26个小正方形,长方体的表面积就是26a2平方厘米。
教师再抛出问题:如果是n个小正方体拼成的长方体,它的表面积是多少平方厘米呢?有了前面的基础,学生就能很快地推理出n个长方体表面积为(4n+2)a2平方厘米。
长方体或正方体的拼摆过程真正让学生动手去操作,通过摸、摆、拼、剪等具体行动,让学生感知表面积中的变与不变,通过操作、观察、分析等活动发现规律。这样才能实现学生主体真正的发展,教学才能真正有效落实。
2)将两个相同的长方体不同方向拼摆,找分与合表面积的变化。
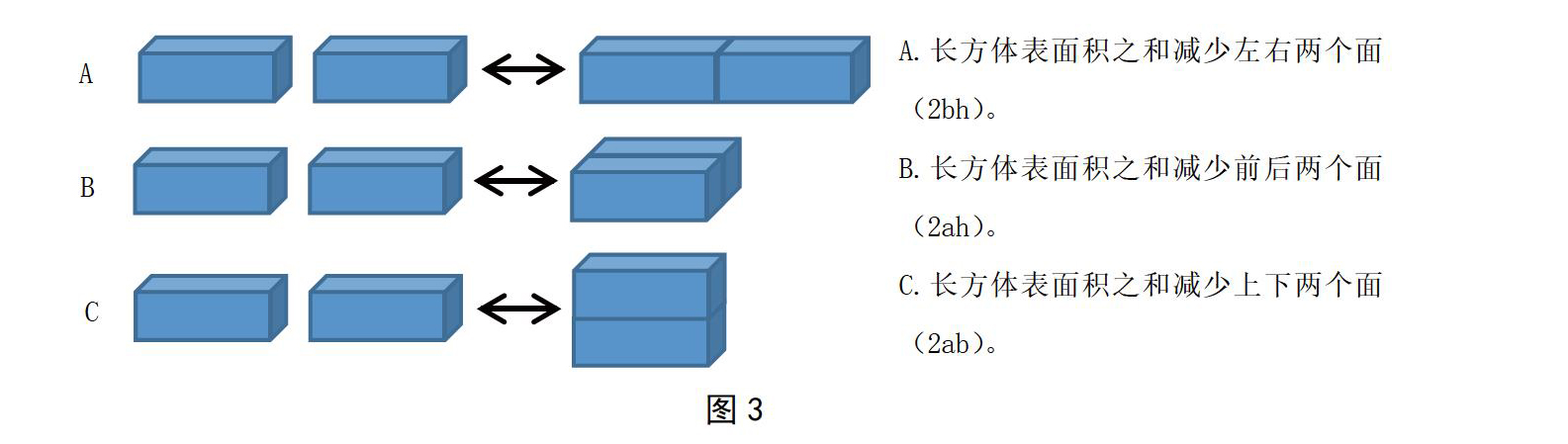
拼一拼、说一说:如图3所示,将两个完全相同的长方体合在一起,表面积之和会发生什么变化?你发现了什么?
学生动手操作,独立思考,小组合作探究,交流讨论,发现有三种不同的拼摆方法,表面积减少是不同的:将最大的面合在一起,表面积减少的最多;将最小的面合在一起,表面积减少的最少。反过来,如果将一个长方体截成两个长方体,表面积增加最多的就是平行于最大的面切开,表面积增加最少的就是平行于最小的面切开。
3 用几何直观促知识的理解与内化
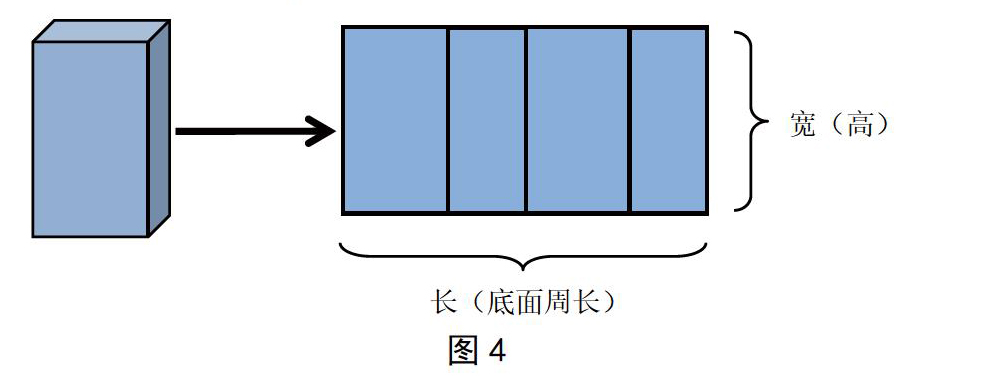
在教学五年级下册“长方体和正方体”这个单元的知识时,学生第一次接触立体图形,对空间的想象有很大的难度。因此,多让学生动手摸一摸、摆一摆、涂一涂、折一折,丰富学生的表象,多角度地观察与思考,找到解决问题的方法。在这个单元中,学生最不易掌握的就是长方体的表面积计算,因为根据生活实际情况,有求表面积有六个面,也有求五个面(无盖、粉刷教室等),还有可能求四个面(烟囱、饼干盒贴商标等)。在求长方体四个面(前后左右)的面积时,很多学生会用“长×高×2+宽×高×2”,或者用“(长×高+宽×高)×2”这两种方法。教师这时可让学生拿一个没有上、下底的纸盒沿高展开,发现展开图是一个大的长方形,这个长方形的面积就是前后、左右四个面的面积之和,如图4所示。
这个长方形的长就是长方体底面周长,宽就是长方体的高,所以这四个面的面积之和还可以通过“底面周长×高”计算出来,也说是用“(长+宽)×2×高”来计算四周的面积,在此基础上加上面的面积和下面的面积,就可以求出表面积。这样就将求长方体的表面积转化成求一个平面图形的面积。通过让学生动手剪一剪、摆一摆、比一比,学生掌握了多种求表面积的方法,并能结合直观图有理有据地说出自己的想法。
4 学会用画图方法帮助理清解题思路
除了动手操作充分感知,教师应引导学生学会用图来分析题意、理解题意、理清解题思路,能主动用图说事、用图分析、用图说理。学生的作图能力不是与生俱来的,他们需要教师正确的引导与示范,并进行学习与练习。教师可在学生大量观察各种各样的长方体、正方体实物或模型的基础上,提出问题:在观察长方体、正方体时,最多能看到几个面?
如图5所示,教师示范画出能看出三个面的长方体、正方体,先画正面(长方形或正方形),再画另两个面(平行四边形),并在合适的位置标上数据。让学生学着画,教师要鼓励学生,对画得好的学生及时表扬,展示其作品;对画得不够好的学生,应指出不足在哪里,并引导他重新画,直到画好为止。
学生在根据题意会画图的基础上,还要看懂图意,会分析、理解图意。如这道题:
一个长方体,如果增高4 cm,就成为一个正方体,这时表面积比原来增加了96 cm2。原来的长方体的表面积是多少平方厘米?
根据题目的描述“一个长方体,如果增高4 cm,就成为一个正方体”,作图时就可先画出一个正方体,然后标出增高的4 cm,这样就把正方体分割成两个长方体,如图6所示。从图6中可以看出,每个长方体都有两个相对的面是正方形,长和宽是相等的,前、后、左、右四个面的面积是相等的。
增高4 cm,表面积增加96 cm2,增加的面积在哪儿呢?这是本道题解题的关键。因此,画出图后会正确地看图,是每位学生必须掌握的本领。教师在引导学生观察图形之后,思考问题:增高之后,表面积增加在哪儿呢?学生经过思考、讨论、交流发现,表面积并没有增加六个面,因为两个长方体拼在一起后,中间两个面合在一起隐藏了,不能算表面积的一部分,这样下面这个长方体只剩前、后、左、右、下等五个面。如果要使下面一个长方体的表面积不变,就要将上面一个长方体的上面割补移到下面长方体的上面(抵消法),真正多出来的表面积只有上面长方体的前、后、左、右等四个面,如图7所示。
如图8所示,这道的解题思路是:
①先求每个面的面积(或展开图的底面周长):96÷4=
24(cm2);
②再求长方体的长或宽:24÷4=6(cm);
③再求原来长方体的高:6-4=2(cm);
④最后求原来长方体的表面積:
s=(ab+ah+bh)×2
=(6×6+6×2+6×2)×2
=120(cm2)
用几何直观画图理解有关“增高”引起表面积增加的问题,也可以解决“降高”引起表面积减少的问题。通过对比发现,不管是“增高”还是“降高”,表面积始终变的只有四个面的面积,都可以先找展开图的底面周长或者每个面的面积,这就是这道题的解题关键。这样就建立起数学模型,以后遇到类似的题目,都可以用这个数学模型去解决。
教师通过安排合理的操作环节,给学生提供更多亲自动手实践的机会,同时给学生提供了更大的思维空间。在动手操作过程中,学生就会把操作与思维联系起来。动手操作可以使学生对知识产生新的理解和看法,进一步理解和巩固知识,还能够在新的发现、新的感悟中碰撞出创新意识的火花。
5 结语
总之,几何直观能利用图形描述和分析问题,借助几何直观,让学生用摸、摆、拼、剪等动手操作形成生动、丰富的表象,把复杂的数学问题变得简明、形象。几何直观可以帮助学生理解抽象的数学知识,感知知识的形成过程;可以帮助学生建立数学模型,进而运用数学模型解决生活中的问题。“授之以鱼,不如授之以渔。”教师不但要善于使用几何直观进行教学,还应指导学生主动运用几何直观学习,用画图的方法分析题意、理解题意、理清解题思路,从而提高学生的学习能力,培养学生的核心素养。
参考文献
[1]孔凡哲,史宁中.关于几何直观的含义与表现形式:对《义务教育数学课程标准(2011年版)》的一点认识[J].课程·教材·教法,2012(7):92-97.

