高中教材中数学建模问题设置的研究

    洪雨沛

    

    

    摘要：数学建模核心素养的培养离不开对建模问题的研究与探讨。本文梳理了现行高中数学理科教材中的数学建模问题，从问题情境、知识内容、建模流程的完整性、问题呈现形式与设置意图等方面进行了研究，并为教材建模问题的设置提出了一些建议。

    关键词：数学建模;核心素养;教材分析

    数学建模作为高中数学六大核心素养之一，引起了社会广泛的关注。高中数学教材中数学建模问题的设置直接影响学生数学建模核心素养培养的效果。本文选取人民教育出版社（A版）与上海教育出版社（以下简称人教A版和沪教版）出版的高中数学（理科）教材，对其中数学建模问题的设置进行研究。

    一、研究工具

    1.数学建模与数学应用题的差异

    数学建模的特点：问题来源于现实生活，原汁原味;因为现实生活的复杂性，为了简化模型，往往需要提出一些合理的假设;模型多样化，可以不断地优化完善;得到的结果需要返回现实情境中进行检验。应用题是编者根据现实情境进行合理简化后编制而成的，有浓厚的“人为编制”的味道。另外，应用题的解答流程与建模问题的解答流程并不完全一致，往往应用题都有明确的答案，模型也较为单一。

    2.问题选择原则与分析框架

    根据数学建模的内涵，我们将教材中符合以下条件的问题整理出来：

    （1）问题的情境为现实情境或科学情境;

    （2）具备最基本的数学建模过程（将现实问题转化为数学问题、建立模型、求解模型、返回现实中解决问题）

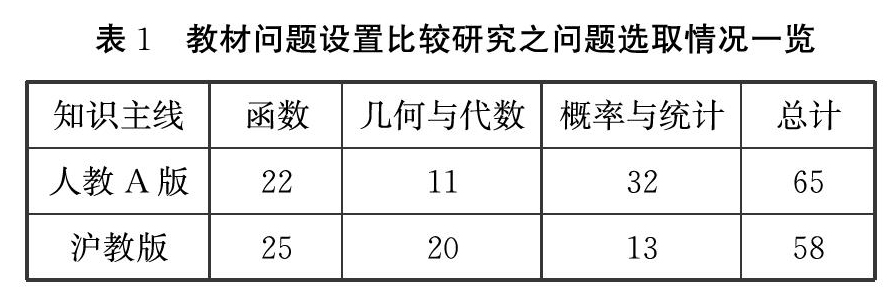
    对于多个类似的问题，我们将选取1～2个问题作为代表问题进行分析。按照这样的原则，共选取123个问题，具体情况如表1：

    两个版本的问题数量相差不大，其中概率与统计主题人教A版选例较多，原因是人教A版教材中概率与统计内容比沪教版多。人教A版几何与代数选例较少，原因是在解析几何部分大多以数学情境为背景让学生直接进行计算求解，而沪教版有较多的现实情境实例让学生加以练习。

    值得注意的是，数学建模问题与我们常说的应用题是有差异的，但考虑到高中数学教材的特殊性，只要满足以上两个条件，无论是否有应用题的属性特征，都被视作本研究中所提到的数学建模问题。

    对于选择出来的问题，将从以下角度进行分析研究：

    （1）该问题的呈现形式是什么？设置的目的是什么？

    （2）该问题的问题情境是哪一类？（《普通高中数学课程标准（2017年版）》将问题情境分为现实情境、科学情境与数学情境。）

    （3）该问题主要涉及哪些知识内容？

    （4）解决该问题所建立的模型是否唯一？能否让学生经历“模型的改进”这一步骤？

    二、教材研究

    1.问题的呈现形式

    两版教材中的数学建模问题，都是应用题占主导地位，但也有一些探究性学习或活动，这一点在沪教版教材中尤为明显。沪教版教材会设置一些课题，让同学们围绕课题进行思考、讨论与研究，课题有时会涉及一些试验的设计与数学建模论文的撰写。而人教A版教材中的探究性学习内容较少，但会出现较多的方案设计题，要求学生根据具体的情境设计出符合要求的方案。研究性课题和方案设计问题对学生的要求，都要高于应用题，这些问题更加贴近生活，使学生综合运用知识的能力得到较充分的锻炼。

    通过对两版教材建模问题的分析发现，问题设置的目的大致可以分为三种。一是借用数学建模问题，介绍新的知识或新的数学模型。这样能够让学生在现实情境中自然地学习新的数学知识，更加深刻地感受新知识的应用价值。二是对学生运用数学知识解决问题的能力进行检测，通过一系列问题的设置，探查学生对知识的掌握程度。三是要求学生真正地解决生活中的一些问题，这类题目相对较少，主要出现在沪教版教材中，并且大多以课题的形式出现。

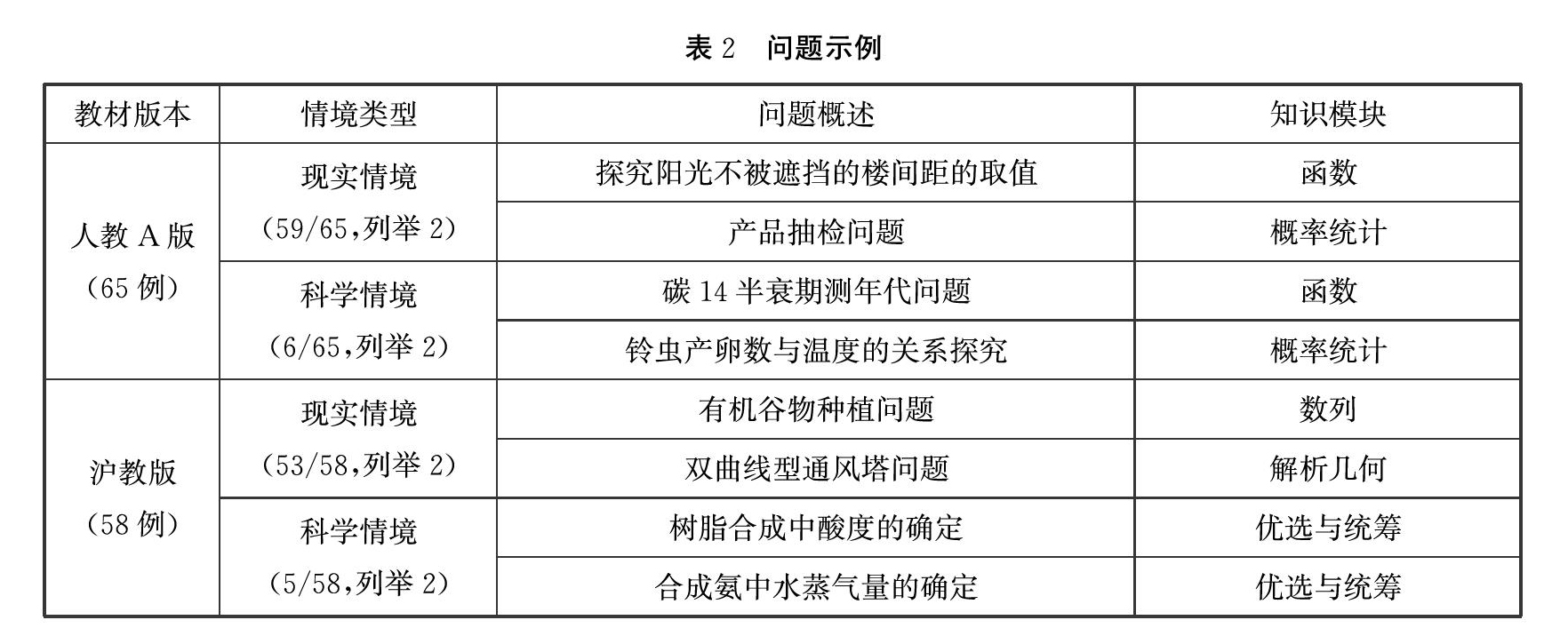
    2.問题情境与知识内容（如表2）

    两版教材中的建模问题大都以现实情境为背景，科学情境占少数。总体来看，问题背景较成熟，多为社会中的实际问题，并且问题涉及范围较广，与学生距离较远，如人口增长率、地震级数、半衰期等。部分问题也具有积极的导向，如保护环境、合理调整自己的情绪等。部分问题也能帮助学生形成正确的社会价值观，如厂家生产合格产品等。相比于沪教版教材，人教A版教材问题所涉及的范围更加广泛。

    教材中的建模问题，有些要求学生能够熟练地运用初等函数模型去探究变量与变量之间的（确定）关系，并对一些现象进行解释和预测;有些问题要求学生能够从现实情境中抽象出三角形模型，并使用正余弦定理等工具进行求解;有些问题要求学生运用线性规划的知识去寻找最优策略，并对现实问题进行最佳决策;有些问题需要学生运用解析几何的知识加以解决。

    概率与统计模块的知识内容在建模问题中也有大量的涉及。有些要求学生能够根据具体的情境设计抽样方案;有些要求学生能够借助于一组数据的特征值对数据进行分析并对现实问题做出合理的判断;有些要求学生利用计数原理与排列组合进行计数或计算古典概型的概率;有些要求学生能够通过建立回归方程去了解两个变量之间的相关关系（沪教版教材不涉及相关内容，故无无此类问题）;有些要求学生能够对两个变量进行独立性检验，判断是否显著性相关。

    从知识内容上看，两版教材中的建模问题差异不大，重点考查的知识内容基本一致。但在解析几何模块，沪教版教材的建模问题较多，而人教A版大多以数学情境为背景让学生直接进行计算求解。

    3.建模问题的解决过程

    根据《普通高中数学课程标准（2017年版）》对数学建模内涵的确定，我们可以认为一个数学建模问题的解决，要经历将现实问题转化为数学问题—建立模型—求解模型—模型的改进—将结果返回现实中解决问题等一系列流程。在教材梳理的过程中，我们没有将“模型的改进”作为一项问题筛选的指标，因为大多数建模问题的模型以及结果都是唯一确定的，并没有给学生改进模型的空间。在选取的123例中，只有24例在数学建模的过程中涉及模型的改进，其中人教A版独占20例。而所涉及的问题主要是变量关系的确定或方案的设计，因为这类问题往往没有标准答案，故学生可对自己选择的模型进行改进与优化。如变量关系的确定，有些关系可以用多种函数模型加以描述，当学生选择一种模型完成数学建模解模后，他们可以选择另外一种模型进行描述，并对两种模型进行比较，若后者优于前者，则可以对之前的模型进行完善。方案的设计也是如此。

    三、建议

    学生在数学学习中接触较多的是传统的应用问题，对数学建模问题相对陌生，其主要原因是数学教材中，纯正的数学建模问题较少，教师没有抓手，无法进行相应的教学。根据对教材的研究，笔者认为教材中的建模问题应尽可能具备以下特征：①问题情境应尽量保留最原始的现实情境，不要做过多的简化与假设，否则在学习的过程中，学生缺乏对问题的分析和假设，自身的思维品质和创新能力将无法得到提高;②解决问题的模型应具有多样性，并且不同的模型能够反映学生的不同水平。正如张思明总结国外教材变化时所说，应用题要向数学建模问题不断过渡，表现为：问题的来源更生活化，更贴近实际;条件和结论更模糊;可用信息和最终结论更有待学生自己的挖掘。另外，以建模问题为工具进行新知识、新模型的教学是一个不错的手段;较复杂、较综合的建模问题可以以课题、探究性活动等形式呈现。

    除了教材中数学建模问题的设置需要进行适当调整外，教师对数学建模的态度以及教学方式也需要有所改变，不能按照以往的应用题的教学方式去教授数学建模。另外，在学生掌握常见数学模型的同时，也要鼓励学生打开思路，对数学模型进行不断的挖掘与创新。

    责任编辑：黄大灿