浅析几何画板如何延伸数学思维触角

    王维

    

    

    

    摘要：信息技术的飞速发展带动教育技术的革新。数学课堂应该合理运用信息技术，化静为动，化抽象为直观，发展学生的空间想象能力，由传统训练型课堂转变成探究型课堂。本文主要阐述在常规课堂上运用信息技术，帮助学生深度思考，提升思维能力。

    关键词：信息技术;拓展想象;数学素养

    学生的认知是直观的，而数学最重要的特征是抽象性，数学课堂如何在这两者之间达到平衡，成了老师不断探索的主题。如果偏重直观教学，那会影响学生的想象广度;如果偏重训练技能，那又势必限制学生的思维发展。借助于信息技术，能帮助学生延伸思维的触角，拓宽空间想象能力，突破教学上的难点。

    一、观看直观操作过程，感受空间表象，进行“可视性学习”

    具体直观的展示深受学生们的喜爱，利用新技术展示直观操作，是对教学的有力补充，能够拓宽学生的想象空间。学生通过认真观察，做好记录，加上思考、操作、讨论等过程，能发现数学动中有静、变中不变的规律。

    在《长方体和正方体》的教学中，会遇到这样的问题：一张长方形纸片，长6厘米，宽4厘米，分别绕着长和宽各旋转一周，求它的体积和面积。学生只有清楚得到的图形，才能计算出它的体积和面积。再如：一张三角形硬纸板，分别绕着两条直角边，旋转一周，能够形成什么，并计算它们的体积。

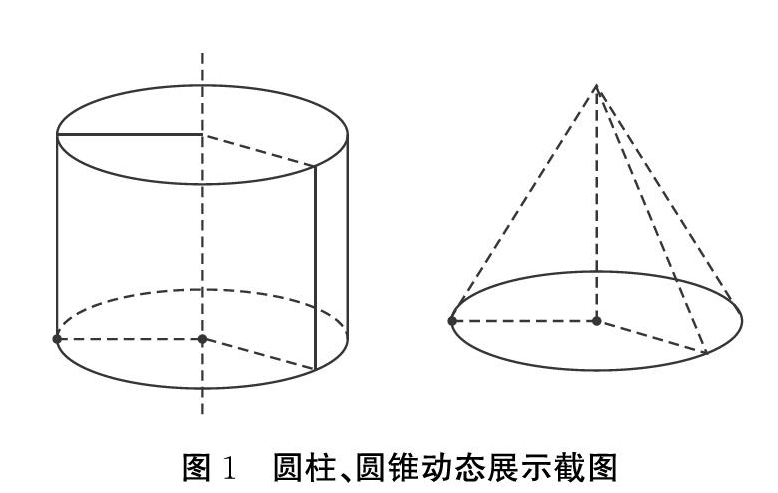
    这类问题，很多同学想象不出具体的图形，对旋转过程不是很清楚，我们可以利用几何画板演示旋转的过程（图1）。这样，化抽象化为直观，变静态学习为动态学习，为学生思维搭建“脚手架”，体现了儿童可视性原则。

    二、丰富表象，初步培养空间想象能力，进行“探究性学习”

    教材中很多实践活动的内容，能发展学生的兴趣，提升思维能力和积累活动经验。这些实践活动都是以学生为主，通过其不断尝试，培养分类讨论能力、假设验证能力、数形结合能力等。

    在苏教版四年级下册《认识三角形》中，有一个探究活动是给出三个点，探究能够连出几条线段。探究活动的目标是，不在同一条直线上的三点才能围成三角形，而在同一条直线上的三点不能围成三角形。教师可利用几何画板，分类演示，弥补学生思维的盲点，使学生深刻感受到：三条线段在同一条直线上，围不成三角形。

    通过此探究性学习，能发展学生的研究能力，为今后的分类探讨研究打下了基础。

    三、设计图案，动手操作，进行“设计性学习”

    教材中有很多动手做一做、画一画等图形设计之类的练习。在传统教学中，它们都是容易被忽视的。纸张和绘画工具的限制，都让本来趣味十足的学习蒙上了灰尘，比如苏教版六年级下册《图形的运动》这一节，教材安排了动手设计这一环节，学生可以利用几何画板，轻松设计出美丽的图案。

    四、运用几何画板，加强空间想象，进行“创造性学习”

    推理能力的高低反应数学思维深度发展程度的高低，发展推理能力是数学课堂努力的方向。而在这个发展的过程中，要充分发挥学生的主体作用，在对几何图形的认知中，加深对模型的建立，形成推理能力。

    下面以几何画板在突破《圆的面积》教学上的难点为例。

    几何画板应用分析：

    1.动态演示圆的面积的概念，一条线段绕着一个端点，旋转一周，求圆所占平面的大小，趣味导入。

    2.利用几何画板的度量功能，方便快捷地获取数据，迅速得到圆的面积和正方形面积的数据，重点进行数据之间联系的探索，节省时间。

    3.直观感受“化圆为方”的过程，突破思维障碍，真实感受极限思想。

    课堂部分环节展示：

    师：圆的面积，该如何转化呢……

    生：通过“剪、移、拼”三步骤的方法，化未学为已学。

    师：圆怎样剪？想剪成什么样？（尝试操作）能沿着边缘剪吗？

    生：不能沿着边剪，因为圆的边是曲线，可以沿着半径平均分。

    生：把这个圆，沿着直径剪开，平均分成四部分，拼起来像平行四边形。

    师：（追问）还能像得多一点吗？

    生：可以。我們继续平均分，份数多一些。

    师：好的，现在平均分成了8份。

    生：现在越来越像平行四边形了。

    师：（追问）还可不可以更加像平行四边形呢？

    生：可以！

    师：现在把圆平均分成16等份。

    生：现在更加像平行四边形了。

    师：猜想一下，我们分的份数继续增多，会发生什么？

    生：圆会变成平行四边形。

    师：真的是这样吗？请几何画板来帮忙。

    仔细观察……

    师：这是圆被平均分成40份的结果

    师：这是圆被平均分成160份的结果

    师：你现在怎么认为的？（问刚才猜想的同学）

    生：有点像长方形了…

    师：噢，有点像长方形了吧。再看这是圆被分成320份的结果。

    师：那我们来研究一下这个长方形和之前的圆有什么关系……

    【设计意图】 学生一开始受思维的局限，猜想圆会变成平行四边形，紧接着沉醉在这种猜想里面，似乎理所当然。可随着几何画板的演示，看到圆被分的份数越来越多的情况时，学生自然打破原有观点，重新建立新的猜想，不断激发探索求知欲，思维得到一次又一次的提升。几何画板方便快捷的直观展示，有利于提升学生的演绎推理能力。

    适当地运用信息技术，可建立展开图与立体图形之间的关系，使学生对几何图形有更深刻的认识。小学阶段空间观念的形成与发展，与其今后几何进一步的学习有着密切的关系。巧妙地利用信息技术，准确地把握学生空间观念的发展方向，有的放矢地引导学生发挥想象，利用模型，促进其推理能力的发展，激发学生的观察兴趣，在潜移默化中提升学生的探究能力，形成新时代应具备的数学思维品质，能为学生终身学习打下良好的基础。

    参考文献：

    [1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

    [2]罗永军.探索之乐——“新思维”数学实验课程的开发与实施[J].小学数学教师，2015（7，8）：5559.

    责任编辑：黄大灿?赵潇晗