培养高中数学核心素养的教学实践研究

    胡媛媛

    

    

    

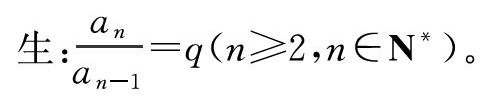
    摘要：以“等比数列”为例，探究在数学教学中如何将数学核心素养的培养融入课堂的各个环节，合理设计教学过程，让学生体会等差与等比的异同，并取得较为理想的教学效果。

    关键词：核心素养 ?等比数列 ?情境

    一、研究背景

    教育部明确要求各个学校要结合学生的特点与实际情况，把核心素养的培养落实到教学过程中。《普通高中数学课程标准》中明确定义了数学学科核心素养的概念，指出了其组成要素及其之间的联系。目前，此方面研究方兴未艾，章建跃从教材编写一般规律的角度，探讨核心素养的落实;孙成成讨论了数学核心素养的发展路径。这些丰硕的研究成果，极大地推动了学科发展。而把数学核心素养融合于教学活动中，有利于学生的全面发展。

    二、剖析内容，梳理难点

    等比数列是教材中的第二个特殊数列，如何在核心素养的视角下设计教学过程？笔者遇到了下面的几个困惑：

    （1）如何合理设计情境，引导学生发现规律，自然地引出概念，培养学生数学建模与抽象的能力？

    （2）能否用一个数学情境贯穿始终，使课堂形成一个整体？

    （3）如何设计教学活动，连接教学内容，使教学过程衔接自然，培养学生逻辑推理与直观想象的能力？

    （4）如何设计例题与练习，加深内容理解并巩固掌握，培养学生数学运算与分析的能力？

    三、科学设计，提升素养

    1.创设情境，引入新课

    探究：如果能将一张厚度为0.1毫米的《大江晚报》第一次对折，第二次对折，第三次对折，……（假设可以一直折下去），那么，对折30次后，你觉得这时报纸的厚度更接近于（ ??）。

    A.《新华字典》的厚度（3厘米）

    B.迪拜塔的塔高（828米）

    C.合肥市区到芜湖市区的直线距离（约122千米）

    D.地球与月球之间的平均距离（约38万千米）

    【设计意图】通过对报纸对折后厚度的猜测，引起学生探究问题的兴趣，发生思维碰撞，激发学生问题再探的兴趣。

    通过对对折后报纸的层数变化及面积变化的研究，抽象出如下四个数列：

    师：请同学们仔细观察上面的四个数列并认真思考，上面叙述的数列有哪些共同的特征？

    生：相邻两项的比是一样的。

    师：我们在等差数列里面是不是也得到过类似的关系？那么，相邻两项的比是一样的数列，我们是不是也可以给它一个新的称呼？

    生：等比数列。

    【设计意图】从一个实际问题中抽象出了四个等比数列，这里既有时间上的考虑，也有对不同公比等比数列的展示，培养了学生核心素养中数学建模的能力。

    2.探究新课，理解概念

    师：你能参考我们之前学习过的等差数列，尝试写出等比数列的定义吗？

    （1）定义：一般的，如果一个数列从第2项起，……

    师：你能尝试用符号语言来定义等比数列吗？

    【设计意图】类比是本节课中运用的主要思想，所以在等比数列定义的归纳与整理部分采用了这一思想。类比思想的渗透，提升了学生数学抽象的核心素养。

    （2）等比中项

    师：两项能构成等比数列吗？

    生：不能。

    师：那最简单的等比数列至少需要几项？

    生：三项。

    师：如果一个等比数列的第一项是1，第三项是9，你能求出第二项G吗？

    生：3，或者-3。

    师：你是如何得到第二项的呢？

    师：一般的，如果a、G、b是等比数列，那么G叫作a与b的等比中项。

    师：你能写出G与a、b的关系吗？

    师：那么，这时对a、b有什么要求？

    生：同号。

    【设计意图】从最简单的等比数列出发，有意识地引导学生形成从简单到复杂，从特殊到一般的思维方式。引导的过程，着力使学生感受知识的形成过程是自然的，在求解过程中追本溯源，引导学生找到问题的根本。

    让学生自己列举出一些等比数列的例子，并抽出部分进行点评。

    师：同学们列举的数列很丰富，数列中的项有正数，也有负数，但是没有零，那么，零可以作为等比数列的项吗？

    生：不能。因为不满足定义，所以等比数列的任何项都不能为零。

    师：这里我们还看到了非零常数列，它是等比数列吗？公比是多少？

    生：是的，q=1。而且，非零常数列是一类特殊的既等差又等比的数列。

    【设计意图】学生自己举例，感受等比数列的特性，再通过问题引导帮助学生更好地理解等比数列的定义，同时用投影显示学生举例，规范数列的写法。

    师：你是怎样得到这个数列的？

    生：先确定首项，再确定公比。

    师：此数列的第85项是多少？有没有更便捷的方式能直接得到数列中的项呢？

    生：利用通项公式。

    师：如果我们已知等比数列中{an}，首项为a1，公比为q，你能类比等差数列，获得等比数列的通项公式吗？（学生自主推导）

    【设计意图】从学生举的例子出发，通过问题引导学生一步步地归纳出确定等比数列的首项与公比，让学生自己去类比、归纳和推导，发现并理解，提升逻辑推理的核心素养。

    （4）图像

    引导学生從解析式和图像两个角度研究等比数列和与其对应的指数型函数的关系。从图像上看，表示数列中各项的点都在与其对应的指数型函数图像上，它们是函数图像上的一些孤立的点。因为数列是以正整数集或其有限子集为定义域的特殊函数。

    【设计意图】让学生从数（结构特征）与形（图像）上进一步认识到等比数列的通项公式与指数型函数之间的关系，培养学生直观想象的能力。

    3.讲解例题，加深理解

    例1：一个等比数列的第2项和第3项分别是8和12，求它的第1项和第4项。

    例2：一个等比数列的第1项和第3项分别是2和4，求它的第2项。

    变式练习：一个等比数列的第1项和第5项分别是2和4，则它的第3项是 ???。

    思考：（1）在等比数列{an}中，每隔k项取出一项组成一个新的数列，这个新数列是等比数列吗？

    【设计意图】让学生熟悉概念与公式，加深对本节内容的理解，并培养学生数学运算、数据分析的核心素养，同时引出下一节课的探究内容，为第二课时埋下伏笔。

    4.课堂小结，类比归纳

    师：你能类比已学过的等差数列的知识，回顾今天所学习的内容吗？

    【设计意图】列出表格，对比联系，清楚直观。

    5.情境回顾，前后呼应

    师：我们现实生活中，有很多等比数列的模型，你能想到哪些？（设置讨论）

    师：从数学的角度抽象了现实生活中与等比数列相关的模型，那我们今天最开始的时候，是不是也有一个等比数列的模型？现在，你的选择有改变吗？

    生：由于对折后报纸的层数是a31=230，所以对折后报纸的厚度是0.1×230毫米，约等于107千米，所以应该选C。

    师：很好。所以，我们现实生活中很多问题需要进行精准的数学分析。

    【设计意图】从实际问题中来，再回到实际问题中去，用一个数学情境贯穿始终，使课堂成为一个整体，激发学生数学学习的兴趣，并回归认识现实生活中的数学现象。

    四、教学思考

    本节教学融合了类比、归纳、数形结合教学思想，实现了“现实情境—数学模型—回归实际问题”的递进过程，注意了数学知识的内在联系，并侧重培养了学生的数学核心素养，但在通项公式与方程思想的渗透上稍有欠缺。就课堂反馈情况来看，教学引导比较合理，讲解较为透彻，实现了重点突出、前后呼应的效果，师生互动良好而有效，课堂气氛融洽，收到了预期的教学效果。

    参考文献：

    [1]中华人民共和国教育部.教育部关于全面深化课程改革落实立德树人根本任务的意见[EB/OL].[2014-04-08].http：//www.moe.gov.cn/srcsite/A26/jcj_kcjcgh/201404/t20140408_167226.html.

    [2]中華人民共和国教育部.普通高中数学课程标准（2017年版）[M].北京：人民教育出版社，2017.

    [3]章建跃.高中数学教材落实核心素养的几点思考[J].课程·教材·教法，2016，36（7）：44-49.

    [4]孙成成，胡典顺.数学核心素养：历程、模型及发展路径[J].教育探索，2016（12）：27-30.

    [5]中学数学课程教材研究开发中心.普通高中课程标准实验教科书·数学·必修5[M].北京：人民教育出版社，2007.

    责任编辑：黄大灿