调度问题中的算法

    陈道蓄

    

    

    

    说到“调度”，人们往往会想到交通运输部门的运行安排，也会想到企业中复杂的生产任务安排。其实，日常生活中也经常面临着多个事项需要合理安排;只不过任务数不大，也不涉及明显的经济指标限制，人们凭经验就足以应付，很少会联想到“算法”。当需要解决的任务数增加，且包含相互依赖关系时，算法可以帮助我们顺利有效地完成任务。

    ● 单纯依赖关系约束下的任务调度

    我们从仅考虑任务间的依赖约束开始。如果任务X只能在另外某个任务Y完成后才能开始，我们就说X依赖Y。下面来看一个简单的例子。

    同学们打算在教室里组织一场联欢活动，还准备自己动手包饺子。他们拟定了一张准备工作任务表，包含所有任务事项、每项任务耗时、任务间依赖关系（注意：只需列出直接依赖关系，而间接依赖关系自然地隐含在其中）。管理上通常将这些任务的集合称为一个“项目”。任务列表见表1。

    有些任务之间没有依赖关系，执行顺序无关紧要，如果有多个执行者，这样的任务就可以并行。这里说的“调度”，就是要给每项任务分配一个不同的序号，表示它们执行的顺序，满足：如果任务X依赖任务Y，则X的序号就要大于Y的序号;如果两个任务之间没有依赖关系，则对它们的序号关系没有要求。从数学上看，原来所有任务间的依赖关系确定了一个“偏序”，即并非任意两个任务都必须“有先后”（称为“可比”）。调度就是要在此基础上生成一个“全序”，即任何两个任务皆“可比”，对任意两个原来就“可比”的任务，新关系与原关系保持一致。换句话说，如果按照这个序号串行执行，一定满足原来要求的依赖关系。这个问题被称为“拓扑排序”问题。读者应该注意到，如果只要解决拓扑排序问题，我们并不需要考虑上述例子中每项子任务的耗时。

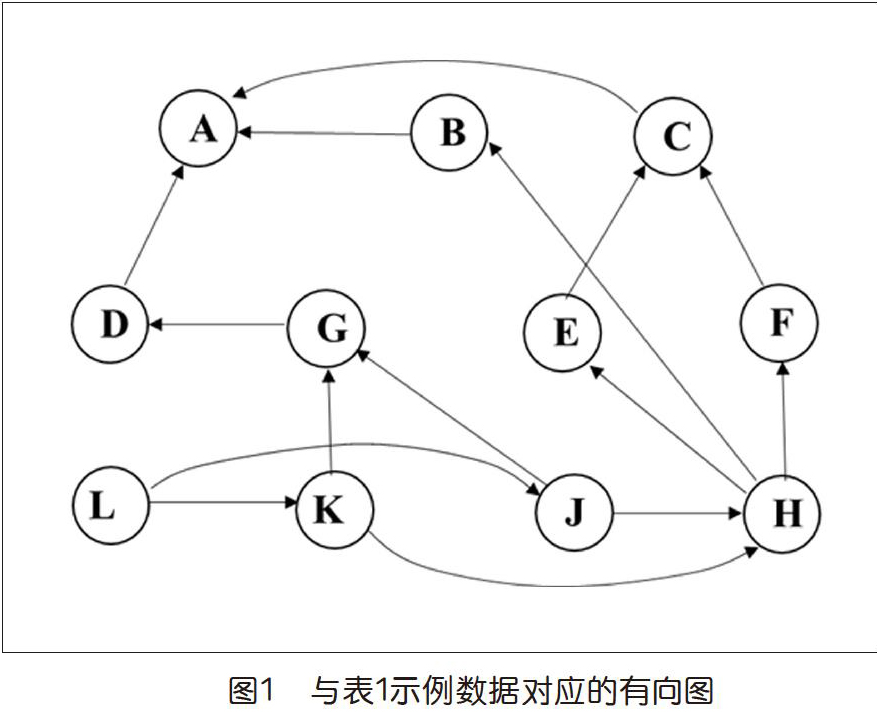
    我们可以建立一个有向图模型。图中每个节点表示一个任务，节点X和Y之间存在从X到Y的有向边（X→Y）当且仅当对应的任务X直接依赖于任务Y。上述例子的图模型如下页图1所示。图中节点名称采用表1中的任务名称。我们暂时不考虑任务的耗时。

    在这个模型上解决拓扑排序问题的思路非常简单。我们要给每个节点分配一个序号，这需要遍历所有节点。根据问题要求，如果任务X依赖任务Y（无论是直接还是间接），分配给节点X的序号必须大于Y的序号。在图模型中存在的任意一个简单有向通路v1，v2，…，vk表明任务i-1依赖任务i（1

    图节点遍历常用算法有两种：深度优先与广度优先。我们在本系列文章中前面讨论走迷宫算法时介绍过深度优先算法（DFS）。它的基本步骤如下（这里假设从起始点一定可通达所有节点）：①选择一个起始点，并将其作为第一个“当前节点”，设置状态为“已访问”。②如果当前节点所有的相邻节点都是“已访问”状态，结束从当前节点开始的遍历子过程，退出（回溯）。如果当前节点就是起始点，则整个遍历完成。③取当前节点相邻节点中的一个尚未访问过的节点w作为新的“当前节点”，设置状态为“已访问”，从w开始递归执行本过程（即上述第2步）。

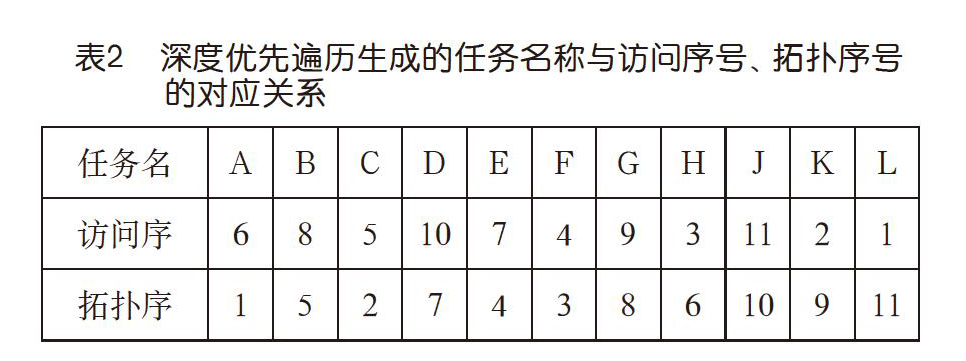
    在图1中从L开始执行深度优先搜索过程，可能产生的一个访问序列如下：L，K，H，F，C，A（A，回溯）（C，回溯）（F，回溯）（H），E（E，回溯）（H），B（B，回溯）（H，回溯）（K），G，D（D，回溯）（G，回溯）（K回溯）（L），J（J回溯）（L，结束）。它对应表2中的“访问序”。具体的访问序列与当前节点的所有相邻节点被访问的次序有关（由算法实现决定，即上述算法第3步节点w的选取）。这对后面生成的全序有影响，但对满足问题的约束条件没有影响。

    下面来看“拓扑序”的确定。在深度优先搜索过程中，任一节点在回溯后就再也不会被访问了，也就是它所依赖的节点都已经访问过了，因此如果我们在其即将回溯前给它分配拓扑序号，且号码值从1开始依次加1，则上述过程给出的拓扑序号与任务名称的对应关系如表2中的第三行所示。读者容易验证这个次序满足表1中的任务依赖要求，即按照这个序号，先做“1”（A），后做“2”（C），……，最后做“11”（L），就不会出现当要做一件事的时候，它前面还有该做没做的事情。

    对前述深度优先算法稍加修改（在回溯前给节点编号），即可得一个拓扑排序算法（留作读者练习）。其中有两点值得注意：第一，起始节点（将最后编号）应该是不被任何其他节点依赖的，即要选入度为0的节点;第二，对于任意的依赖关系输入，拓扑排序问题未必都有解。设想一下，有两个任务X和Y，X依赖于Y，但Y也依赖于X（可能是间接的），这就形成了所谓相互依赖的“死循环”，无论怎么安排都没法满足它们。这种状况在图1所示的图模型中体现为一条有向回路。在算法中判断这种情况的标准方法是用3个状态（通常形象地用顏色白、灰、黑标记）来表征一个节点在深度优先搜索过程中不同时间段上的情况。White表示“尚未发现”，grey表示“已发现但还未关闭”（在进入DFS时设置），black表示“已关闭”（即已回溯，在离开DFS时设置）。在第2步，发现了一个灰色节点，就意味着图中存在回路（读者可想想其中的道理）。

    这个算法只是在深度优先搜索过程中增加了常数次简单赋值操作，所以其时间代价与深度优先搜索算法一样，为O（m+n），其中m与n分别是输入图的边数与节点数。

    对于不熟悉深度优先等递归性质算法的读者，还可以有一个概念上较简单，但时间代价较大一些的拓扑排序算法。其要点是：不断删去有向图中出度为0的节点。删除的顺序就是节点的拓扑序。这种思路的程序实现十分容易，直接操作邻接矩阵就可以，不用递归，对初学者有一定教益。

    ● 执行时间与依赖关系共同约束下的任务调度

    现在我们来考虑任务执行时间的影响。将表1给出的例子画出反向依赖图，并将每个子任务的耗时标注在指向相应节点的边上，我们就得到图2。此时，边A→B的含义是“B必须在A做完了后才可以开始”（即B依赖于A），上面的“30”表示B需要耗时30分钟。显然，边上的数据标在箭头末端的节点上也是可以的。

    这样一个任务关系图中显示了在人力允许的情况下可以并行执行的多条路径，如在任务A完成后，可以同时执行{任务B}以及{任务C，任务E}，甚至还能同时执行{任务D，任务G}（大括号内的任务串行执行）。图中粗线显示，到整个项目执行完成最长的一条路径是A→C→F→H→J→L（图中用粗线表示）。这条路径耗时130分钟。如果不能压缩这条路上的耗时，其他任务即使压缩了耗时也不能将整个项目的完成时间提前。因此，这条路径称为“关键路径”，关键路径中体现的依赖关系称为“关键依赖”。在这个例子中，单项任务耗时最多的是包饺子（G，80分钟）。增加一些人手可以将其耗时降下来。但它并不在关键路径上，因此包饺子提前完成对于整个项目缩短时间并没有任何意义，只是增加了一些闲着等待的人。

    此时，调度的追求是识别关键路径，从而得知完成整个工作所需时间的下界。在任务管理中，找出关键路径，并通过有针对性地加大资源投入、改进技术等手段压缩该路径上的耗时，是提高办事效率的重要方法。

    基于前述深度优先搜索算法，适当记录中间结果，就可以解决这种关键路径问题。它包括两个方面，一是关键路径的长度（时间），二是路径本身（经过的节点）。在这个意义上，和上一期讨论的“投资组合问题”有共通之处，即不仅要得到一个目标量值，还要得到构成该目标量值的具体实现。这也是计算机问题求解中的一种相当广泛的要求，策略大都是通过在追求目标量值的过程中记录某些中间结果，然后通过它们反演出具体实现方案。下面来看怎么解决这个问题。

    这里的关键是要认识到，如果任务A直接依赖任务B，则A的最早“开始时间”不可能早于B的最早“完成时间”。进而，若A依赖多个任务，则A的“开始时间”不可能早于它们“完成时间”的最晚者。而一个节点的完成时间等于它的开始时间加上它的耗时。

    这样，参照图2，如果我们确定了每个节点的最早“完成时间”，对应最后一个任务（L）的，就是关键路径的长度。而在L所依赖的节点中，谁的完成时间最晚，也就是关键路径上的前一个节点。如此继续，直到起始节点A，就反演出了关键路径的构成。鉴于实现这种思路的程序不长，下面我们将基于图3中的可执行Python函数予以解释。

    其中用到的几个数据结构是——①neighbor：线性表向量，初化为每个节点的出向邻居，基于图1（而不是图2）的方向性;②delay：向量，输入数据，记录每个节点的耗时;③visited：向量，记录节点在深度优先过程中是否被访问过，初始化为全False;④finished_time：向量，记录节点的最早完成时间;⑤critical_dependance：向量，记录关键依赖关系。

    看这段程序，如果没有行2，8～10，14～17，那就是一个从current_node（当前节点）开始的标准深度优先搜索。其中第4行的for语句保证当前节点的每一个依赖关系（x）都会被考虑到。9～10，14～16行就是我们说的记录中间数据。站在当前节点的角度，把所依赖节点的完成时间的最大者定为自己的开始时间（my_starting_time），同时也在critical_dependance中记下它。最后再加上自己的耗时，得到自己的完成时间，供依赖自己的节点后续参考。

    这其中有两点值得注意，一是为什么要考虑当前节点的所有依赖节点，而不仅是刚看到的white节点？这是因为前面说的，当前节点的最早开始时间不得早于所依赖节点的最晚结束时间，与访问顺序无关。二是在最后的critical_dependence中，不仅记录了从开始任务到结束任务的关键路径信息，还记录了从开始任务到任何任务的关键路径信息。基于图3的程序，运行前面的例子，结果如表3所示。

    从中，我们可以反演出整个任务图的关键路径：A→C→F→H→J→L。

    从上述讨论中能看出，这个算法只是根据特定问题的需要，在深度优先搜索算法中加入适当代码保留一些中间数据，就实现了我们期望的问题求解目标。这样，我们就能够将DFS过程当作一个“算法框架”，可以用它拓展出针对不同问题的许多算法。

    关于关键路径问题的求解，最后需要提请读者注意的是，它所面对的图不仅应该是有一个有向无环图，还应该是有唯一“起始节点”（入度为0）和唯一“结束节点”（出度为0）。每个节点都可达结束节点，都可被起始节点到达。为此，在实际应用中有时需要添加虚拟的起始节点和结束节点，算法方可正确运行。

    ● 负载均衡调度问题

    本文开始就提到调度问题最大的应用背景应该是生产活动，具体应用与限制条件的不同发展出了大量的调度问题，与我们前面的拓扑排序问题有很大差别，生产实践中产生的调度问题大多属于“难”问题。对于计算机科学家而言，“难”问题通常指这样的问题：问题输入规模增加到足够大时，我们倾向于相信全世界的计算资源都不足以支撑我们获得问题的最优解。但调度问题的解往往涉及巨大的经济效益，这就促使人们设法寻求可接受的解决途径。放弃对最优解的追求，转而满足于质量有一定保证的近似解就是目前遵循的最重要的途径之一。令人惊喜的是，这往往会带来非常简单但可以满足实践需要的算法。下面用一个最容易表述的例子来让读者形成一些初步的认识。

    考虑需要在m台完全相同的机器上执行n项没有依赖关系的任务，pi（i=1，2，…，n）为任务i的耗时，在任何一台机器上执行都一样。假设每项任务不可分割，如何将n项任务分配给m台机器，使得项目总执行时间最短？这个问题称为“（多台相同机器上的）工期问题”。稍微想一想，不难认识到这里就是要追求让n个任务尽量“均匀地”（以时间为衡量）在m台机器上分配，而最優解不可能小于S=∑ipi/m。

    显然，如果机器数m大于等于任务数n，因为任务不可分割，则最大任务耗时就是整个项目最小完成时间。我们下面约定n>m。可以证明工期问题是上面所说的“难”问题。按照最直观的贪心策略我们就可以找到一个结果“可控”的近似算法。

    一个自然的想法是：先把m个最大的任务安排给每台机器，剩下来的再逐个往不同的机器上“塞”。“塞”的原则很简单，当前哪台机器负载最小（即完成已分配任务所需的时间最短）就给它加任务。为此，我们先对所有任务按时间降序排序[时间复杂度为O（nlogn）]，然后一一安排。整个算法过程如图4所示。其中的关键数据包括：①一组集合Ti，1≤i≤m，Ti的元素为已分配给第i台机器的任务下标，算法终止时输出Ti;②数组Time：Time[i]的值为第i台机器当前总负载，算法终止时，Time[i]（i=1，2，…，m）的最大值即为算法计算的结果。

    强烈建议读者用自己熟悉的语言实现这个算法，特别是用尽可能简单的方法实现其中“找出负载最小的机器”。作为一个例子，假设n=10，m=3，任务的负载为80，40，40，30，30，20，20，10，10，5。按照算法，运行结果如表4所示。

    前面我们说这个近似算法是“可控”的，这是什么意思呢？我们希望确定算法的输出与最优解差距有多大？这似乎提出一个“悖论”：如果我们知道最优解，根本不必费心去找近似解;但如果不知道最优解，怎么能知道差距有多大呢？奥妙在于利用数学知识与算法本身的特性，我们可以试图估计出差距的“上界”。这个问题是求最小值问题，因此算法输出的近似解一定大于最优解。如果能确定“最坏情况下”大多少，使用者心中就“有底了”。

    这里的关键在于能否估计最优解的值的“下界”，即最优解至少得多大。前面已经提到，最优解不可能小于均值S=∑ipi/m，即它就是一个下界。

    现在来考虑算法本身的行为。假设整个项目中最迟完成的任务下标为k，则安排任务k时的场景示意如图5所示。

    假定任务k被分配给机器l，则当时机器l是负载最小的，因此Time[l]一定不大于前面k-1个已安排任务的平均耗时。而这只是所有任务中的一部分，所以一定不大于∑ipi/m，因此也不大于最优解。考虑到pk是最小的负载，因此不可能大于平均值（最优解的下界），算法输出的值，就是这两项的和，一定不大于最优解的2倍。在表4所示的例子中，总时间为80+40+40+30+30+20+20+10+10+5=285，因而在3台机器并行条件下，最短时间不会少于285/3=95。刚才的结果是max（100，95，90）=100，相当不错了。

    这种保证得到的解不大于最优解2倍的算法也称为2-近似算法。至于实际应用场景能否容忍这样的误差就得由用户自己决定了。采用更复杂的技术可以进一步降低工期问题算法的误差，甚至可以做到“任意小”（当然效率成本会迅速提高）。

    参考文献：

    [1]Sara Baase.计算机算法——设计与分析导论（第3版）[M].北京：高等教育出版社，2001.

    [2]Juraj Hromkovic.Algorithmics for Hard Problems（2nd ed）[M].Berlin：Springer-Verlag， 2004.

    [3]陳道蓄.迷宫问题中的算法[J].中小学教材教学，2019（10）：76-80.

    注：作者系南京大学软件学院原院长，计算机系原系主任。