投资组合问题

    李晓明

    

    

    

    人们常常讲，要合理分配时间，合理分配资金等。抽象来看，说的都是要将某种掌握的资源，分配投入到某些事项上，希望得到最好的综合回报。这类追求很有意义，因而得到人们的广泛研究。同时这种事情也很复杂，到目前为止并没有一个普适的方案。其复杂性体现在几个方面：第一，每一个可投入的事项（如股票）能得到多少回报，常常并不是事先能够明确的;第二，回报不一定就是金钱，而其他方面（如愉快）常常很难量化，因而难以评估;第三，情势是动态变化的，还有机会成本的问题，今天决定投入（如时间）某事项了，就意味着明天可能难以改投更有意义的事项。

    我们这里讨论一种相对单纯（但并不一定简单）的情境，看算法能怎么发挥作用。

    考虑一定量的资金n，要分配投入到m个不同的项目上，以获得最大的回报。假设在每个项目上的投入和回报的对应关系是预先知道的（如银行定期存款的利息）。下面是一个具体的例子，假设你有n=5万元钱，可以安排在m=3个项目上，表1给出不同的投资量分别可产生的回报。

    你面对的问题就是，如何将5万元钱分配到这3个项目上，让总的回报最大。例如，若你把5万元都投在项目1上，得到回报9，而你在项目1上投4万，项目3上投1万，得到回报7+3=10，就要好一些。是不是还有更好的呢？一般的问题就是，给定任意一个这样的投资回报表，能否有一个系统化的方法（算法），求出最大回报，以及对应最大回报的“投资组合”。

    我们将从问题定义、求解思路、算法描述、算例分析和算法性质这五个方面展开对这个问题的讨论。这也是从算法角度进行问题求解通常要考虑的几个方面。

    问题定义

    给定总投资量n（整数）和m个单增项目回报函数[注]，fk（），k=1，2，…，m，要把n分成m份（整数），n1，n2，…，nm，其中nk≥0，满足：

    能够看到，问题定义中强调了整数（按照问题背景，我们应该理解为非负整数）和回报函数的单调性（严格讲非减就可以了）。前者可以说主要是为了让讨论比较简单，后者不仅是因为具有一般意义下的合理性，对算法设计的考虑也有某种关键性意义，将在算法性质部分看到。

    求解思路

    谈求解思路通常意味着某种方法论，即从哪个视角看待这个问题，入手去解决。下面介绍的，在计算机算法领域被称为“动态规划”的方法，是算法设计的经典技巧之一。

    不妨先看看只有两个项目可投资的情形，即m=2。如何确定最优组合？无非就是要看下面这n+1种可能中哪一个最好：

    注意，所有可能一共是n+1种，而不是n种。还要注意，相关的f1（n-k）和f2（k）都是已知的，即投资回报表给出的，于是我们有充分的基础数据来用以得出结果。让我们把这一结果记为F2（n）=max{f2（k）+f1（n-k），k=0，1，2…，n}，即两个项目最优投资组合的回报值。

    如果有三个项目（m=3）的机会呢？那就可以看是否能通过给第三个项目也分配一些资金（k），剩下的（n-k）还是在前两个项目中按照最优的方式分，可以获得更高的回报。如果用F2（n-k）表示投资量n-k在前两个项目上分配能获得的最大回报，也就是要看（注意f和F的区别）：

    这n+1种情况中哪个最好？而其中的每一个F2（n-k）是我们已知怎么求的，即令式（2）中的n为这里的n-k。

    这种想法可以推广！一般地，用Fi-1（x）表示在i-1个项目上投资x的最优回报，在i个项目上投资x的最优回报Fi（x）就是下面x+1种可能中的最大值，fi（k）+Fi-1（x-k），k=0，1，2，…，x，记为：

    其中，fi（k）是事先给定已知的。如何得知Fi-1（x-k）呢？这里呈现出一种“递归定义”的特征。我们可以想象将Fi-1（x-k）进一步展开，直到i=2，Fi-1（x-k）=F1（x-k）

    =f1（x-k），也就是已知的。

    在具体计算的时候，则是反过来——自底向上，从i=2开始，先算F2（x），x=0，1，…，n，再算F3（x），x=0，1，…，n，等等，直到Fm（n），就得到了我们要的结果。这里的要点是这些自底向上计算的中间结果过程Fi（x）都被记录下来，直接用在后面的计算过程中，从而免去大量重复计算的开销。

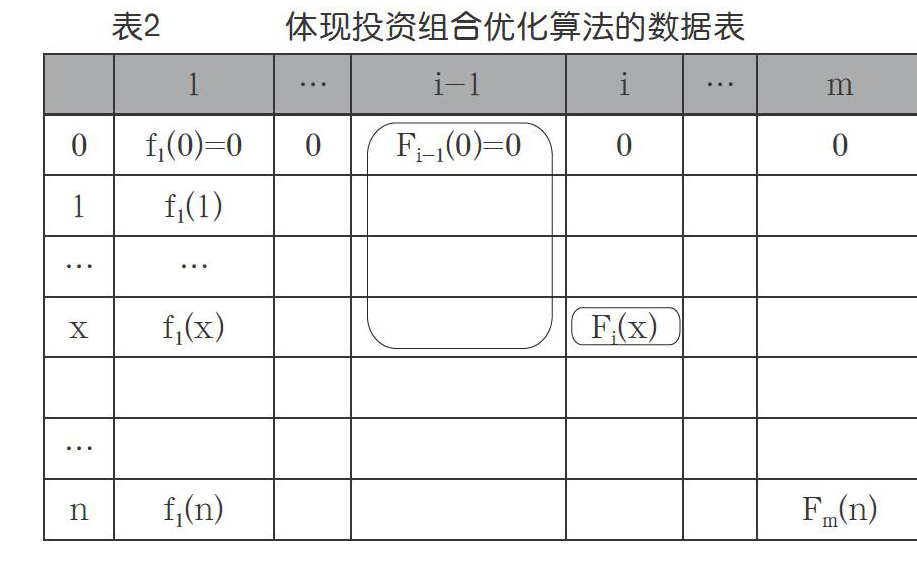
    仔细体会上述过程，我们可以形象地感到是在从左到右填一张（n+1）行m列的表，表中要填的值就是Fi（x），x=0，1，2，…，n;i=1，2，…，m。当计算Fi（x）的时候，要用到相应单元的左邻列的上半部单元的值，即Fi-1（0），Fi-1（1），…Fi-1（x），如上页表2中的指示框，还要用到式（4）中指出的fi（）。

    这也就是“动态规划”方法的基本风格，不少优化问题的求解步骤都可以归纳为这个样子，要领就是要从左到右、从上到下“填一张二维表”。表填完了，所需的结果就出现在表的右下角单元中。当然，能这么做成功的条件是表最左边的列和最上面的行的数据是已知的，也就是所謂“边界条件”。

    上述讨论，指出了Fm（n），也就是表2右下角单元值的计算过程。这是否就完整解决了我们最初提的问题呢？还没有！我们要的不仅是最大可能的回报值，还要一个具体的投资分配方案，它取得的回报是Fm（n）。如果只是算得一个数值Fm（n），具体该怎么投资还是不清楚。

    这里涉及用算法来解决优化方案设计中常见的一个挑战。通常，问题的目标是要得到一个优化的设计，而不仅是表示设计优化的量值。这就好比用导航软件，仅仅告诉从A到B的最短路径是10公里还不够，我需要的是告诉我如何走，最后是10公里。

    对于这样的需求，通常可在求得最优值的过程中记录一些关键性中间结果来满足。那些中间结果帮助我们回过头来构建具体的优化方案。对于本文讨论的投资组合问题，如果在上述计算Fi（x）直到Fm（n）的过程中同时也记住形成Fi（x）时对应在fi（）中的投资量，也就是在式（4）中取得最大值的k，就能够让我们在算出Fm（n）后逐步“回溯”得到对应的投资方案。也就是说，在算法具体实施中我们面对的是如下页表3所示的情境。与前面的表2相比，就是在每个Fi（x）旁伴随了一个在项目i上的投资量K，它是0到x之中的一个数。该投资量是与投资项目i和当前总投资量x相关的，我们用Ki（x）表示。算法实现中可以定义一个与Fi（x）结构相同的数据结构存放Ki（x），或将原来的表格每一列扩展为两列，分别存放Fi（x）和Ki（x），表3即为一个示意。其中每个数据单元中有两个数[Fi（x），Ki（x）]。

    这里，我们首先能认识到的是，这样的Ki（x）在按照式（4）计算Fi（x）的过程中“顺手”就可以得到了，即对应那个最大值的k。如何利用它们来构造对应Fm（n）的投资方案，将在下面的算法和例子中介绍。

    算法描述

    如前所述，对这种投资组合问题，算法分为两个阶段。第一阶段是算得最终的优化值，同时记住必要的中间结果;第二阶段是基于第一阶段的结果，构造一个具体的优化投资方案。于是我们的算法也分成如下两段描述。

    第一段是计算最优回报，如上页图1所示;第二段是计算最优组合，如上页图2所示。

    第一段的第1、2行初始化Fi（0）=0，F1（x）=f1（x）， K1（x）=x，i=1，2…m;x=0，1…n，也就是那个二维表的第一列和第一行。随后从左到右、从上到下逐个计算Fi（x）、Ki（x）。涉及三重循环，第一重循环投资项目数i从2到m，第二重循环总投资量x自1到n，第三重循环中k为投入到项目i的总量。计算Fi（x）需要从x+1个fi（k）+Fi-1（x-k）值中取最大的，对应在项目i上的投资量k值存入Ki（x）。

    算例分析

    為了更好地说明问题，我们看一个稍微大一点的例子（取自参考文献1），n=5，m=4。4个项目的回报函数（fi（x））如表4所示。

    基于表4，运行上述第一个算法（计算最优投资回报），得到如表5所示的结果。

    作为一个例子，我们来看对应在前两个项目上投资5的结果“F2（5）=26，K2（5）=4”是怎么得到的。为了得到F2（5），也就是要看在F1的基础上，在第二个项目上的不同投资量会怎样，即比较下面6个数：

    其中26是最大的，而此时在第二个项目上投入4，即K2（5）=4。

    我们看到，这个例子的最佳回报是61。如何能得到具体的投资方案呢？这就是上面第二阶段算法（计算最优组合）的作用。它做的是一个“倒推”。从最后的结果（61，1）中的1开始，它意味着要在项目4上投入1，于是在其他三个项目上的投资量就是5-1=4，其中分配在项目3上的投资量是K3（4）=3。那么在其他两个项目的投资4-3=1，继续回溯K2（1），为0，意味着在项目2投资为0。继续回溯K1（1）=1，那么对应项目1的投入是1万。结论就是，给项目1投1万，项目2不投，项目3投3万，项目4投1万，就能得到最高回报61。

    算法性质

    我们关心正确性和效率两个方面。

    （1）这是一个正确的算法吗？我们关心两点，一是为什么算法结束时给出的Fm（n）的确就是在m个项目上投入n万元的最优投资组合的回报，即最大回报，二是为什么从记录了[Fi（x），Ki（x）]的表中，结合给定数据fi（x），x=0，1，…，n;i=1，2，…，m，就能倒推出一种最优投资组合。

    对于第一点，关键是认定公式（4）的正确性。可以这样推理，即任何在i个项目上投资x的最优组合，总可以表达为：

    （5）其中ki=x。由于Fi（x）是最优的，这个式子右边的前i-1项加起来就必须是Fi-1（x-ki），即在i-1个项目上安排投资量x-ki能获得的最佳回报，也就是Fi（x）=Fi-1（x-ki）+f（ki）。式（4）无非是说，既然Fi（x）一定是这个形式，那就看看所有这种表达式中哪一个取得最大值，我们就取它做Fi（x）！有了这个认识再看算法，无非就是保证在按照式（4）计算每一个Fi（x）的时候，所需要的数据都已经在前面准备好了。表2数据项的填写，按照从左到右、从上往下的次序来完成，就保证了这一点。

    对于第二点，注意算法是从总投资量开始，倒序看应该给每个项目安排多少资金。因为在第i列记住了Ki（x），于是就知道了该给项目i安排的投资量。而从当前投资量x中减去Ki（x），就是给前面i-1个项目安排的投资量。据此就可以定位到表中第i-1列的适当的行，这就是从Ki倒推回Ki-1的根据。这个过程从i=m，x=n开始，直到i=2。在各项目上的投资量，就是一路上确定的那些K。算法正是这么做的。

    这里，关于算法的第一阶段有两个进一步的问题提请细心的读者注意：第一是项目的顺序，我们一直说“第一个项目”“前两个项目”等，那么哪个项目算是第一个、第二个在此重要吗？仔细体会上述式（5），会发现无关紧要。任何顺序都会得到同样的最终结果Fm（n），尽管中间的Fi（x）可能不一样。第二是关于式（5）的条件中有“ki=x”。这意味着为了得到最大回报，一定要用完所有的投资。如果没有回报函数单调增的假设，这还真不一定。

    （2）这个算法的效率如何呢？注意到整个过程就是要计算Fi（x），i=2，3，…，m;x=1，2，…，n，即n行m-1列。而计算一个Fi（x）需要做x+1次比较，也就是说，计算一列数，Fi（x），x=1，2，…，n，计算量为n（n+1）/2，于是整个计算复杂性就是O（m*n2/2）。

    此时，比较一下蛮力法的效率会有意义。即根据问题的定义，给定正整数n，要把它分成m个非负整数，n1，n2，…，nm，nk≥0，满足：

    且要基于各个项目的回报函数，fi（），最大化总回报：

    蛮力法就是枚举每一个满足（6）的解，带入（7）得到对应的值，留下最大的。这其中的计算量，正比于等式（6）的可行解的个数。组合数学告诉我们，它等于，大多数情况下要比m*n2/2大很多。