互联网+模式下共享试题的评价设计

    李小号 孙少妮 赵薇 赵群超

    

    

    

    摘? 要 讨论机械制图类课程在“互联网+”模式下的跨校使用及考核评价环节出现的问题，以机械制图类课程为例，分析学生课程学习效果的考核评定方法及模式，为建设发展适应共享机制的该课程教学资源提供参考意见，可在一定程度上提高院校间的该课程教学资源的利用效率及评价质量，对同类课程资源有机结合以及共享发展提供借鉴。

    关键词 机械制图;互联网+;共享试题;试卷评价体系

    1 以东北大学机械制图课程为例的考核成绩分布分析

    以东北大学机械类专业技术基礎课机械制图课程2018年试卷及成绩数据为依托，统计讨论该类课程跨校共享修读的质量评价方法。

    从2018年学生学习数据库中抽取共享学习该课程的300名学生作为样本数据。对大部分成绩统计而言，要是教学质量和学生考试成绩符合教学常规，基于数理统计中的林德贝尔格—莱纬中心极限定理[1]可知，学生的总体成绩应接近正态分布，一般出题会尽量考虑使成绩呈现正偏态分布模式，以期比例更大的学生能进入合格线内，并有一定的区分度。

    先假设东北大学2018年建立的共享机械类试题考试总体成绩符合正态分布，从300份共享答卷中提取样本容量为n（本文分析时取n=300）。

    设选取样本试卷中学生个体总成绩为xi（i=1，2，…，n），则样本均值与样本标准差S分别为：

    为检验考生成绩分布的正态性，采用上述样本成绩均值及成绩样本标准差S为抽取成绩样本的总体均值μ和标准差σ的估计[2]。通过如下步骤检验前述假设正确性。

    1）将n个样本成绩划分成k个计算区间。本文分析时将成绩分值按0～35、36～50、51～60、61～70、71～80、81～90、91～100划分成七个计算区间。

    2）将成绩样本个体处于上述七个区间的事件定义为E1，E2，…，E7，如果前述试卷考试成绩呈正态分布的假设成立，则可计算出E1～E7事件在七个划分区间的发生理论频数fj，其中fj=f（Ej）（j=1，2，…，7）。分析的样本试卷在七个划分区间的实际频数为，其中Pj为事件Ej的实际发生数，n为抽样试卷总数。

    3）根据统计理论[1-2]，如果前述试卷成绩分布假设成立，样本试卷实际频数与理论发生频数差异值应在统计分析设定的临界范围内，且符合皮尔逊定理[2];如果差异值超出临界范围，则认为正态分布假设不成立。检验实际发生频数和理论发生频数，其统计量X2应近似服从式（3）给出的χ2分布规律：

    在分析共享测试卷各考题是否符合期望的近似正态分布情况时，学生个体各道考题的得分必然是呈现起伏波动的。本文通过式（4）计算样本试卷中每个应试学生各题的考试得分值与该题样本成绩得分均值的差的平方和，进而得到试卷各题标准差，表征学生解答该题的成绩波动程度。

    抽样的2018年共享试卷中共设置有七道测试题，按试题难度系数类型划分为三类（难度系数计算详见本文第二部分），选取第一题（难度：较易）、第三题（难度：一般）、第六题（难度：较难）计算各题的正态分布检验，见图1。

    由图1可知，抽样试卷各道考题成绩分布均服从或近似服从正态分布，且除第六题外均属于正偏态分布（如图1a、图1b所示，其中图1a反映的第一题因难度“较易”，学生得分较理想，与本文第二部分分析吻合），偏度均值为0.381;第六题由于难度系数较高，学生该题得分稍低，显现出负偏态分布特性（负偏态值为-0.113）。成绩的正态分布性也反映了试题的知识点全面，试题难度为适中偏易，符合该测试卷对学生进行学习达成检验并有一定区分度的目标。

    2 以东北大学机械制图课程为例设置的试卷评价体系指标

    现行的各类课程成绩分析、试卷分析惯用的方法是将学生的试卷考试成绩进行定量化，在设定的定量化指标上，综合教师教学工作、学生学习过程等环节，二次开展定性评估，最后综合评定授课效果、学生学习效果以及试卷考核效果。查阅《教育统计学》[3]等文献，现行的主要定量评价指标多采用试卷教学内容覆盖度、难度、信度、效度、区分度等指标。根据需要，本文采用的指标中偏重覆盖度、难度和信度指标，综合评估共享使用的考核考试是否有效地检测学生的学习情况。

    试卷覆盖度R分析? 机械制图课程内容可供考核的知识点很多，怎样评判试卷考核尽可能地覆盖较大知识面，反映学生更接近真实的知识点掌握水平？这就需要对试卷出题的覆盖度进行分析。在课程内容知识点总量保持一定的情况下，试卷中各题之间的离散性越大，则该试卷所考查知识点的重叠性越低，即所囊括的知识点越多。本文采用统计学[1]中的相关系数Rij进行覆盖度R的间接评价并进行描述，如式（5）所示：

    式中，n为成绩样本总数，yqi为第q个学生的第i题得分值，yqj为第q个学生的第j题得分值，为第i题样本成绩得分均值，为第j题样本成绩得分均值，σi为第i题样本成绩得分值标准差，σj为第j题样本成绩得分值标准差。

    通常为提高试卷覆盖度[3]，要求Rij<0.2。在各题相关系数Rij基础上，可用试卷上各题的相关系数加权平均[1-2]计算该共享试卷的总体覆盖度R，即：

    基于2018年抽样试卷数据，依据式（5）计算该共享试卷覆盖度Rij数值见表1。

    基于表1计算的各题交叉相关系数，利用式（6）可计算本共享测试卷的总体覆盖度R=0.819，表明该测试卷总体覆盖度良好[3]。

    试卷难度分析? 试卷难度即考试出题的难易程度，是评价试题质量和学生掌握知识点水平的重要量化指标之一。综合考虑试题中各题考查知识点的难易及学生学习能力，在评估计算试卷的难度系数时，采用样本试卷中各题的平均得分率占比进行量化，设置第i考题的难度系数Pi计算公式如式（7）所示：

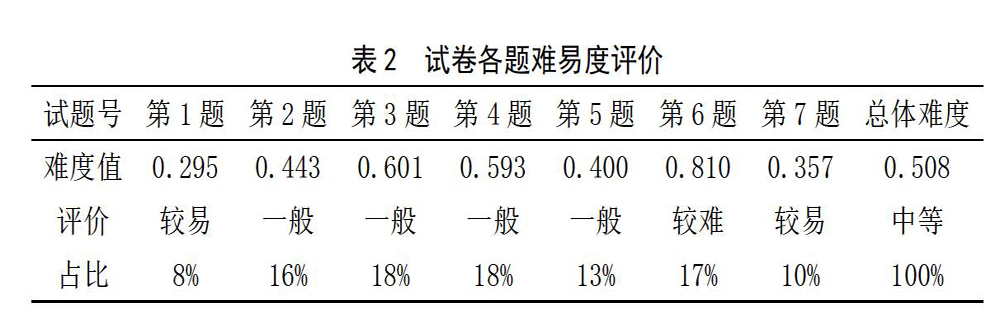
    式中，vij为样本试卷中第j考生的第i考题得分分值，Vi为样本试卷第i考题的满分值，n为样本试卷总数。由式（7）知，Pi位于0～1之间，如果Pi=0，则表明该考题全部回答正确，该道考题出题简单，难度系数低;而若Pi=1，则表明该考题全部解题错误，该道考题出题过难，难度系数太大，从考核角度来看，此题出题意义较小。对抽样的试卷中全部七道题进行难易度分析，得到表2结果。

    由表2可知，第1题、第7题难度系数较低，属于较易题型，该类难度题占总分比为18%。统计从共享测试卷中抽样的300份试卷也可看出，第1题平均得分为7.3分，标准差为3.014;第7题平均得分达9.0分，标准差为2.781，表明参与应试学生该类“较易”题完成得都很好。

    统计试卷中难度设置“一般”类题型包括第2题、第3题、第4题及第5题，该四道题分配题分占比达到60%，属于学生想达到检验合格水平必须较好完成的内容。由表2可知，该类题难度系数从0.400～0.601，表明想全部拿分还是有一定困难的。统计抽样试卷可看出，这四道题平均得分在57.89分，单看平均得分还是比较满意的;但计算这四题得分标准差可以发现，S=5.619，表明学生“一般”难度题型得分离散程度较高，两极化相对比较严重。

    第6题属于有一定难度的拔高题型，难度系数为0.810，得分均值12.07，标准差S=6.106。从得分和标准差统计来看，该题学生测试情况满足出题预想，实现了既让好学生能有所突出表现，又让大多数学生能有所得。

    综合评价该试卷来看，该共享测试卷整体难度“一般”，符合课程学习检验性考核的目标。

    试卷信度分析? 试卷的信度是指该试卷的可靠性和稳定性的程度。一般认为，将同一份测试卷对同一组应试者进行多次反复测验，所得结果一致，则该测试卷具有很高的信度。通常，评估试卷信度r指标采用如式（8）所示的克伦巴赫法[2]进行量化计算：

    在式（8）中，N为该套共享试卷中试题总数，σi2为试卷中第i题学生得分值的方差，σ2为学生整份试卷得分值的方差。

    在实际试卷信度分析中，参与测试的学生的真实分值与误差分值是不可知的，为对信度进行量化和检验，多采用分半法实施。所谓分半法，就是将考生的测验成绩划分为两部分，模拟近似于两次对学生进行平行测验或看作一份试卷实施了可对比的两次测试。比较简单可行的方式就是将试卷中的考题按题号的奇偶分为两半，然后计算两半成绩的相关系数Rij作为信度系数。此处i是奇数题号划分的部分，j是偶数题号划分的部分。一般认为信度系数r>0.6时[3]，该试卷的检测功能是稳定可信的。

    计算抽样试卷各题方差，利用式（8）计算试卷信度为0.612，符合文献[3]设置阈值，可认为该共享的2018年测试卷结果是合理可信的。但在共享试卷的实际测试操作中，由于现行的处理方式是组织学生网上答题，虽然给各位考生规定了考试规则和答题时间限制等一系列规定，但由于网络答题操作对学生诸如考试地点等没有硬性要求，难免出现分享答案、相互参考答案等需要改进的现象，因此，试卷的可信度分析还有待进一步研究改进措施。

    3 结语

    通过文中基于“互联网+”共享模式的试卷评价模型，并对东北大学2018级学生机械制图课程考核试卷质量分析，验证和解释了文中研究成果和方法的合理性与有效性，结合分析结论和近年该课程共享考核操作模式，检验了该课程共享考核成绩的正态分布性。本文共享试题覆盖度为0.819，符合0.75～0.9良好范围;难度控制在0.508，满足0.35～0.8中等难度范围，且照顾到参与共享学习高校学生基础差异，难度取值应适当偏小;信度控制在0.612，大于0.6设置的可信阈值;且课程考核定位为检验性考试，成绩分布为以正偏态分布的试卷为理想期望。

    本文分析表明，用数理统计方法對考试结果进行统计分析，可以促使任课教师总体把握课程的考试情况与教学情况、学生课程的学习效果等，并为教学评估提供理论依据和统计数据支撑，分析方法和结果可为今后该课程的共享建设及考核命题工作提供参考依据。

    参考文献

    [1]茆诗松，吕晓玲.数理统计学[M].2版.北京：中国人民大学出版社，2016.

    [2]Hogg R V， Craig A T. Introduction to Mathematical Statistics[M].5th Edition.高等教育出版社，2007.

    [3]赵必华，王孝玲.教育统计学[M].北京：北京师范大学出版社，2008.