例谈函数方程思想的教学策略

    宫明

    

    

    

    [摘? 要] 函数思想与方程思想之间是密切相关、相辅相成的，函数与方程之间的辩证关系，形成了函数方程思想. 中考复习中，进行函数方程思想的专题讲解，对帮助学生提高函数方程思维品质有着很重要的意义.

    [关键词] 函数;方程;函数方程思想;教学策略;中考复习

    方程与函数相结合的综合题，是各地中考试题的热点题型，主要是从动态角度建立函数解析式，从静态角度建立方程求解，解题时要注意函数的图像信息与方程的代数信息的相互转化. 笔者开设了一节中考复习公开课“函数方程思想的应用”，以函数的本质——“变量”为抓手，注重数形结合思想的渗透，突出函数与方程的灵活转化，为函数方程思想的中考复习提出一些建议.

    从数式方程走出变量函数

    例1? 已知一串数字：-8，-5，0，7， 16，…，按此规律，第______个数是891.

    师：这是一条找规律的题目，同学们小学的时候就接触过，你会做吗？

    生1：我使用搭小桥找规律的方法，数与数之间的间隔分别是+3，+5，+7，+9，…，按此规律，就可以数到891.

    师：你数到答案了吗？

    生1：感觉有些困难.

    师：好，这名同学通过差的方法探讨数量间的规律，能得到答案，但可能要费点时间.

    生2：我发现间隔+3，+5，+7，+9，这与1，4，9，16，25的间隔相同，所以可以把每个数看成1-9，4-9，9-9，16-9，25-9，这样数的规律就可以写成x2-9，当代数式等于891，列方程可解得第30个数为891.

    师：很好，这名同学将原数字与1，4，9，16，25建立联系，找出答案. 有没有同学也使用这种方法？

    ……

    师：这些同学思维很活跃，但如果没有想到这一层联系，这道题目就没有办法解决了吗？

    生3：第1个数等于-8，第2个数等于-5，第3个数等于0……以此类推，出现很多组有序实数对，然后通过列表、描点、连线发现图像是抛物线，使用待定系数法算出二次函数解析式，当y=891时，x=30，也可得到答案为第30个数.

    师：非常好，这名同学从函数角度发现数的规律，然后建立方程解题，他所使用的思想方法就是函数方程思想.

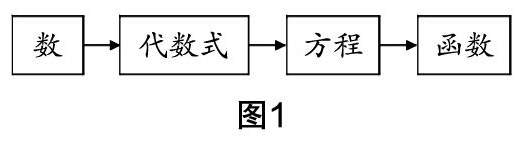
    实施意图? 数学课程标准从三至六年级鼓励学生摆放实物、画图和发现数字变化规律，促进“关系”思想的萌芽;七年级通过用代数式描述数量的变化，搭建起“模式”与“关系”的桥梁;八、九年级通过观察图像，从直观的直线、曲线体会不同的函数. 3名同学对本题的解答，体现了思维的不同层次，由直观、形象到抽象、逻辑，再到问题一般化的过程，经历了如图1所示的环节.

    函数方程思想的重要体现

    例2? 当x=m或x=n（m≠n）时，代数式x2-2ax+a2+4的值相等，则当x=■时，代数式x2-2ax+a2+4的值为______.

    师：请同学们计时完成，比比谁做得更快.

    生1：根据题意，我可以建立等式m2-2am+a2+4=n2-2an+a2+4，解得m+n=2a，即x=a，那么代数式x2-2ax+a2+4的值为4.

    师：你花了多长时间解决这道题？

    生1：我花了2分多钟.

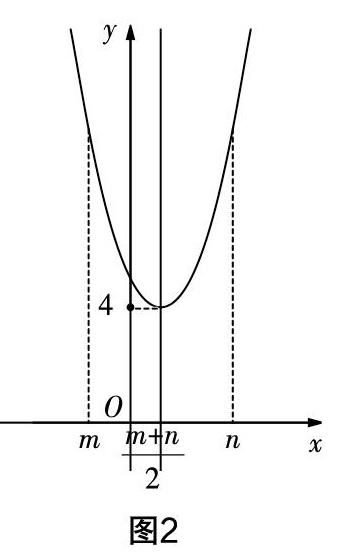
    生2：我把代数式x2-2ax+a2+4理解成二次函数y=x2-2ax+a2+4，顶点式为y=（x-a）2+4，通过抛物线的图像我发现，求当x=■时代数式的值，就是求顶点的纵坐标，看图2可得答案为4.

    师：你花了多长时间呢？

    生2：不到1分钟.

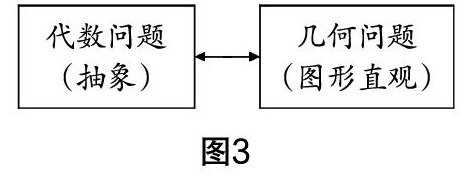
    实施意图? 学生在学习和掌握函数和方程思想时，往往是一个螺旋上升的抽象过程. 抽象的数字往往可借助直观的图像来认识和思考，因此数形结合思想就成为研究函数方程思想的重要工具. 数形结合思想也是笛卡尔数学的重要思想，列方程和建立函数关系的重要思想就是笛卡尔数学思想的运用，其步骤如图3.

    本题对比了2种不同的解题方法，可以发现把代数式理解为函数，借助函数图像，可以使理解更加直观，使解题更加便捷.

    函数思想与方程思想的依赖

    关系

    例3? 关于x的一元二次方程ax2-3x-1=0的两个不相等的实数根都在-1和0之间（不包括-1和0），则a的取值范围是______.

    学生思考3分钟后让学生回答.

    生1：因为一元二次方程ax2-3x-1=0有两个不相等的实数根，我通过根的判别式解得a>-■，之后我就不会了.

    生2：实数根都在-1和0之间，我想先利用公式法解出方程的根，再建立不等式解题，但不等式中有根号，我们没有学过.

    师：这名同学的尝试没有成功，但探索精神值得大家学习. 我们是否可以把方程问题转化为函数问题来思考？

    生3：一元二次方程ax2-3x-1=0的实数根可以看成二次函数y=ax2-3x-1的图像与x轴交点的横坐标.

    生4：我画出抛物线的图像，通过图像可以发现，当x=0时，y<0，即-1<0，当x=-1时，y<0，即a<-2，所以，最终答案是-■

    例4? 如圖5，一次函数y1=x与二次函数y2=ax2+bx+c的图像相交于P，Q两点，则函数y=ax2+（b-1）x+c的图像可能是（? ? ? ）

    师：你是如何思考这道题目的？

    生1：y=ax2+（b-1）x+c是二次函数，我需要找出a，b-1，c的正负情况.

    师：你有答案吗？

    生1：从二次函数y2=ax2+bx+c的图像我发现a>0，c>0，b-1的正负情况还没找到.

    生2：我的答案是选择A.

    师：这么快就得到了，你是怎么想的？

    生2：两个函数图像的交点坐标可以通过建立方程组y=x，y=ax2+bx+c求解，代入消元得x=ax2+bx+c. 因为P，Q两点在第一象限，所以方程x=ax2+bx+c有两个正实数根，即方程ax2+（b-1）x+c=0有两个正实数根，观察图像可知答案为A.

    实施意图? 函数与方程虽是两个不同的数学概念，但在解题中它们之间相互联系、相互渗透，一个函数若有解析式，那么这个解析式就可以看成是一个方程，它的两端可以分别看成函数，因此，许多有关方程的问题可用函数的方法解决;反之，许多有关函数的问题也可以用方程的方法解决.

    写在最后

    函数与方程思想在整个数学体系中有着基本而又重要的地位，它是中小学数学教学的核心内容，在中考复习中教师应予以重视. 教学中，教师应结合具体问题，运用函数方程思想构建数学模型，借助数形结合化抽象为具体，帮助学生准确地分析、快速地解答，加深学生对函数方程思想的理解，使学生能够学以致用，实现思想方法的内化，优化学习效果，提升学生的综合素质.