非惯性系中的牛顿运动定律
孙尔林

人们把参考系进行了分类,凡是牛顿第二定律能够适用的参考系称为惯性参考系,反之,牛顿第二定律不适用的参考系称为非惯性参考系.牛顿第二定律所谓是否适用,我们考虑的因素实际上是力的产生条件,如果具备力的产生条件,则必然符合牛顿第二定律.通过总结,人们发现,凡是相对地面静止或者做匀速直线运动的参考系都是惯性参考系,而相对于地面做变速运动的参考系是非惯性参考系;在众多的惯性参考系中,相对地面静止的惯性参考系具有特殊的优点,把它叫做绝对惯性参考系.
牛顿的力学规律只适用于惯性参考系,那么非惯性系中牛顿运动定律就不适用,为了建立形式与牛顿第二运定律一致的动力学方程,就需要引入惯性力的概念.下面从非惯性系的力学规律和规律的应用两个方面分析讨论.
一、非惯性系中的力学规律
设非惯性系参考系的加速度为a',物体相对于非惯性系的加速度为a,物体的实际加速度为a+a'.
根据牛顿第二定律
F合=m(a+')
F合-ma'=ma
令F惯=-ma',方向与a'的方向相反.很明显,“惯性力”大小取决于物体的加速度大小,而物体的加速度大小实际又取决于非惯性参考系相对于惯性参考系的加速度.惯性力是虚构的力,不是真实力,惯性力不是自然界中物体间的相互作用力,因此不属于牛顿第三定律涉及的范围之内,它没有施力物体,不存在与之对应的反作用力.
在非惯性系中,考虑到惯性力后的动力学方程为
F合+F惯=ma
二、非惯性系中的力学规律的应用
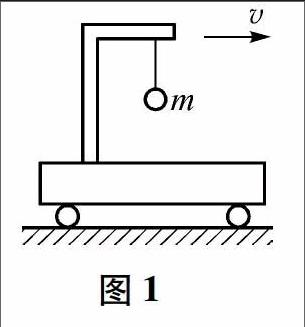
例1 如图1所示,小车的支架上通过细绳悬挂有质量为m的小球,当小车从静止开始以加速度a向右做匀加速运动时,小球将怎样运动?
解析 以小车作为参考系,小车做变速运动,小车从静止开始以加速度a向右做匀加速运动时(此时设向右为正),小球除了受到真实的力——重力G和绳子的拉力F外,还受到方向向左的惯性力F,因此小球向左偏离,当偏离竖直方向为某一角度θ时,F和G的合力与惯性力大小相等、方向相反,小球相对于车厢静止.
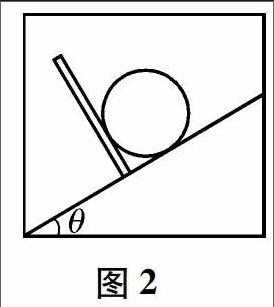
例2 一个质量为m的光滑小球,置于升降机内倾角为θ的斜面上,如图2所示.另一个垂直于斜面的挡板同小球接触,挡板和斜面对小球的弹力分别为N1和N2.起初,升降机静止,后来,升降机以a向上加速运动.
试求挡板和斜面对小球的弹力分别为多少?
解析本题中如果以升降机为参考系(非惯性参考系),则小球处于静止状态,即处于平衡状态.小球的受力情况如图3所示,则(其中,f为惯性力的大小):
N1sinθ+N2cosθ=mg+f
N1cosθ=N2sinθ
f=ma
解得
N1=m(g+a)sinθ
N2=m(g+a)cosθ
例3 一质量为m。,倾角为θ的斜面体放在水平面上,在斜面体上有一质量为m的物体.为使m不与斜面发生相对运动,现用一水平力F作用在mo上,如图4所示.
(1)若所有接触面均光滑,F应多大?
(2)若m与mo之间的动摩擦因数为μ,而mo与水平面间无摩擦,求F的范围.
解析在m不与斜面发生相对运动时,以地面为参考系,对m与mo整体应用牛顿第二定律有:
F=(m+mn)a
以mo为参考系(加速直线运动的非惯性系),沿斜面向下和垂直斜面向上为x、y的正方向,以m为研究对象,加上水平向左的惯性力ma后,对m应用牛顿第二定律:
x方向:mgsinθ+f-macosθ=0
y方向:N-mgcosθ-masinθ=0
m与mo不发生滑动的极值条件为:
f=±Nμ
联立可得:
所有接触面均光滑时,μ=0,此时,F=(mo+m)gtanθ.
例4 在一体积为V,质量为mo的铁盒内置有一阿特伍德机,已知两物体的质量分别为m1和m2.现将此铁盒放入密度为p的液体中,如图5所示,试求铁盒在下沉过程中的加速度.忽略液体对铁盒的阻力作用.
解析 如图5所示,以液体为参考系(惯性系),向下为正方向,设m1、m2之间的绳中张力为T
以mo为研究对象有:
mog+2T-pVg=moa
以铁盒为参考系(加速直线运动的非惯性系),设向下为正方向,分别以ml、m2为研究对象,分别加上-mla,-m2a的惯性力,m1、m2相对于铁盒具有等值的加速度a相应用牛顿第二定律:
对m1:m1g-T-m1a=m1a相
对m2:m2g-T-m2a=m2(-a相)
联立解得:
在非惯性系中分析问题,有独特的优势,可以简化分析问题的思路,优化解题步骤,但必须要正确处理惯性力,要抓住研究对象相对非惯性系的运动情况,在引入惯性力之后,正确列出动力学方程是关键.



人们把参考系进行了分类,凡是牛顿第二定律能够适用的参考系称为惯性参考系,反之,牛顿第二定律不适用的参考系称为非惯性参考系.牛顿第二定律所谓是否适用,我们考虑的因素实际上是力的产生条件,如果具备力的产生条件,则必然符合牛顿第二定律.通过总结,人们发现,凡是相对地面静止或者做匀速直线运动的参考系都是惯性参考系,而相对于地面做变速运动的参考系是非惯性参考系;在众多的惯性参考系中,相对地面静止的惯性参考系具有特殊的优点,把它叫做绝对惯性参考系.
牛顿的力学规律只适用于惯性参考系,那么非惯性系中牛顿运动定律就不适用,为了建立形式与牛顿第二运定律一致的动力学方程,就需要引入惯性力的概念.下面从非惯性系的力学规律和规律的应用两个方面分析讨论.
一、非惯性系中的力学规律
设非惯性系参考系的加速度为a',物体相对于非惯性系的加速度为a,物体的实际加速度为a+a'.
根据牛顿第二定律
F合=m(a+')
F合-ma'=ma
令F惯=-ma',方向与a'的方向相反.很明显,“惯性力”大小取决于物体的加速度大小,而物体的加速度大小实际又取决于非惯性参考系相对于惯性参考系的加速度.惯性力是虚构的力,不是真实力,惯性力不是自然界中物体间的相互作用力,因此不属于牛顿第三定律涉及的范围之内,它没有施力物体,不存在与之对应的反作用力.
在非惯性系中,考虑到惯性力后的动力学方程为
F合+F惯=ma
二、非惯性系中的力学规律的应用
例1 如图1所示,小车的支架上通过细绳悬挂有质量为m的小球,当小车从静止开始以加速度a向右做匀加速运动时,小球将怎样运动?
解析 以小车作为参考系,小车做变速运动,小车从静止开始以加速度a向右做匀加速运动时(此时设向右为正),小球除了受到真实的力——重力G和绳子的拉力F外,还受到方向向左的惯性力F,因此小球向左偏离,当偏离竖直方向为某一角度θ时,F和G的合力与惯性力大小相等、方向相反,小球相对于车厢静止.
例2 一个质量为m的光滑小球,置于升降机内倾角为θ的斜面上,如图2所示.另一个垂直于斜面的挡板同小球接触,挡板和斜面对小球的弹力分别为N1和N2.起初,升降机静止,后来,升降机以a向上加速运动.
试求挡板和斜面对小球的弹力分别为多少?
解析本题中如果以升降机为参考系(非惯性参考系),则小球处于静止状态,即处于平衡状态.小球的受力情况如图3所示,则(其中,f为惯性力的大小):
N1sinθ+N2cosθ=mg+f
N1cosθ=N2sinθ
f=ma
解得
N1=m(g+a)sinθ
N2=m(g+a)cosθ
例3 一质量为m。,倾角为θ的斜面体放在水平面上,在斜面体上有一质量为m的物体.为使m不与斜面发生相对运动,现用一水平力F作用在mo上,如图4所示.
(1)若所有接触面均光滑,F应多大?
(2)若m与mo之间的动摩擦因数为μ,而mo与水平面间无摩擦,求F的范围.
解析在m不与斜面发生相对运动时,以地面为参考系,对m与mo整体应用牛顿第二定律有:
F=(m+mn)a
以mo为参考系(加速直线运动的非惯性系),沿斜面向下和垂直斜面向上为x、y的正方向,以m为研究对象,加上水平向左的惯性力ma后,对m应用牛顿第二定律:
x方向:mgsinθ+f-macosθ=0
y方向:N-mgcosθ-masinθ=0
m与mo不发生滑动的极值条件为:
f=±Nμ
联立可得:
所有接触面均光滑时,μ=0,此时,F=(mo+m)gtanθ.
例4 在一体积为V,质量为mo的铁盒内置有一阿特伍德机,已知两物体的质量分别为m1和m2.现将此铁盒放入密度为p的液体中,如图5所示,试求铁盒在下沉过程中的加速度.忽略液体对铁盒的阻力作用.
解析 如图5所示,以液体为参考系(惯性系),向下为正方向,设m1、m2之间的绳中张力为T
以mo为研究对象有:
mog+2T-pVg=moa
以铁盒为参考系(加速直线运动的非惯性系),设向下为正方向,分别以ml、m2为研究对象,分别加上-mla,-m2a的惯性力,m1、m2相对于铁盒具有等值的加速度a相应用牛顿第二定律:
对m1:m1g-T-m1a=m1a相
对m2:m2g-T-m2a=m2(-a相)
联立解得:
在非惯性系中分析问题,有独特的优势,可以简化分析问题的思路,优化解题步骤,但必须要正确处理惯性力,要抓住研究对象相对非惯性系的运动情况,在引入惯性力之后,正确列出动力学方程是关键.

