数学对称美与统一美在中小学数学教学中的应用

    罗建华

    【摘要】如果我们能细细品味数学那些枯燥公式，烦琐证明之后的本质规律，就能体味到一种独特的美，那是数学所特有的美：逻辑上的严谨性、结构上的协调性、理论上的抽象性、应用上的广泛性以及其方法之优美与奇特、其形式之间的对称与和谐、其内容的丰富与深刻等等，无不给人以美的感受，美的刺激，美的热爱。美育，是培养人们认识、发现、体验、欣赏和创造美的能力的一种教育方法。我们可以通过美育促进受教育者获得美的理想、美的品质、美的修养和美的情感。一方面，中小学数学教育是为学生建立一个基本的逻辑体系，另一方面是为了学生做到主动学习，喜爱学习，最后形成终身学习的习惯，这才是中小学数学教育的立足点与支撑点。

    【关键词】对称美；统一美；數学教学

    曾经有教育家说过：“没有美和艺术的教育，在我看来是不可思议的。”进入21世纪的今天，审美教育这个新名词渐渐被人们所提起。音乐、体育、美术等艺术类科目首先想起号召，开展了大量的美育活动，紧接着语文、英语也做出了改变，唯独数学无动于衷、迟迟不动。这是为什么呢？难道是数学缺少美吗？古希腊的哲学家柏拉图就已经发现数学是一个巨大的美学宝库，例如对称美、统一美、比例美以及黄金分割等等。许多老师曾为学生不喜欢数学而苦恼，然而只要我们在教学中引导他们发现美，让课堂变得活跃起来，激发他们的兴趣，焕发他们的热情，再好好地培养他们的兴趣，何愁不能提高他们的成绩。由于本人才疏学浅，仅仅对数学的对称美和统一美有些浅薄的研究，希望对数学教学起到些作用。

    一、数学中的对称美

    数学知识中的对称有很多，但我们常见的只有三类：其一为轴对称，代表图形有等腰三角形、长方形；其二为中心对称，代表图形有平行四边形、正方形等；形式上的对称，比如加减乘除、正反比等。教师在课堂上可以渗透对称的思想，比如教室内常见的黑板、讲台都是对称的，具体来说是轴对称。

    在所有对称图形中，最令人惊叹是圆这个简单的曲线。它的对称轴有无数条，即便是作为一个中心对称图形，它也很特殊。一般的中心对称图形必须绕其对称中心旋转180度后才能跟原图形重合，而圆不一样，将它绕其中心旋转任意一个角度后都能跟跟原图形重合，这就是圆所独有的性质，让人不禁赞叹它是最完美的曲线图形。

    （一）创设美的情境，让学生感受数学的对称美

    在课堂上用课件放出美丽的轴对称图形，可比干巴巴地讲课生动、形象多了，并且通过多媒体的放映，可以创立一个美的情境，让学生置身于美中，全身心地感受到对称美，在美境中得到成长。比如在学习轴对称这一章时，教室可以这样说：“同学们，在这个世界上存在着许多轴对称图形，你们认为它是美的吗？当然是美的，正是因为有了这些美丽的轴对称图形，我们的世界才会变得如此五彩缤纷、丰富多彩！好了，就让我们走近轴对称图形，去解开她那神秘的面纱。”[动画呈现：有美丽迷人的泰姬陵、庄严肃穆的金字塔、雄伟壮丽的富士山和历史悠久的巴黎圣母院等名胜古迹；有圆、矩形、椭圆、等腰三角形、正五边形等各种图形；还有漂亮的小蜜蜂，可爱的青蛙，美丽的蝴蝶等各种小动物……]随着时间的推移，学生的情绪调动了起来，发出此起彼伏的赞叹声。学生已经完整地感受到了对称图形的美，师：“正因为有了这么多对称与不对称，才让我们的世界变得如此五彩缤纷、美丽动人。”通过这些美丽的画面，让学生欣赏到对称美，并产生追寻美的渴望。

    师：刚才老师展示了那么多的轴对称图形，想必同学们已经对轴对称图形有了深刻的认识，不知道你们能不能画出一幅老师最喜欢的轴对称图形？

    经过前面的铺垫，学生基本上理解了轴对称原理，现在进行创作不仅可以锻炼他们的动手能力，还可以进一步巩固加深对知识的理解，教师在下面巡查，也可以查漏补缺。

    本节课将要结束时，学生自主创作出来许多作品，如枫叶、彩虹、气球等等。在本节课的作品展示环节，通过学生自己向全班介绍作品，加深了学生对对称的理解，也表现了数学对称美的文化内涵。

    （二）探索美的秘密，创立美的等式

    探索、发现、创造三部曲不仅是人类求知过程，也是一种常用的教学手段，例如我们可以在先在黑板上写出一些对称等式，让学生仔细观察，再提出一个问题，其实答案就隐藏在等式之中，等到学生苦苦探索，最终得到规律答案，并利用规律创造新的等式。多媒体出示：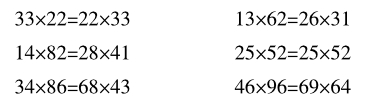

    师：请同学们仔细观察上面的6个等式，你觉得美吗？为什么？你能找出它的规律吗？

    前面两问比较容易，学生一下子就答出来了。可是对于最后一问，全班都陷入了沉默，见此情况教师决定给几分钟讨论。学生经过激烈的讨论最终发现了算式的秘密：1.每个算式都关于等号对称；2.两个个位、十位互换的两位数的乘积等于两个原两位数的乘积。

    师：刚刚我们得到了对称等式的特征，你们能不能根据它的规律创造出一些类似的算式？

    听到这话，学生们跃跃欲试，不一会儿就创造出很多对称等式，现出示一部分：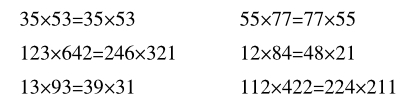

    数学美育的魅力在于让学生通过探索发现，不断发现对称美的秘密，并依据规律创造出对称美。这样不仅锻炼了学生发现美的能力，还激发了他们探索美的热情。

    从回文数中得到启发，巧解等差数列，回文数是指正序读、反着读都是一样的整数，例如：1001、343、78987等。在回文数的整数乘法中，我们发现了一个有趣的现象：1×1=1，11×11=121，111×123=12321。

    我们通过仔细观察发现出规律，并巧算出：111111111×111111111=12345678987654321，回文数在数学算式上的巧妙应用正是反映了对称美，从而引起学生浓厚的兴趣。

    （三）从轴对称图形中发现对称原理的运用

    在我们学习了轴对称图形后，最常见的习题就是画出轴对称图形的另一半。其实轴对称图形为人们研究数学问题提供了某些启示，例如在博弈论中也经常用到对称理论，有一道经典的题目：

    一张桌面上摆了一排糖果，共计41个，有两个小朋友比赛看谁能拿到最后的糖果就算赢，游戏规则是每人每次只可以拿一颗，最多拿两颗，但是拿两颗糖果时必须是相邻的，即中间没有其他的糖果，证明：先拿的人一定有办法使对方输。这题表面上看挺难的，以为从排列组合的角度来看，分法太多了，但是如果从对称的角度来看却十分容易。当先手拿走了最中间的那一颗（第二十一颗糖果）后，左、右两边都各剩二十颗糖果，只要对方拿一边的糖果，你就拿另一边的糖果，而且位置、个数都和对方对称，只要对方拿多少，你也拿多少，因为是对称的，所以最后一次肯定是你的，因此先拿的人肯定是赢家。如果糖果是40粒，即偶数个时，只要你第一次拿走了中间的两粒，使左、右两边各剩19颗糖果，就能保证必胜。

    解答的思维方法来源于轴对称图形的基本特征，教师在教授轴对称图形性质特征时，可以部分引用这方面的知识，加深对轴对称图形知识的运用和深层理解，使学生乐于学习，发现对称的美，领略到数学的魅力，激发学生发现美、鉴赏美、创造美的能力，并培养学生高尚的审美情趣。

    二、数学中的统一美

    在数学现象中，统一无处不在，图形中：长方形、正方形统称为矩形，因为它们的特征都是四个直角和两对互相平行的线段；正数和负数这两对冤家也可以统一到实数中去。

    （一）结论的统一美

    一个统一的结论可以揭示自然界的一些秘密，促进人类社会的发展进步，人类的发展史就是一个不断追求统一结论的过程。而作为所有学科的基础，人类发展的基石———数学更是如此，我们对数学现象的所有分析都形成了无数个统一的结论，然而这只是冰山一角，自然界中还有许多没有发现的结论等着我们。我们数学教材中的每一个公式，每一个定理都是一类问题的统一结论，也是最高度的概括与总结。例如，矩形的四个角是直角。除了公式和定理具有统一性外，许多看似毫无关系的问题也能得出统一的结论。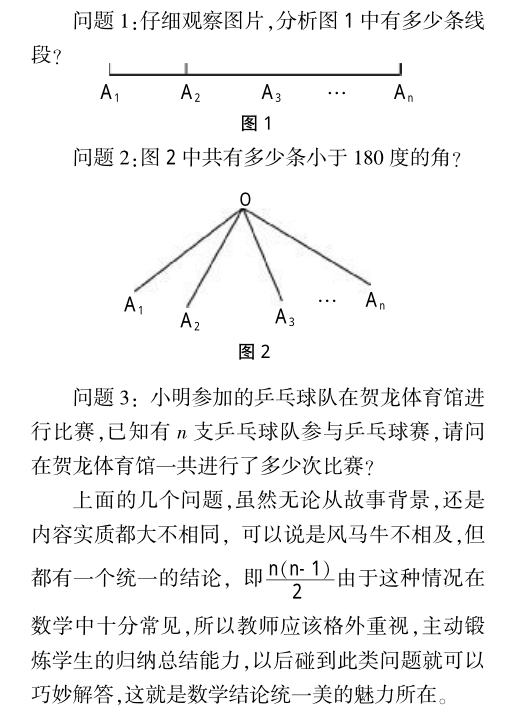

    （二）方法的统一美

    数学中有许多常见的方法，它们的应用十分广泛，如消元法、降次法、图像法、代入法等等，它们在数学解题中扮演着十分重要的角色。

    例如，二元一次方程可以用消元法或代入法解出未知数，一元一次方程组也可以用图像法得出答案。

    举个简单的例子，我们在计算五边形的内角和，可以轻易地想出以下几种方法：

    方法1：如图3，连接AD两点，再连接AC两点，我们可以看到线段AD、AC将五边形ABCDE分成三个三角形，因为一个三角形的内角和是180度，那么五边形的内角和为180×3=540度。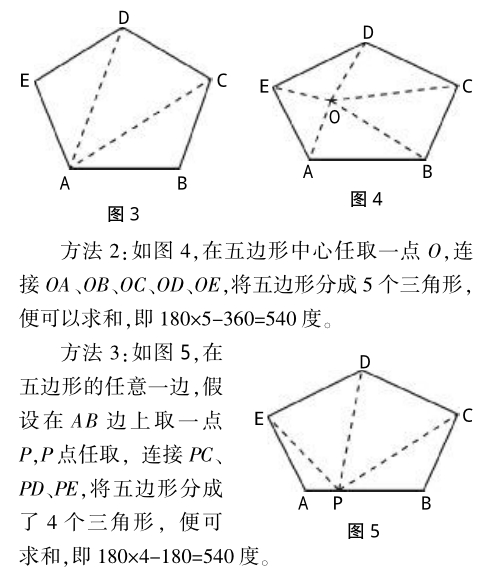

    我们一直观察发现，上述的三种解法，都有两点统一的特征：（1）都是每个顶点跟任意一点连接，这个点可以是顶点，也可以是五边形内部的一点，甚至可以是五边形一边上的任意一點；（2）将求五边形内角和的问题，转化成求几个三角形内角和相加的问题。看到这里，有同学不禁想到如果任意一点是在五边形的外面，那么还能构造出三角形来求五边形的内角和吗？其实是可以的，方法同上面三种解法一样，我就不详细论述了。对不同的解题方法进行概括总结，得出统一的结论，有助于学生深刻地理解问题本质，拓展思路，锻炼解题技巧，感受统一美的魅力。

    （三）过程的统一美

    我们在学习矩形、平行四边形等数学图形的过程都经历了定义、性质、认识、应用的四个环节，无独有偶，学习全等、相似等数学关系的时候也是经历了这四个环节。而我们在学习一元一次、二元一次等方程的过程都经历了概念、解法、应用的三个阶段。知识点的研究过程可以统一，那么数学的解题过程也有统一美吗？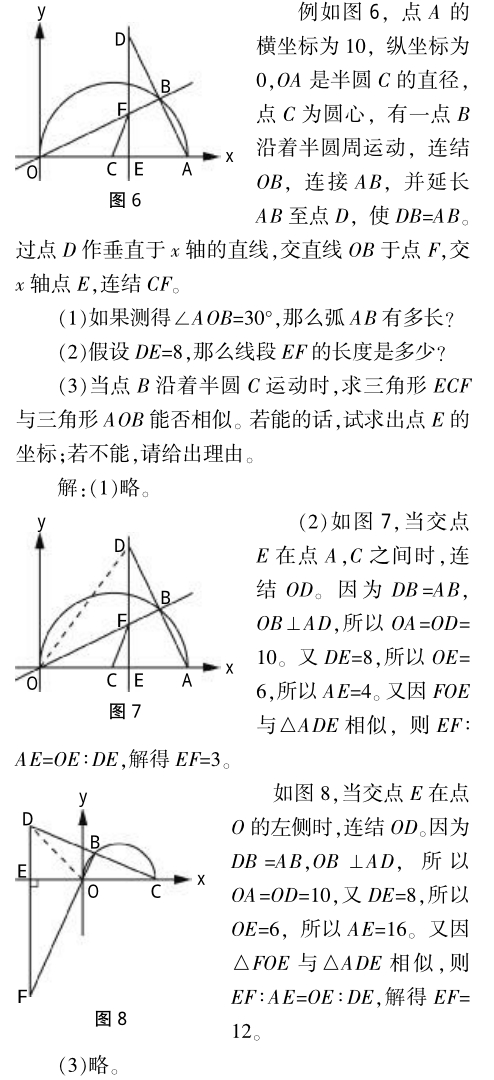

    注：我们发现在解答第二问的时候有两种情况，在这两种情况中的图形差异很大，得出的结论也不一样，但是解题过程却出乎意料的一致。这种解题过程的高度统一在第三问中也存在着，第三题共有六种情况，除了两种情况无解外，其他几种情况的解题过程基本一致，这里就不赘述了。

    从这道题中，我们可以发现图形通过平移、旋转等变换改变了位置和形状，但是解题的过程却是高度的统一，从这种统一上，学生可以得到思路的启发，找到快速简捷的解决问题途径，这就是统一美的意义所在。

    三、对未来数学教学模式的思考和建议

    渗透数学美在数学不仅是教学过程中体现的数学之美无处不在，也刺激了课堂气氛，吸引学生的学习兴趣，使学生形成微妙的一个美丽的培养。

    教材里潜藏的美学因素，教师应在课堂教学中揭示出来，让学生自然地认识到数学的美。教师可以引导学生获取新知识与审美特征。通过必要的实践中获得感悟，再发现新的知识与美学。学生通过这个过程培养了审美直觉能力，提高了实践创造能力。

    教师在课堂教学中要注重于引导学生的审美意识，适当地将数学中美的因素呈现出来，让学生体验到数学的美感。

    教师可以探索数学美的教科书，培养学生的感受美，欣赏美，让学生可以用美学方法在数学创造美的能力。

    因此，在教学实践中，学生可以更轻松，更快乐地学习数学知识，掌握数学技能，形成了学习气氛，是自觉的，轻松的，活泼的。

    【参考文献】

    [1]周欣.谈谈数学的美[D].南昌十八中，2006.

    [2]刘鹤翔.小学数学教学中美育渗透的问题及对策研究[D].哈尔滨师范大学，2017.

    [3]杨云.中心仿射曲面和余二维中心仿射浸入[D].东北大学，2010.

    [4]张水根.认真挖掘新教材中存在着的数学美[J].龙岩师专学报，1998.

    [5]韩诗贵.浅议初中数学教学的统一美[D].江苏省无锡市惠山区省锡中实验学校，2016.

    [6]郭育红，夏立华.高师应加强数学美教育[J].河西学院学报，2002.

    [7]蔡小真.浅析数学在素质教育中的美学价值[J].福建广播电视大学学报，2010.

    [8]陆灵俊.巧用情商因素优化数学教学[J].广西教育，2005.

    [9]杨云.三维Minkowski空间中二次曲面的分类[D].东北大学，2006.

    [10]荣伟.数学校本课程开发[D].内蒙古师范大学，2012.