溯洄从之，一波三折

    陈凯

    

    

    

    蒹葭苍苍，白露为霜。所谓伊人，在水一方。

    筆者何以突发雅兴，大家且看下面发生在实际教学中的需求。

    在人工智能的图像或声音识别任务中，常会遇见卷积运算的环节。所谓卷积运算，是将特定的卷积核与卷积区域进行点乘然后取和，从计算过程上看并不复杂，而不同卷积核对图像特征提取的效果，也可以很直观地展现出来，网络上很容易找到大量的卷积运算及特征提取的实际案例，也可以下载卷积运算的代码，手动更改卷积核，并观察特征提取的效果。

    例如，在GitHub上可以找到名为“python-conv2d”的代码，下载后就能轻松定制卷积核提取图像特征，图1和图2所展示的就是对图片进行边缘提取前后的画面，而图3则是用来进行边缘提取的卷积核。

    卷积核的点乘计算过程简单，相关资料很容易找到，本文不做展开，然而，教学中可能遇到的一个大问题，是解释“何以各种卷积核能达到特定的特征提取的效果”。这个问题并不容易回答，因为在解释过程中，必然要回溯到滤波器的概念，进而再回溯到与信号处理相关的若干数学概念。这便让笔者想起《蒹葭》中的诗句来：

    溯洄从之，道阻且长。溯游从之，宛在水中央。

    尽管道阻且长，但抱着不惧波折、追根究底的精神，尽可能亲自回溯源头，哪怕是远观佳人绰约风姿，总好过道听途说、人云亦云。本文将要介绍的几个小实验，或可成为溯源之舟。

    ● 简单的叠加，不简单的分离

    为了能够更简单地展现出特征提取的原理，就要先创造出尽可能简单的数据。相较于数据量庞大的图像和声音，可以试着创建一系列项目数有限又能展现出波的图样的数据，将数据放置在一维的存储空间中，利用数据的变化，来解释特征提取的意义与方法。这里使用电子表格这种简单且直观的工具，创建两个频率不同的正弦波，然后再将两个波进行叠加。

    ①使用拖拽功能，在电子表格的第一行生成一个差值为10的等差数列，数列项可以略多一些，如从0、10、20、3一直到720，此数据用以反映正弦波在横轴上角度的变化。

    ②使用公式“=A1*3.14159/180”，

    在第二行拖拽生成对应第一行角度值的弧度值。

    ③使用公式“=2*SIN（A2）”，在第三行拖拽生成正弦波Y=2*SIN（X）的函数的值，为叙述方便，称为正弦波A。以上过程的部分数据和波形图如图4、图5所示。

    ④使用与上面类似的方法，生成正弦波B的数据和图像，正弦波B的角度数据项差值为60，函数为Y=SIN（X），也就是说，生成的正弦波B的频率是正弦波A的6倍，振幅是正弦波A的一半。由于角度数值的差值比较大，所以这个正弦波看上去不太平滑，但不影响后续操作。部分数据和波形图如图6、图7所示。

    ⑤使用拖拽功能对两个正弦波相加，得到如图8所示的部分数据和如图9所示的波形，称为波C，当然，这不再是一个正弦波。

    接下来的任务，当然就是假装不知道波C是如何产生的，而要想办法对波C进行某种操作，使得波C中不同频率的波形（特征）能重新显现出来。可以发现，虽然两个波的叠加产生新的波形很容易，但若要将一个叠加而成的波分离开来，却麻烦多了。例如，为了让高频率的波形（即正弦波B）重新呈现出来，就要过滤掉低频率的波，反之亦然。可以很容易看出，所谓特征提取，其实与滤波有关。因篇幅有限，本文只围绕高频信号的提取，讨论相关教学策略。

    ● 简单的假设，不简单的过程

    想一想，为了实现高频信号提取的任务，可以采用哪些方法？教学中，不妨鼓励学习者展开一番头脑风暴。

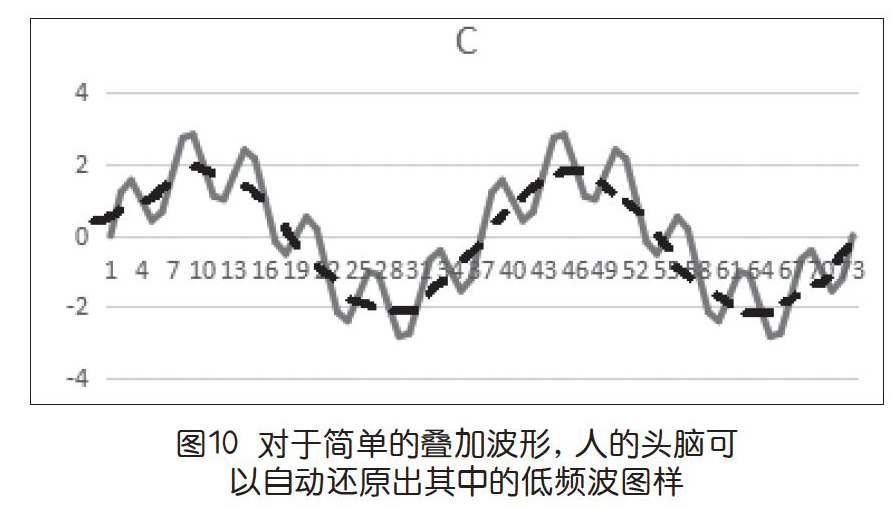
    一个容易想到的解决思路是：既然当前波C是两个波的叠加，那么，只要将当前的波C减去一个低频的平滑的波形，就可以获得高频的波B的图样了。从直观上看，这个低频的波的形态大致如下页图10中的虚线所示。

    虽说大家心知肚明，这个低频波的图样应当和Y=2*SIN（X）函数图像有关，但这里却只能继续玩假装不知道的游戏，因为要设法让计算机自己找到能契合图样的数据，而计算机当前可以利用的，就只有波C的数据。

    开展头脑风暴所获得的解决方案可能有：对邻近连续的几个数据取平均值，或许能获得一个低频的平滑的波X;不停地执行将“波峰”削除、“波谷”填满的操作，或许能获得一个低频的平滑的波X;找出当前波的局部最大值和局部最小值，取局部最大值和局部最小值的平均值，利用这些平均值或许可以描画出一个低频的平滑的波X……然后，将波C减去这个新生成的低频的波X，观察能否提取出高频的信号。

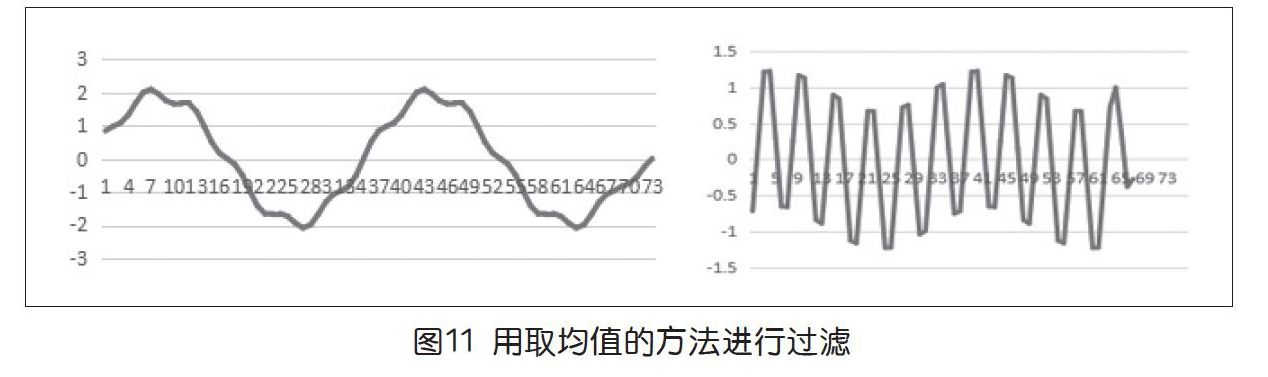
    第一个方案实现起来比较简单，但较难获得平滑的低频波形。下页图11分别是通过用邻近5个数据取平均值获得的低频波，以及用波形数据相减提取出来的高频波，提取后，高频的波形形态较好，但仍然有一定量的低频信号混杂其中（宏观起伏仍较明显），总体效果尚可。

    第二个方案中，为了削峰填谷，对每三个数据，取左侧和右侧的数据计算平均值，对获得的新的数据再反复进行迭代操作获得低频波。图12是进行四次削峰填谷的迭代操作后，获得的低频波和提取出来的高频波。效果看上去不错。

    第三个方案中，可以在电子表格中使用IF函数，通过比较大小获得局部最大值和局部最小值，然而麻烦之处是，每两个局部最大，或者每两个局部最小的数据，它们中间的数据应该如何填充？如果按电子表格中容易实现的方法，按邻近的局部最大值或局部最小值填充进去，获得的波就不可能是平滑的。操作结果如图13所示，特征提取的效果十分勉强。

    若是要改进方案三，使得低频信号变平滑，就要借助如插值、函数拟合之类的方法。在电子表格中实现是比较麻烦的。

    在教学中，为了培养学习者自主思考和探索的精神，教师应鼓励学习者大胆给出可能的解决方案，并尽力尝试用当前已有的工具，验证在具体的解答过程中，哪些方案更具有可行性，而不是直接将解决方案抛给学习者。

    ● 简单的表象，不简单的幕后

    在学习者充分思考了各种假设，并加以实施验证之后，教师最后抛出更优的方案，才更能促人思考。前文中提到可用取均值的方法来获得低频平滑的波，但正如图11所示，生成的低频波的图样一波三折，不是特别理想。不过，虽有不尽如人意之处，却能成为进一步研究的线索。

    之所以采用取均值的方法难以使波形平滑，从直观上看，是因为局部的波峰波谷过于突出，若是在取均值时，能降低突出部分的权重，加强非突出部分的权重，或许能使生成的低频波形的平滑度有所提高。

    例如，对于波形中的5个数据，按“=A1*0.25+B1*0.2+C1*0.1+D1*

    0.2+E1*0.25”公式获得C2表格中的数据（如下表）。

    若当前采样点处于局部波峰或局部波谷处，则公式的作用显而易见。但如果当前采样点不巧正在局部波峰和局部波谷的中间处，会不会反而将波峰和波谷处数据放大？对照波形图样计算一下就会知道，由于高频信号的周期性变化，按每5个数据取值，就算波峰和波谷数据同时被放大，在相加后，波峰处被放大的数据也会和波谷处被放大的数据相抵消。

    于是，可以用拖拽的方法，每5个数据生成一个加权平均值，并按生成的一系列加权平均值生成波形，该波形图样看上去相当平滑了（如上页图14）。用此波形，对波C做减法后，得到的高频波的图样也相当不错（如图15）。

    到了这一步，大家有没有想到，既然可以用取加权平均的方法获得低频的波形，那么，能否用同样的方法，直接把高频的波形提取出来？试一下就知道果然可以。例如，设“=A1*（-1）+B1*2+C1*（-1）”這样的公式，其思路是，将当前位置的数据权重加强，同时将当前位置两侧的数据权重减少。虽然说方法十分简单，但实施效果之出众，简直令人叹为观止。部分数据及波形图如图16所示。

    仔细观察就会发现，这个所谓的加权平均法，其实就是如假包换的卷积运算。这样一来，就只剩下一个问题：加权平均法中的“权”的取值，究竟应该怎么取才最为合理？这个地方，就立下了一个未来通往“傅里叶解析”这门课程的路标了。但对于大部分基础教育阶段的学习者来说，在人工智能的学习中，他们能够看到路标的存在并理解路标指向路径的意义，就算是完成学习任务了。在实际的特征提取任务中，通过反复试错，或者团队暴力搜索，再加上一点推理和空间想象力，要为加权平均法找出一套合理的权重值，并不困难，在课堂上，完全可以利用充足的人力，开展一项寻找合理权重值的挑战游戏。