排序问题

    

    

    

    算法园地

    编者按：教育部颁布的《普通高中信息技术课程标准（2017年版）》在“必修模块1的教学”中用专门的单元来谈论了算法，这说明，新课程要求高中信息技术在教学中应当以算法为要旨，强化算法的重要性。

    因此，本刊开设“算法园地”专栏，特邀北京大学计算机系原系主任李晓明教授、南京大学计算机系原系主任陈道蓄教授撰写有关算法的文章，为读者提供一些既有思想性又有实用性的材料。

    专栏的读者定位是对算法问题有兴趣的中小学教师，内容的铺陈将努力做到通俗性、趣味性和严谨性相结合。每月介绍一个算法，每期独立成篇，大体按照以下六个方面展开：应用背景、算法描述、实例模拟、性质分析、思考问题、参考代码。你以前如果学过算法，在这里会看到一种不同的视野;你以前如果没有学过算法，则可以通过对每月一个算法的学习，既领悟到算法思想的精髓，又形成算法实战的能力。

    我们已经知道，在排好序的文档中搜索，效率会比在没有排好序的文档中高得多。任何数据处理系统中可能都会用到排序算法，且可能使用频繁，因此排序的效率尤为重要。

    排序一般是根据输入数据对象的关键字进行。关键字均取自某全序集，全序集是指其中任意两个元素均可“比大小”的集合。排序算法将输入元素按照定义的次序要求输出。为了简单，我们假设输入元素均为正整数（对象即关键字），编程时可以采用一维数组或List结构，且序列中不含相同元素，任意两个元素比较一定有大小之分。输出为严格递增序列。

    如果关键字的值是不可分解的，算法能够执行的基本操作只是比较两个关键字的大小，这样的排序算法称为“基于关键字比较的算法”，本文主要讨论此类算法。（Python等语言库函数提供了针对List结构的排序功能，可以直接调用。当然这不在本文考虑范围内）

    ● “冒泡”排序算法

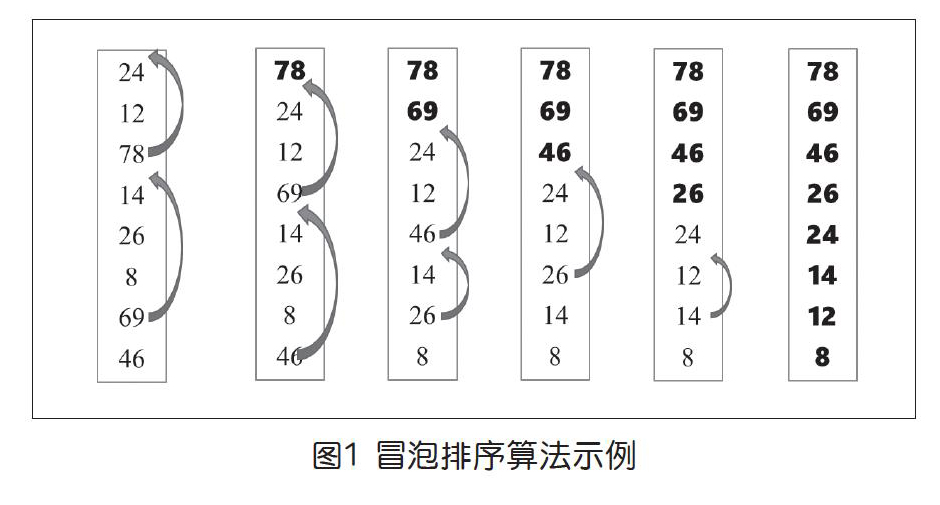
    对海量数据排序这是一个很大的挑战，不过，一些广为人知的计算机排序算法与人的思维方式并没有什么差别。很多程序设计初学者编写的第一个排序程序是“冒泡”排序，其基本思想可以用图1表示。

    图1中最左边的是输入序列（从下向上）。我们总是试图找出当前待处理区域中的最大元素，将它放到最高位置，这就像水中的气泡往上冒一样，所以称为“冒泡”排序。开始时待处理区域是整个序列，我们从最下面的位置开始依次向上做比较操作，一旦发现“逆序”，即上下位置与元素大小相反，则做一次“互换”。图1中的箭头表示连续执行“互换”的结果，已经放置到正确位置的元素用粗黑体表示，新一轮操作中这些位置不再包含在待处理区域中，重复执行上述过程，直到待处理区域只含一个元素为止。整个过程描述如下页图2所示。

    循环未必需要执行到k=0才停止，如果某一轮中swap一次也没执行，算法就可以停止了，这只需用一个标记变量即可。

    前面提到，排序过程中用“互换”操作消除“逆序”，一般意义上的“逆序”，是指两个对象位置下标大小与值的大小正好相反（也称它们的位序与值序不一致）。排序过程可以理解为消除输入序列中的所有“逆序”的过程，如果输入的数据值是严格递减的，那么任何两个元素均构成“逆序”，逆序的数量为O（n2）。“冒泡”排序算法总是比较相邻的两个对象，也只可能将两个相邻的对象互换，这意味着每次比较最多消除输入中的一个逆序，因此，最坏情况下算法执行的比较次数为O（n2）。根据随机输入使得任一处理区域中最大元素出現在任一位置的概率相等，很容易推知平均比较次数仍是平方数量级的。

    理论分析告诉我们，基于关键字比较的排序算法比较次数不可能比O（nlogn）更好，换句话说，如果算法的效率能达到O（nlogn），就是最优了。冒泡算法与最优的差距有多大呢？粗略地说，如果在特定计算环境下对100万的数据排序，某个O（nlogn）的算法需要1秒钟，O（n2）的算法可能需要10小时以上。

    ● 快速排序算法

    快速排序可能是应用最广的排序算法，其基本思想是将输入分解为两个规模较小的子问题，递归求解。算法首先调用函数partition，以一个任选的元素为“标杆”，将比标杆小的元素放入子集small，大的元素放入子集large。partition返回值是针对这样的分割，标杆元素应该处于的位置splitPoint。函数partition的结果如图3所示，快速排序过程如图4所示。

    接下来讨论如何实现partition。选第一个元素做标杆是随意的，因为输入的随机性，选任意元素效果是一样的。给定标杆，通过比较大小分出两个子集似乎很容易，但我们希望在“原地”操作，也就是说不用额外的存储空间（除了标杆本身），这需要一点“技巧”。我们用矩形框表示当前的待处理范围，调用partition时标杆已选定移出，因此第一个位置是空位。在partition执行期间始终保留一个空位。执行过程包含一个扩充small的过程与一个扩充large的过程，从large开始交替进行，同时空位也交替地出现在左或右（如上页图5）。

    每一次扩充过程的终止条件为：发现应该移动的元素或者遇到空位，如果是后者，则整个partition执行完成。图6所示为扩大子集small的过程，扩大子集large的过程与extandSmall是对称的，读者可自行完成。

    实现子问题分割的函数partition利用循环，交替地调用上述两个函数（如图7）。图8是一个例子执行过程的部分演示。

    快速排序避免了冒泡排序中只比较相邻元素的局限，那么其效率如何呢？递归算法的效率与需要递归的次数密切相关。一般而言，子问题规模下降快的话就会更快遇到终止条件，使递归次数下降。

    设想输入序列中数据严格递增，从人的观点看根本不需要计算，直接输出就是了。但是算法看不出这一点，选中的标杆恰好是最小元素，于是两个子问题一个是空序列，另一个规模比原输入只少一个元素。在这种原始输入数据条件下，很不幸的是每次递归都遇到同样情况。每次递归划分子问题执行比较操作次数为O（n），因此最坏情况下快速排序的代价仍然是O（n2）。

    其实这种极端情况出现的概率太小了，實际经验与概率推导都表明，在应用中快速排序完全可以降低O（nlogn）的时间复杂度，而且快速排序算法几乎不需要额外存储空间，其他额外开销也很小，所以应用广泛。

    前面提到过任一元素做标杆碰到最坏情况的概率是一样的（尽管各自的最坏输入不一样），但我们有个简单办法可以使碰到“最坏”输入的概率大大降低：随机从输入序列中选三个元素，用大小居中的元素做标杆。注意，不管如何选，调用partition时总让空位在首位。

    ● 合并排序算法：均衡分解子问题

    快速排序最坏情况下的表现不佳是因为两个子问题可能大小悬殊，如果我们采用递归方法时设法使两个子问题大小几乎相等是否会产生更好的算法呢？

    最简单地实现均衡分解的做法就是一切两半。为了简单，假设输入序列长度为2的整次幂，即n=2k经过k=logn轮分解，子问题规模为1，递归终止。将两个已经排好序的序列合成一个，过程如上页图9所示，合并排序过程非常简单（如上页图10）。

    显然，合并过程中每比较一次至少有一个元素进入合并区，所以合并的总比较次数不会超过合并区的大小。合并总共进行k=logn轮，每轮合并区的总规模为n，分解每个子问题的代价显然是常量，所以合并排序最坏情况的时间复杂度为O（nlogn），当然平均复杂度也不会更高。这意味着合并排序达到最优，但合并排序的应用远不如快速排序。对比前面讨论快速排序时讲到的一个优点，合并排序有个明显的缺点：合并不能在“原地”进行，需要O（n）的额外存储空间。

    ● 结束语

    并非所有的排序算法都是基于关键字比较的算法，有时候输入可能满足一些特别的条件，如输入对象的关键字是十进制表示的自然数，关键字可以分解为“位”。比较未必非得对整个数值进行，也可以逐位比较，还有些应用中我们可以预先知道关键字值的上下界。这些条件可以利用来设计出线性代价的排序算法。

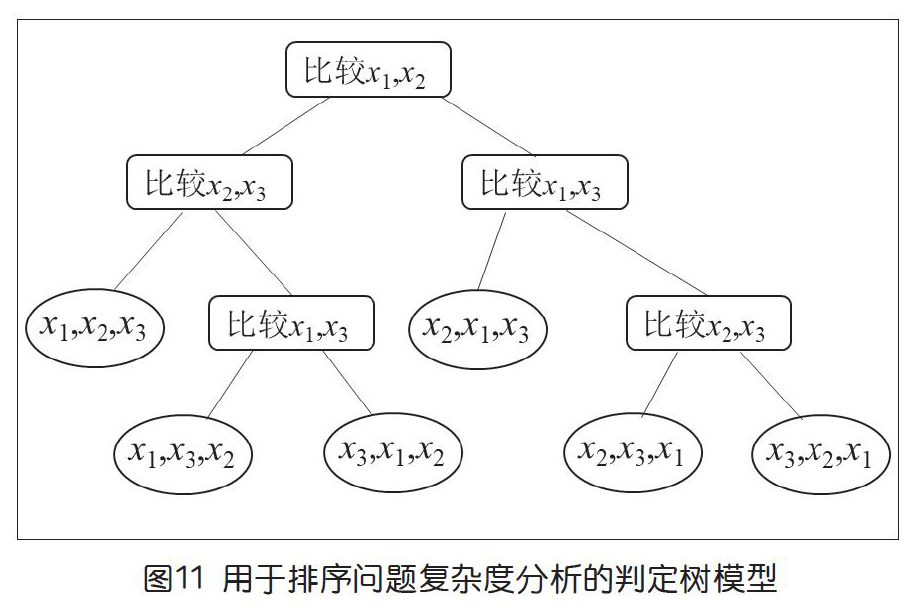
    有些读者可能非常好奇：即便限于关键字比较算法，以后完全有可能出现更聪明的人，想出更聪明的方法，现在怎么能确信不可能比O（nlogn）更好了呢？确实，对大多数问题判定算法的“最优”往往很困难，但对基于关键字比较的排序问题我们可用图11帮大家理解确定问题复杂度下限的基本思想。

    这里的下标1、2、3并没有任何特殊意义，所以这个图适用于一切对长度为3的序列排序过程。图11中中间节点（矩形）表示一次比较操作。在输入对象均不相等的假设下这是完全二叉树，左右两个子节点分别对应于“<”和“>”两种结果，而叶节点（椭圆）对应一种特定的排列，也就是排序问题的解。对任一输入，从根节点开始对关键字进行比较，并根据比较结果决定下一个操作。如果遇到叶节点，则算法终止，输出相应结果，图11中叶节点显示对象递增的次序。由于输入是随机的，解可能是输入序列的任意一种（重新）排列，而n个元素的序列可能的排列方式有n！个，所以对长度为n的输入，类似的算法树至少有n！个叶。而算法最坏情况下复杂度的下限是图11中从根到叶的最长路径的下界，当整个树是完全平衡树时这个下界最小，为log（n！），而log（n！）∈Ω（nlogn）。