“相互作用”中的特殊问题求解
房亚晶


特殊值法:这种方法与数学中的特殊值法有相似,但略有不同,数学中一般0或1为特殊值,而在高中物理学习中,我们会发现特殊状态(或位置)相当于数学中的特殊值.这些特殊状态(或位置),需要我们根据题目,联系所学知识,细细分析.
例1 如图l所示,一个空心均匀球壳里面注满水,球的正下方有一个小孔,在水由小孔慢慢流出的过程中,空心球壳和水的共同重心将会()
A.一直下降
B.一直上升
C.先升高后降低
D.先降低后升高
解析 初学者会认为空心球壳和水的共同重心在一直下降,忽略了水全部从空心均匀球壳流出时的这一特殊状态,此时空心球壳和水的共同重心变成了空心均匀球壳的重心,应为球心,与一开始装满水时一样.所以此题应选D.
特殊值法,不可简单地认为是题中的初状态和末状态这两个特殊状态,有时在过程中的某一状态也会为特殊状态,需要我们用心领会题意,细化过程,结合已学知识,才能很快地找出特殊状态解决问题.
假设法:就是假设某一条件成立,根据题意和已学的知识推导出结论,并检查这些结论是否符合题意,如果符合题意,即假设正确,如果不符合,即假设错误.
例2 画出图2中物体A和B所受重力、弹力的示意图.(各接触面均光滑,各物体均静止)
解析 物体A和B所受重力、弹力的示意图如图3所示.
图3中最右一幅图最易出错,我们可以借助于假设法来处理A球的受力情况,假设没有倾斜的墙面,能够保持原状,说明倾斜的墙面对小球没有压力的作用,小球只受到重力和地面对小球的支持力作用.
在判断静摩擦力的有无时,经常用到假设法.
例3 有三个相同的物体叠放在一起,置于粗糙水平地面上,物体之间不光滑,如图4所示.现用一水平力F作用在乙物体上,物体之间仍保持静止,下列说法正确的是()
A.丙受到地面的摩擦力大小为F,方向水平向左
B.甲受到水平向右的摩擦力作用
C.乙对丙的摩擦力大小为F,方向水平向右
D.丙对乙的摩擦力大小为F,方向水平向右
解析 假设甲物体不受乙物体对甲的静摩擦力,能静止于乙物体上,合力为零,所以甲物体不受摩擦力作用;对于乙、丙物体受到的静摩擦力大小和方向,可用整体法和平衡法相结合判断出静摩擦力的大小是F,答案为AC.
反推法:当我们不确定某一物理量时,我们可以利用其它物理量来反推出这一物理量.
例4 水平横梁一端A插在墙壁内,另一端装有一小滑轮B,一轻绳的一端C固定于墙壁上,另一端跨过滑轮后悬挂一质量为m=10kg的重物,∠CBA=30°,如图5所示,则滑轮受到绳子的作用力的大小为(g取10N/kg)()
A.50N
B. 20N
C.100N
D.
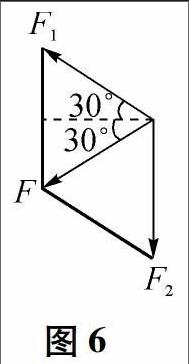
解析 滑轮受到绳子的作用力大小和方向不确定时,可根据三力平衡,反推出大小等效为两段绳中拉力F1和F2的合力,因同一根绳张力处处相等,都等于物体的重力,即F1=F2=G=mg=100N.可考虑应用平行四边形定则或三角形定则合成,如图6,本题选C.
总之,特别的问题采用特殊的方法、技巧内容处理,收到事半功倍的效果.特殊的方法很多,这需要我们不断积累,总结经验,才能运用得如鱼得水,并能够激发学习物理的兴趣.
(上接第18页)
解析 重心是重力的作用点,是一个物体受重力的总效果的反映.可根据重力的方向是竖直向下和二力平衡的条件来突破此题.如图4,先在A点把薄板悬挂起来,对于静止的薄板而言,只受重力和绳子上的拉力,由于这两个力必等大反向共线,即重力与绳子处于一条直线上,因此绳子的直线通过重心(重力作用点),即薄板的重心一定在AB直线上.然后在C点把薄板再悬挂一次,同理可知,薄板的重心一定在通过C点的竖直线CD上,AB、CD的交点在O,就是薄板的中心位置.
三、支撑法
只适用于细棒(不一定均匀).如图5,用一个支点支撑物体,不断变化位置,越稳定的位置,越接近重心.
一种可能的变通方式是用两个支点支撑,然后施加较小的力使两个支点靠近,因为离重心近的支点摩擦力会大,所以物体会随之移动,使另一个支点更接近重心,如此可以找到重心的近似位置.
四、针顶法
同样只适用于薄板.用一根细针顶住板子的下面,当板子能够保持平衡,那么针顶的位置接近重心.与支撑法同理,可用3根细针互相接近的方法,找到重心位置的范围,不过这就没有支撑法的变通方式那样方便了.
五、铅垂线法(任意一图形,质地均匀)
用绳子找其一端点悬挂,后用铅垂线挂在此端点上(描下来).而后用同样的方法作另一条线.两线交点即其重心.
六、理论计算法
物体的重心,可以依据杠杆平衡原理和支撑法原理,平衡时支点处即为重心位置,



特殊值法:这种方法与数学中的特殊值法有相似,但略有不同,数学中一般0或1为特殊值,而在高中物理学习中,我们会发现特殊状态(或位置)相当于数学中的特殊值.这些特殊状态(或位置),需要我们根据题目,联系所学知识,细细分析.
例1 如图l所示,一个空心均匀球壳里面注满水,球的正下方有一个小孔,在水由小孔慢慢流出的过程中,空心球壳和水的共同重心将会()
A.一直下降
B.一直上升
C.先升高后降低
D.先降低后升高
解析 初学者会认为空心球壳和水的共同重心在一直下降,忽略了水全部从空心均匀球壳流出时的这一特殊状态,此时空心球壳和水的共同重心变成了空心均匀球壳的重心,应为球心,与一开始装满水时一样.所以此题应选D.
特殊值法,不可简单地认为是题中的初状态和末状态这两个特殊状态,有时在过程中的某一状态也会为特殊状态,需要我们用心领会题意,细化过程,结合已学知识,才能很快地找出特殊状态解决问题.
假设法:就是假设某一条件成立,根据题意和已学的知识推导出结论,并检查这些结论是否符合题意,如果符合题意,即假设正确,如果不符合,即假设错误.
例2 画出图2中物体A和B所受重力、弹力的示意图.(各接触面均光滑,各物体均静止)
解析 物体A和B所受重力、弹力的示意图如图3所示.
图3中最右一幅图最易出错,我们可以借助于假设法来处理A球的受力情况,假设没有倾斜的墙面,能够保持原状,说明倾斜的墙面对小球没有压力的作用,小球只受到重力和地面对小球的支持力作用.
在判断静摩擦力的有无时,经常用到假设法.
例3 有三个相同的物体叠放在一起,置于粗糙水平地面上,物体之间不光滑,如图4所示.现用一水平力F作用在乙物体上,物体之间仍保持静止,下列说法正确的是()
A.丙受到地面的摩擦力大小为F,方向水平向左
B.甲受到水平向右的摩擦力作用
C.乙对丙的摩擦力大小为F,方向水平向右
D.丙对乙的摩擦力大小为F,方向水平向右
解析 假设甲物体不受乙物体对甲的静摩擦力,能静止于乙物体上,合力为零,所以甲物体不受摩擦力作用;对于乙、丙物体受到的静摩擦力大小和方向,可用整体法和平衡法相结合判断出静摩擦力的大小是F,答案为AC.
反推法:当我们不确定某一物理量时,我们可以利用其它物理量来反推出这一物理量.
例4 水平横梁一端A插在墙壁内,另一端装有一小滑轮B,一轻绳的一端C固定于墙壁上,另一端跨过滑轮后悬挂一质量为m=10kg的重物,∠CBA=30°,如图5所示,则滑轮受到绳子的作用力的大小为(g取10N/kg)()
A.50N
B. 20N
C.100N
D.
解析 滑轮受到绳子的作用力大小和方向不确定时,可根据三力平衡,反推出大小等效为两段绳中拉力F1和F2的合力,因同一根绳张力处处相等,都等于物体的重力,即F1=F2=G=mg=100N.可考虑应用平行四边形定则或三角形定则合成,如图6,本题选C.
总之,特别的问题采用特殊的方法、技巧内容处理,收到事半功倍的效果.特殊的方法很多,这需要我们不断积累,总结经验,才能运用得如鱼得水,并能够激发学习物理的兴趣.
(上接第18页)
解析 重心是重力的作用点,是一个物体受重力的总效果的反映.可根据重力的方向是竖直向下和二力平衡的条件来突破此题.如图4,先在A点把薄板悬挂起来,对于静止的薄板而言,只受重力和绳子上的拉力,由于这两个力必等大反向共线,即重力与绳子处于一条直线上,因此绳子的直线通过重心(重力作用点),即薄板的重心一定在AB直线上.然后在C点把薄板再悬挂一次,同理可知,薄板的重心一定在通过C点的竖直线CD上,AB、CD的交点在O,就是薄板的中心位置.
三、支撑法
只适用于细棒(不一定均匀).如图5,用一个支点支撑物体,不断变化位置,越稳定的位置,越接近重心.
一种可能的变通方式是用两个支点支撑,然后施加较小的力使两个支点靠近,因为离重心近的支点摩擦力会大,所以物体会随之移动,使另一个支点更接近重心,如此可以找到重心的近似位置.
四、针顶法
同样只适用于薄板.用一根细针顶住板子的下面,当板子能够保持平衡,那么针顶的位置接近重心.与支撑法同理,可用3根细针互相接近的方法,找到重心位置的范围,不过这就没有支撑法的变通方式那样方便了.
五、铅垂线法(任意一图形,质地均匀)
用绳子找其一端点悬挂,后用铅垂线挂在此端点上(描下来).而后用同样的方法作另一条线.两线交点即其重心.
六、理论计算法
物体的重心,可以依据杠杆平衡原理和支撑法原理,平衡时支点处即为重心位置,

