动态想象，让图形在头脑中生长

    阮传忠

    

    

    

    摘要：

    培养和发展学生的“空间观念”，是小学数学“图形与几何”领域的核心目标和内容。空间观念的培养主要依赖于学生的观察与操作，然而学生在面对较为复杂的“图形与几何”问题时，往往思维混乱，“眼中有物，脑中无形”，导致空间想象过程不能顺利进行，空间观念很难向纵深发展。本文从“图形与几何”的概念、特征、联系三个方面的教学现状入手，探寻实际教学中如何有效激发学生的“动态想象”，发展学生的空间观念。

    关键词：空间观念动态想象

    培养和发展学生的“空间观念”，是小学数学“图形与几何”领域的核心目标和内容，也是学生适应高层次学习和发展所必备的关键能力。然而，在实际教学过程中，我们的学生在面对较为复杂的“图形与几何”问题时，往往思维单一，缺乏对问题本质的深刻理解和全面把握，“眼中有物，脑中无形”，导致空间想象、推理过程不能顺利进行，数学思维很难向纵深发展。究其原因，主要是在教学时，老师习惯于让学生在大量的动手操作中直接获取表象，过分依赖于学生的观察与操作，忽略了学生必要的想象和推理过程。《数学课程标准》指出，在“图形与几何”教学中，应注重学生在观察、操作、想象、推理等学习活动中，发展学生的空间观念。所以，笔者结合“图形与几何”教学实践，谈谈如何从动手转向动脑，进而实现“脑手并用”，促使学生从单一的静态表象展开丰富的动态想象，让图形在头脑中生长，发展学生的空间观念。

    一、建构图形概念时进行动态想象

    在图形与几何的教学中，教师往往将目光聚焦在单个课时的图形概念上，忽视单元或学段知识之间的内在整体性联系;关注更多的是静止状态下的数学知识，忽视了基本图形之间的动态转化;过于关注图形表象特征的全面掌握，忽视对图形结构本质属性的把握。因此，在建构图形概念时，教师要适时启发学生在头脑中展开积极的动态想象，在动态想象中激活儿童思维的“沸点”，让其经历图形的运动、变化与生成，进而感悟基本图形之间的内在联系，从而帮助学生有效把握基本图形概念的本质属性。

    例如，在教学“长方体和正方体的认识”时，先对“一条线段经由垂直方向作平移，形成一个长方形，进而再将这个长方形沿与所在平面相垂直的方向平移，即可获得一个长方体”展开有效的“动态想象”，感悟到空间形体可被看成是由较简单的图形经由运动变化生成的思想。在学生初步认识长方体特征之后，通过相交于一个顶点的三条棱，让学生在头脑中还原出这个长方体的表象。这正是从思维的逆向角度对学生所学知识的有效重构。与此同时，教学中教师还不忘让学生说出还原过程中各个面与对应棱之间的关系，从而进一步加深学生对长方体面、棱、体三者之间关系的深刻理解，使其在边画边说的过程中，手脑并用，强化认知基础，抓住长方体和正方体结构特征的本质属性。通过这样的动态想象，学生眼中不仅有“物”，脑中更加有“形”，经历的是想象，留下的是思想。

    二、突破知觉障碍时进行动态想象

    我们知道，“图形与几何”领域有很多知识内容的教学，是需要借助于学生的直观操作去加以验证的。但有时这种“靜态”操作反而给学生的认知带来障碍，不利于学生对知识的正确理解。例如，在教学“三角形三边关系”时，对于其中“两边之和等于第三边”的情况，学生在动手操作后，常常会产生视觉错觉，认为也能围成一个三角形。究其原因，主要是直观的学具本身有宽度，再加上学生心里想围成一个三角形，所以在操作中左边挪一点、右边挪一点，再将上面两根小棒慢慢往下压，最后两根小棒的端点碰在了一起。仅从视觉上判断，很难让学生不相信围不成一个三角形。尽管有的老师对实验材料和方法进行了有效的改进，并大大减少了操作的误差，但还是很难让人信服。因此，如何突破“静态”操作中的视觉误差所产生的知觉障碍，就需要适时地展开“动态想象”。将头脑中已有的“两边之和等于第三边”的重合表象，在语言的描述下进行旋转变形——两条短边在上拱的过程中缺口会越来越大，激活学生的数理逻辑经验，想象出运动变化的过程和结果，从而在头脑中完成思维实验，突破教学难点，促进学生空间观念向纵深发展。

    “三角形三边关系”教学片断：

    课件演示（如图1）：6厘米和4厘米两根小棒正好和10厘米的小棒重合在一起。

    图1

    师：这是三角形吗？

    生：（齐）不是。三根小棒重合在一起，是一条线，而且中间没有空隙，需要将两根短棒的交点（公共顶点）往上拉。

    师：想象一下，如果固定两根短棒的一端，使其往上慢慢移动，这时它们的公共端点会发生怎样的变化？

    生：中间会分开，向左右两边慢慢打开。

    师根据学生的描述相机动态演示（如图2）：两个端点开始时刚好连在一起，这时只要将它们向上移动一点点，它们就会一左一右地分开了，这样还是三角形吗？

    图2

    生：不是。

    师：所以用10厘米、6厘米、4厘米的三根小棒——

    生：（齐）不能围成三角形。

    三、沟通图形联系时进行动态想象

    对于平面图形，教材在编排时突出了“转化”思想的渗透，然而在实际计算时学生很容易对相关图形的面积公式产生记忆混淆。分析原因，笔者以为是教材过于强调对平行四边形面积的“依赖”，忽视了平面图形之间的内在逻辑联系，缺乏从整体上沟通联系。因此，通过适当、合理的“动态想象”，帮助学生有效沟通平面图形面积之间的内在关联，形成知识网络结构，就显得非常重要。

    例如，在学习了平面图形的面积之后，我们可以安排这样的整合练习：给出高和面积一定的梯形，让学生对符合已知条件的梯形展开有效的“动态想象”，从而感悟梯形上、下底之间的关系。在不同梯形的变化之中感悟极限思想，体会不同平面图形面积公式之间的相通之处，从而突破因教材编排设计而产生的逻辑线索的束缚，形成整体性认知结构，进而感悟平面图形之间的等积变形思想和方法，理清知识脉络，形成知识网络。

    “多边形的面积”教学片断：

    你能在一组平行线（如图3）之间画出高为5厘米，面积为20平方厘米的梯形吗？（注：每一小方格边长为1?cm）

    图3

    1.生独立思考，在格子纸上画一画。

    2.组内交流。

    3.作品展示、汇报交流。

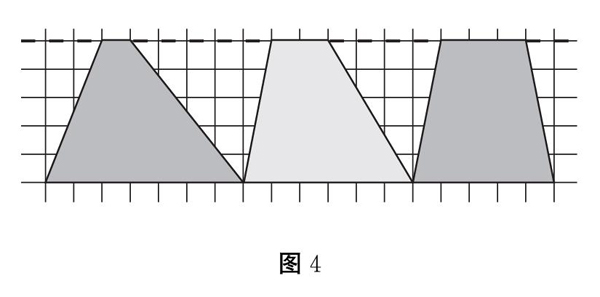
    教师课件出示不同梯形（如图4），问：请仔细观察这些上底和下底分别为1和7、2和6、3和5的梯形，你有什么发现？

    图4

    4.小组交流。

    它们的上底和下底相加的和都等于8。

    （发现梯形等积变形的本质：上、下底之和不变）

    5.“动态想象”，沟通联系。

    师：从右往左看，如果梯形的上底继续缩短，想一想会怎么变、变成怎样的图形。

    生：越来越接近三角形。

    师：大家有没有听明白她的意思？请你上台演示给大家看看。

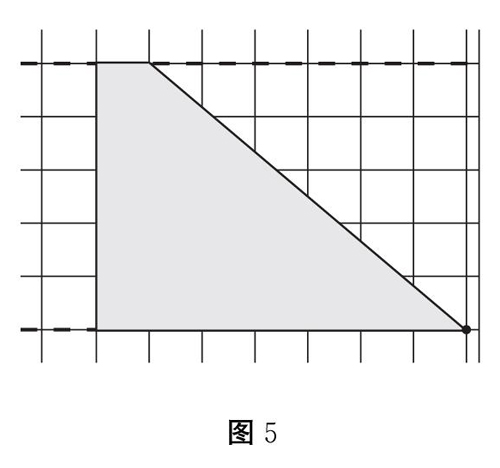
    生操作演示（如图5）

    图5

    师：在什么情况下，梯形会变成三角形？

    生：当梯形的上底越来越短，长度为0时，就会变成三角形，此时的下底刚好等于8。

    师：这时怎么计算三角形的面積？

    生：（0+8）×5÷2。

    师：也就是说，梯形的面积公式还可以用来计算三角形的面积。

    [板书：当上底=0时，三角形面积=（上底+下底）×高÷2]

    6.实时整合，建构网络。

    师（指着图4）：从左往右看，当梯形的上底不断变长，下底也就会不断变短，想象一下，梯形又会发生什么变化呢？

    生：噢！会变成平行四边形。

    师：那么，平行四边形的面积是不是也可以用梯形面积公式来计算呢？

    教师相机板书，沟通平面图形的面积关系。

    总之，空间观念看不见、摸不着，是一种印象，更是一种能力，具有一定的抽象性。我们在“图形与几何”教学中，既要处理好“动态想象”与“动手操作”之间的辩证关系，避免学生操作活动的随意性和虚假性，还要让学生有想象的材料、想象的平台、想象的时间和想象的方法。如此坚持，学生的空间观念才有持续和深入的可能，学生的思维品质才能得到有效的提升。

    参考文献：

    [1]董雪云.在“动态想象”中发展儿童的空间观念[J].江西教育，2017（12）.

    [2]江莉莉.让“动态想象”润泽小学数学课堂[J].小学教学研究，2012（6）.

    责任编辑：黄大灿