关于“弹力与弹簧伸长量的关系”的实验
徐小林
实验一、通过弹簧和钩码完成实验
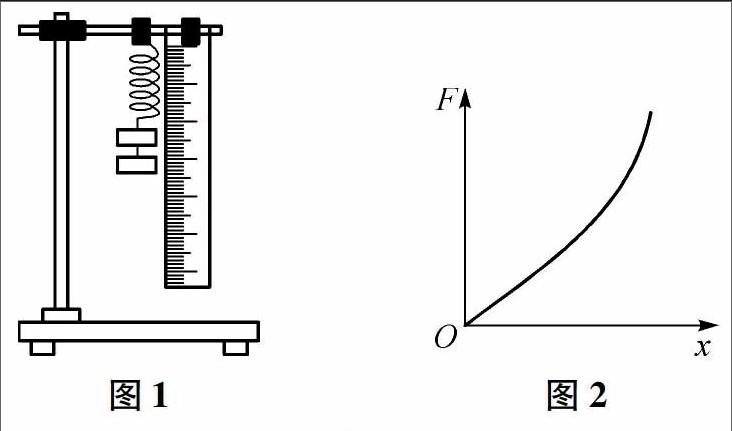
如图1所示,安装好铁架台,将一根弹簧一端固定在铁架台上,同时将刻度尺与弹簧竖直平行固定,记下此时的弹簧的长度(即弹簧的原长).在弹簧下端挂上已知质量的钩码,则弹簧的弹力等于钩码的重力,记下此时弹簧的长度,从而得到弹簧的形变量;改变钩码的个数,获得不同的弹簧拉力和形变量.把获得的数据计人表格之中,利用坐标纸画出F-x图象(x为弹簧的形变量),经过试验发现在误差允许的范围内,图象为过原点的一条直线,说明了弹力和弹簧伸长量成正比关系.具体在操作的过程中要注意刻度尺的竖直放置,所挂钩码的重力在弹簧的劲度范围之内.其实,真正完成实验得到的图象是如图2所示的曲线,其原因是胡克定律中所说的形变量是线性一维弹性体的形变量,而我们的弹簧是二维截面材料,所以形变量比较大时就不严格按照正比关系,这里只研究形变量比较小的情况下.
实验二、通过圆珠笔和砝码完成实验
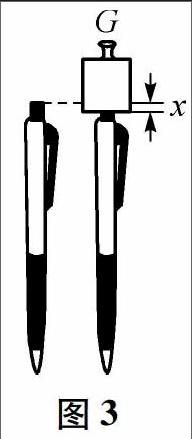
如图3所示,将圆珠笔用白色的硬纸板竖直固定,并在白色硬纸板上竖直固定刻度尺,读出网珠笔的原长.在圆珠笔上放上一个砝码,记下此时网珠笔的长度,从而得到网珠笔的压缩量;改变砝码的个数,记下不同的弹力和形变量,利用坐标纸画出F-x图象(x为弹簧的形变量),经过试验发现在误差允许的范围内,图象为过原点的一条直线,说明了弹力和弹簧压缩量成正比关系.实验发现不管弹簧压缩还是拉伸其弹力均与其形变量成正比.
实验三、通过位移和力传感器精确完成实验
上述两种实验,由于弹簧自身有重力,严格来说,测量比较的不是形变量和弹力之间的关系,应该是弹簧弹力变化量和形变变化量之间的关系.为了消除弹簧自身的影响及完成测量的连续性,可以改进如下:
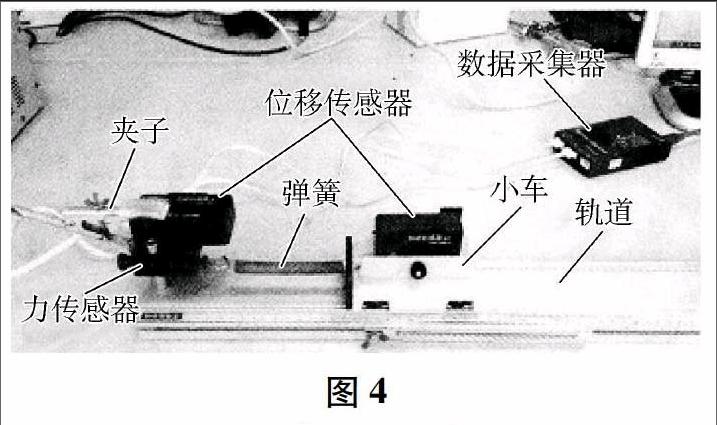
实验所需要的器材有位移传感器,力传感器,夹子,轨道,小车,数据采集器,电脑及DIS软件.按照如图4所示的安装好实验器材,将力传感器和位移传感器固定在轨道一端,力传感器与弹簧的一端相连,弹簧的另一端与小车相连接,小车上固定位移传感器的另一部分;开始让弹簧处于原长,移动小车拉伸弹簧,力传感器读出弹簧的拉力,同时小车的位移即为弹簧的形变量,将两个数据导入电脑,利用软件绘制出图象.去除离散的点,舍去前面变弯曲曲线的几个数据点,选取“直线拟合”可以得到一条直线,更加精确的验证和探究了弹力与弹簧伸长量成正比关系.此实验将将弹簧水平放置就可以克服弹簧重力对实验的影响,另外利用传感器让数据测量更加精确.



实验一、通过弹簧和钩码完成实验
如图1所示,安装好铁架台,将一根弹簧一端固定在铁架台上,同时将刻度尺与弹簧竖直平行固定,记下此时的弹簧的长度(即弹簧的原长).在弹簧下端挂上已知质量的钩码,则弹簧的弹力等于钩码的重力,记下此时弹簧的长度,从而得到弹簧的形变量;改变钩码的个数,获得不同的弹簧拉力和形变量.把获得的数据计人表格之中,利用坐标纸画出F-x图象(x为弹簧的形变量),经过试验发现在误差允许的范围内,图象为过原点的一条直线,说明了弹力和弹簧伸长量成正比关系.具体在操作的过程中要注意刻度尺的竖直放置,所挂钩码的重力在弹簧的劲度范围之内.其实,真正完成实验得到的图象是如图2所示的曲线,其原因是胡克定律中所说的形变量是线性一维弹性体的形变量,而我们的弹簧是二维截面材料,所以形变量比较大时就不严格按照正比关系,这里只研究形变量比较小的情况下.
实验二、通过圆珠笔和砝码完成实验
如图3所示,将圆珠笔用白色的硬纸板竖直固定,并在白色硬纸板上竖直固定刻度尺,读出网珠笔的原长.在圆珠笔上放上一个砝码,记下此时网珠笔的长度,从而得到网珠笔的压缩量;改变砝码的个数,记下不同的弹力和形变量,利用坐标纸画出F-x图象(x为弹簧的形变量),经过试验发现在误差允许的范围内,图象为过原点的一条直线,说明了弹力和弹簧压缩量成正比关系.实验发现不管弹簧压缩还是拉伸其弹力均与其形变量成正比.
实验三、通过位移和力传感器精确完成实验
上述两种实验,由于弹簧自身有重力,严格来说,测量比较的不是形变量和弹力之间的关系,应该是弹簧弹力变化量和形变变化量之间的关系.为了消除弹簧自身的影响及完成测量的连续性,可以改进如下:
实验所需要的器材有位移传感器,力传感器,夹子,轨道,小车,数据采集器,电脑及DIS软件.按照如图4所示的安装好实验器材,将力传感器和位移传感器固定在轨道一端,力传感器与弹簧的一端相连,弹簧的另一端与小车相连接,小车上固定位移传感器的另一部分;开始让弹簧处于原长,移动小车拉伸弹簧,力传感器读出弹簧的拉力,同时小车的位移即为弹簧的形变量,将两个数据导入电脑,利用软件绘制出图象.去除离散的点,舍去前面变弯曲曲线的几个数据点,选取“直线拟合”可以得到一条直线,更加精确的验证和探究了弹力与弹簧伸长量成正比关系.此实验将将弹簧水平放置就可以克服弹簧重力对实验的影响,另外利用传感器让数据测量更加精确.

