数形结合思想在数学教学中的渗透研究

    陈深厚

    【摘要】数形结合能够将抽象的数学理论和概念变得生动直观，可以有效避免学生的机械记忆，很好地改善学生的学习困境。因而在教学中渗透数形结合思想显得十分重要。本文通过教学中对数形结合进行分析研究，以此来渗透数形结合思想策略，为小学阶段的数学教学提供借鉴。

    【关键词】数形结合思想；以形助教；数形转化；以形促思

    数形结合的思想是一种重要的数学思想方法，是通过数与形之间的对应和转化来解决数学问题。利用数形结合能使数和形有机统一起来，以形助数、数形转化、以形促思，将生涩难懂的数学问题更直观形象地展现在学生面前，把抽象问题具体化，复杂问题简单化，不仅能够提高学生解决数学问题的能力，而且能够形成良好的数学思维，对培养小学生全面发展具有重要意义。

    一、以形助数，变被动学习为主动学习

    小学阶段的孩子心智仍处于发展阶段，对于抽象的数学概念总是感到一知半解或似懂非懂。教学中把“数字”与“图形”相结合，将抽象难以理解的概念转变为更加直观易懂的图形，有助于深化学生对知识概念的认知。方程教学是小学中高年级的难点，尤其对于解方程，含有未知数X的式子对学生而言是一个全新的知识。因此，可借助天平进行解方程知识的教学。

    二、数形转化，增强解决问题的能力

    小学阶段有关几何知识的学习都是基础的，学生对于图形的学习主要建立在实物上，即表象基础上，从而使学生头脑中模块化的知识点变成一个具有联系的整体。如图：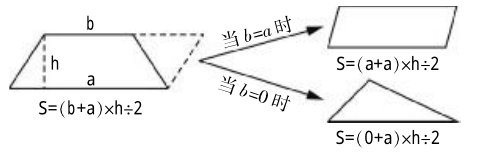

    利用知识点之间的联系，帮助学生完成对平面图形的转化和计算公式的推导，使学生掌握三者之间的关系。能够容易总结出下底a想等于上底b时，梯形转换为平行四边形；当b为0时，梯形为三角形。强化了学生的图形认知，提升了學生的空间观念，增强了学生解决问题的能力。

    三、以形促思，灵活掌握数学算理

    数学运算是学生能够灵活运用数学的解题方法和思想来解决遇到的数学问题，同时在实际的教学过程中呈现出数形属性。在讲授“多边形面积”时，首先引导学生回忆长方形、平行四边形、梯形和三角形面积的推导公式，再让学生用直尺测量的方法求出每个图形的面积。

    学生在测量中会发现面积相等的平行四边形、梯形、三角形、长方形周长不一定相等，学生在对“形”有了深刻认识的同时还灵活地掌握了数学算理。不仅煅炼了学生数学的操作能力，而且提升了学生的思维能力。

    数形结合思想是小学中高年级解决数学问题的高效方法，符合小学阶段学生的思维特点，教师在教学中应有意识地逐步渗透数形结合思想，把数形结合应用到教学中，培养学生数学学习兴趣和思维能力，对于促进和提升小学生数学学科素养具有重要作用。

    【参考文献】

    [1]王婉莹.探究小学数学教学效率的有效提升策略[J].中国校外教育，2018（16）.