遍历查找中的计算思维

2023.08.09

陈凯

机器人小睿身处一个洞穴迷宫中，迷宫中有许多空间，各个空间之间有道路相连。小睿的任务是搜集可能存在于各个空间中的能量石，并且不能有所遗漏。然而，小睿一旦出发，就必须按既定的命令以规定好的路径运行，不能临时改变方向。为了简化问题，假设迷宫中不存在回路（就是兜了一圈回到原地的路径），并且，从最开始的洞穴空间出发，只有左和右两条道路可选择，进到新的洞穴空间后，也一样只有左右两条道路可选（包含来时的道路，每个洞穴空间最多有三个方向可以走）。作为小睿的主人，应该怎样给小睿下达指令，才能比较有效地搜索整个迷宫呢？

这其实就是一个树结构的遍历问题，仔细想想，小睿的主人恐怕不是那么容易当的。一方面，他要想办法做到多快好省全，使机器人既不能错过某条路，也要尽量减少重走已探索過路径的情况;另一方面，他还要考虑如何将自己的要求编码成某种指令，用尽可能简洁明确的方式传达给机器人小睿。

或许有相当多的读者知道，可以用广度优先搜索或深度优先搜索算法来完成上述任务，但对于人工智能相关内容的初学者来说，他所面对的知识和技能的网络，可能也和迷宫一样复杂。比如说，他要知道“树”或者“图”的数据结构;为了跟踪机器人的行踪，还要知道“堆栈”或者“队列”的用法;为了将迷宫呈现出来，可能需要高维的数组或列表;为了能够让机器人自动探索路径，需要用到循环或递归;并且，更重要的是，他要能将上述所有知识和技能综合在一起，把机器人探路的程序编写出来。

然而，正如大家已经认识到的，计算思维的培养与程序算法的培养，两者间虽然有联系，但并不等同。在计算思维培养过程中，常常要关注如何对问题进行编码，如何找出形式化的方法，使得问题的解决变得自动化，最后，才是将此自动化过程用算法实现出来。而在传统的算法学习中，学习者往往是直接面对已经相当成熟的、高效的问题解决方案。所以，在计算思维培养过程的初始，就要玩一种“假装不知道”的游戏，把那些成熟的算法和程序代码搁在一旁不去看它，试着自主探索某些形式化、自动化的方案，哪怕学习者的算法和程序水平有限，也不妨碍他们自主开展探索并逐渐形成别具一格的方案。

以树结构的遍历查找为例，如何在正式推出成熟算法和程序代码之前，先行开展自主探索活动，落实提高计算思维的教学目标呢？不妨来看看下面这个涂涂画画的例子吧。

● 首先来玩画画

第一个任务是画画，用图画模拟出洞穴迷宫的环境，用画图软件就可以了，如图1所示。这个任务，其实和后续指引机器人如何行动的指令编码有关，它需要学习者对头脑想象中的环境进行抽象，将不同空间之间的关系，尽可能用简洁明了的方式呈现出来。

至于怎么在画图软件中模拟迷宫环境，办法很多，比如，画矩形当作洞穴，在画面正中间画一个矩形，然后在它左右两边各画一个矩形与中间的矩形边缘相接，由此逐渐扩展。可以看出，这实际上就是一个二叉树的结构，在对它的结构有了充分的了解之后，还可以拓展研究有更多分岔路径的结构。绘图的时候，可以有意将新接进来的矩形的左右方位设置得很明显，这是为了在后续遍历时更容易描述机器人的行进动作。

● 然后来涂颜色

第二个任务，是试着依靠颜色指引机器人如何行进。想象一下，机器人一旦从初始空间出发，就需要根据实时情况的变化，保存或变更一些信息，其后才能根据这些信息指引自己在迷宫中继续行动。本文游戏中，用五彩斑斓的颜色，来直观地展现信息的存储和变化过程。

例如，这里有一个非常简单的方案：将搜索的空间分出不同的层级，探索的第一层就是最中间的空间，也就是机器人初始所在的位置，第二层是邻近第一层空间的左侧和右侧的空间，第三层，是左侧空间的左侧空间，左侧空间的右侧空间，右侧空间的左侧空间，右侧空间的右侧空间，以此类推。

考虑如下方案A。由于空间总共有四层，所以它将用到红绿蓝黄四种颜色，若加上原本的白色，就是五种颜色，四种颜色放置在调色盘中，如果迷宫层级增加，调色盘也可相应扩充：①将正中间的空间涂成红色。②搜索所有和红色邻近的空间，涂成绿色。③搜索所有和绿色邻近的空间，涂成蓝色。④搜索所有和蓝色邻近的空间，涂成黄色。每一层涂色完毕后，就可以将调色盘最上层的颜色擦除，这样，机器人就知道下一层应该涂什么样的颜色了。

按这样的规则，可以很快将所有空间遍历完成。方案A虽然简单，但若是仔细思考一下，便会发觉有很大的漏洞，因为，这其实是要求，机器人小睿必须具有重复分身的能力，每进入一个新的空间，它就在这个空间一分为二，然后二者各自去探索左右两个路径。这样的机器人，恐怕是比较难以制造出来的。

接着，考虑如下方案B。在这个方案中，除了原本的白色，就只用到红色：①机器人由低层向高层行进，若行进到无法行进时（不再有更高层），则原路返回到最初始的空间，返回时不进行新的探测任务。②当第一层空间（也就是最初始的空间）遇到机器人第四次返回时，则变成红色。③当第二层空间（有两个空间）遇到机器人第二次返回时，则变成红色。④当第三层空间（有四个空间）遇到机器人第一次返回时，则变成红色。⑤若当前空间为白色，则探索左侧空间，否则，探索右侧空间。

这个方案也可以遍历所有空间，不过，它的规则的描述比较麻烦，除了标注颜色，还需要额外的计数器来计算机器人返回了几次，当然，这个计数器也是可以用颜色变化来实现的，但如此一来，问题解决的复杂性就大大增加了。另一个问题是，每次机器人将一条路径走到底后，就必须返回“老巢”，无法在回程时顺便探索一下其他路径，所以效率不高。另外，若是从某个空间分岔的路径多于两条，也很难基于此方案进行扩充修改。

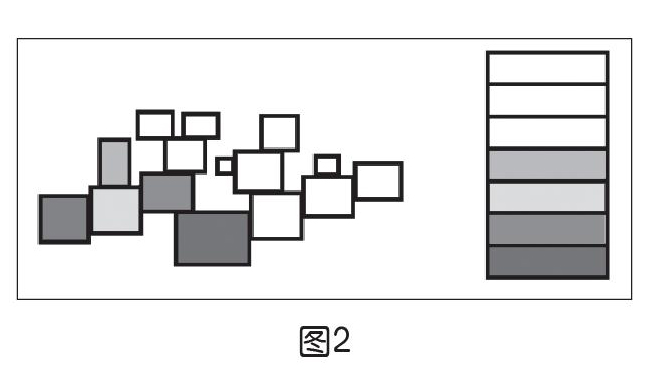
考虑如下方案C。该方案使用到十五种颜色，包含白色就是十六种，实际上，就是准备好足够多的颜色，给每个空间做一个标识。这个方案也用到了调色盘，如果层级增加，调色盘也可相应扩充：①任取一种颜色将正中间的空间涂色，然后将选取的颜色填在右侧调色盘最下一格。②任取一种颜色，对刚才所涂颜色的空间的后一层左侧空间涂色，然后将选取的颜色填在右侧调色盘中先前填色格子的上一个格子中，进入该空间，然后再执行步骤2;如不再能找到未调色的后一层左侧空间，则找到未调色的后一层右侧空间，将选取的颜色填在右侧调色盘中先前填色格子的上一个格子中，进入该空间，然后执行步骤2;若未找到后一层左侧和右侧空间，则擦除调色盘最上一层颜色（填入白色即可），然后执行步骤3。③按调色盘最上一层颜色的指示，回到当前空间的前一层空间，然后执行步骤2。

在操作过程中需要注意的是，每次擦除颜色，都只是擦除调色盘上的颜色，而不是擦除迷宫空间里的颜色。

图2是整个方案实施中的某一步。

在整个过程中，调色盘其实起到了堆栈的作用，而机器人行走的路径，则模拟了深度优先搜索的整个过程，规则指令运行起来颇为波折，但跟踪过程也很有趣味。此方案的优点是，如果遇到有更多条路径分岔的情况，也很容易修改规则来完成探路游戲。大家若有兴趣，还可以把迷宫做成棋盘，把规则指令做成积木块，把积木块打乱之后，思考怎么重新排列积木块，来指挥机器人完成迷宫探索任务。

除了上面提到的方案A、B、C，其实还有更多方案，比如，也可以不依赖调色盘来完成探路任务，这就需要用到递归，或是用并行自动机的方法，限于篇幅这里不再一一描述，给读者留一些探索空间。

● 接着来猜字谜

重新考察方案B，如果将机器人行进方向分为L和R（前进时总是往后一层，返回时总是往前一层），则可以看出，探索第二层空间时，机器人执行的是LRRL，探索第三层空间时，机器人执行的是LLRRLRRLRLLRRRLL，到了第四层的时候，全部的指令要是写出来的话就比较长了：LLLRRRLLRRLLLRLRLRLRRRLLRLLLRRRLRLRLRRLLLRRRRLLL。

其实，探索第二层空间的指令，和探索第三层、第四层空间的指令，是存在着演变变化规律的，怎么找出规律呢？

由于返回的路径总是与前进路径方向相反，所以不妨简写为“B”，于是上述指令字符串就变成了这样：LLLBLLRBLRLBLRRBRLLBRLRBRRLBRRRB。

可以看出，方案B的指令字符串的演变，其实和二进制计数器完全一致，这也说明了，为什么可以用二进制数来对二叉树的节点进行标注。

接着，再重新考察方案C，也将机器人行进方向分为L和R（这里暂时先不考虑到底是往前一层还是后一层），假如整个迷宫只有第一层和第二层空间的话，则机器人的行进方向就是LRRL，若是有三层空间，则机器人的行进方向是LLRRLRRLRRLL，如果是探索四层空间的话，行进方向的指令写出来后也比较长，不过比起方案B的指令字符串要短一些：LLLRRLRRLRRLLRRLLRRL

RRLRRLLL。

对于不同层级的迷宫，机器人探索路径的行动方向也是有规律可寻的，这个规律和一种常用的自动化过程——迭代有着密切的关系，并且，在一系列的迭代之后，实际上起到了分形的效果。方案C的指令字符串的演变规律如下：①初始字符串为LxRRxL。②将字符串中的x替换为LxRRxL，反复此过程。

但方案C与方案B不同，它还需要更多地考虑机器人在什么时候前进一层，什么时候后退一层，如果将机器人前进和后退的方向标为“U”和“D”，就形成了新的指令字符串，可以将“U--D”字符串和“L--R”字符串结合使用，来指引机器人行进，大家能看出“U--D”指令字符串中的规律吗？

两层迷宫：UDDU

三层迷宫：UUDUDDUUDU

四层迷宫：UUUDUDDUUD

UDDDUUUDUDDUUDUDDD

本期参考答案：设初始状态为UxDUxD，然后执行将x替换为“UxDUxD”的动作，反复进行迭代即可。

对此期主题有任何好主意和建议，请发送稿件至[email protected]（专栏作者）或[email protected]（杂志社）。