三维LP图解法仿真设计与实现

    李昂+++曹迎槐

    

    

    摘 要：线性规划（Linear Programming， LP）是运筹学中研究较为充分的一个重要分支，应用范围十分广泛，在经济金融、经营管理、工业生产等方面均有应用。它是研究在线性约束条件下线性目标函数极值问题的数学理论。目前对线性规划求解的方法比较成熟，常用的有单纯形法、原始对偶方法和图解法等。其中图解法可以清晰直观地展示求解过程，方便学习者掌握线性规划的概念和细节，以及对对偶原理和灵敏度分析等性质有更深地理解。虽然二维图解法实现相对简单，但三维的仿真实现目前在国内外尚属空白，论文的研究目的即为设计三维图解法仿真模拟程序，使其更好地为教学工作服务，进一步推动线性规划求解算法的发展。

    关键词：线性规划 二维线性规划 三维线性规划 图解法

    线性规划图解法

    1、线性规划

    线性规划是对一组决策变量研究在

    满足约束条件的前提下，最大化或最小化目标函数的问题，其中约束条件和目标函数均为线性函数，如：

    ■

    其中c为n维列向量，称为价格向量或成本向量；■，称为决策变量；b为m维向量，称为右端向量；A为m*n阶矩阵，称为约束矩阵。称■为可行域。线性规划的可行域为凸集。通常我们将最大化目标函数的值作为线性规划的标准形式（最小化问题可看作最大化其负函数，即■）。

    在线性规划问题中，决策变量的值称为一个解，满足所有的约束条件的解称为可行解。使目标函数达到最大值（或最小值）的可行解称为最优解。这样，一个或多个最优解能在整个由约束条件所确定的可行区域内使目标函数达到最大值（或最小值）。求解线性规划问题的目的就是要找出最优解。最优解可能出现下列情况之一：①存在着一个最优解；②存在着无穷多个最优解；③不存在最优解，这只在两种情况下发生，即没有可行解或各项约束条件不阻止目标函数的值无限增大（或向负的方向无限增大）。

    2、二维线性规划图解法

    二维线性规划图解法的求解过程为：求出并绘制可行域（凸多边形）；找出目标函数下降（上升）方向，并以此为法方向绘制一条与可行域交集非空的初始等值线；沿目标函数下降（上升）方向平移等值线，直至边界。最终等值线与可行域边界的交集作为最优解集，等值线所代表的目标函数值为最优值。

    下面我们用一个简单的二维线性规划问题说明图解法的求解过程。

    ■

    ■

    用图解法求解：

    第一步：画出可行域。以x1与x2为坐标轴作直角坐标系，根据不等式的意义求出各半平面的公共部分称为可行域。

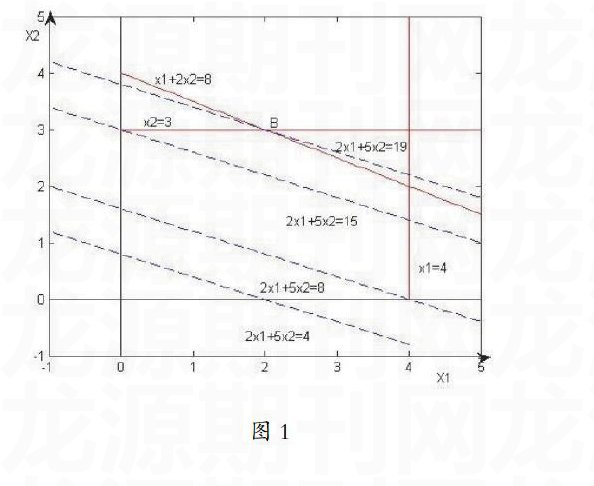
    第二步：画出等值线。目标函数S=2x1+5x2在坐标平面表示以S为参数、以■为斜率的一簇平行直线，即■，它的位置随着S的变化平行移动。位于同一直线上的所有点，都使S具有相同的值，所以该直线称为“等值线”。任取一个定点S0便可在坐标平面上画出一条等值线■，如图1所示。

    第三步：求最优解。将直线■沿其法线方向向右上方平行移动时，参变量S的值由S0逐步增大。当等值线平行移动到可行域的最后一个点B时，S达到最大值。此时由线性方程组可解得B的坐标（2，3），故目标函数的最大值S=19。

    对于二维的线性规划图解法，我们很容易在直角坐标系中实现，很容易在教学上演示，但当线性规划提升至三维乃至更高维空间以后，一些简单直观的操作就变得复杂起来，为了更好的研究和演示三维LP图解算法，需要分析图解算法的数学本质，使用精确的数学语言而非自然语言来描述图解算法。

    3、三维线性规划图解法

    三维LP图解算法在步骤上与二维的相似，但在细节上较为复杂，它的具体步骤可以简述为：

    3.1求出并绘制可行域

    根据线性规划的基本理论，一个n维空间中线性不等式组的解集一定是个凸多面体（polyhedron）。特别的，如果线性不等式组的解集有界（即对任意的目标系数向量■，有■），那么该不等式组的解集是一个多胞形（polytope）。由于图解法的特殊性和局限性，在LP图解法中，我们主要求解的是后者。

    N维空间多胞形的定义：Q是n维空间Rn中的多胞形，当且仅当Q是Rn中有限点集的凸包，i.e. ■。

    在二维平面上的图解法中，绘制可行域其实就是绘制了这个多胞形（限制在二维空间中为多边形）。而绘制多胞形所必需的信息即该多胞形的全部顶点。虽然，在理论上我们已经知道有界不等式系统和多胞形的等价性，但是这个定理的证明本身并没有提供计算多胞形全部顶点的算法。而Danzig所提出的单纯形算法理论，提供了求解这些顶点坐标的理论工具。基于多面体顶点的基本定义，可以简单的得到结论：多胞形的顶点一一对应于任一定义在这个多胞形上线性规划的基本可行解。即：

    求解给定线性不等式组对应多胞形的顶点问题等价于求解该多面体上线性规划基本可行解。

    基于这个结论，可以得到如下多项式时间的多胞形顶点坐标求解算法：

    Step1：对于给定的线性不等式组Ax≤b，考虑其增广矩阵，选取一组极大线性无关行向量组得到与原不等式组等价的不等式组■；

    Step2：选取■全部的极大线性无关列向量组，对■的每一个极大线性无关列向量组■，其实是一个满秩的方阵，■即可求得一个基本可行解，即一个顶点的坐标。遍历所有这样的■，就可以求得全部顶点的坐标。

    3.2找出目标函数下降（上升）方向，并以此为法方向绘制一条与可行域交集非空的初始等值线

    目标函数的下降（上升）方向甚至是梯度方向都是容易求解的，因为目标函数的梯度正是目标系数向量。但是寻找初始与可行域交集非空的等值线则是一件复杂的事情。事实上，初始等值线的选取问题等价于如下问题：

    找到■，使得线性不等式组{Ax≤b，cx=c0}解集非空，即寻找一个原线性规划的初始可行解。在运筹学中，两阶段法是用来构造求解初始可行解的常用手法。两阶段法简要如下：

    Step1：将线性不等式组Ax≤b化成标准型中的等式组，每一个不等式添加非负的一个人工松弛变量变量；

    Step2：构造新的目标函数，及最小化人工变量之和；

    Step3：求解该线性规划，如求得的最优解的目标函数值为0，则该最优解为原问题的可行解；如目标函数值大于0，则原问题无可行解。

    在求得初始可行解x0以后，即可选取cx=cx0为初始等值面。

    3.3沿目标函数下降（上升）方向平移等值线（面），直至边界

    在该步骤中，主要的难点在于如何判定等值面是否到达边界。一方面，由于移动的是等值面，故在图解算法过程中并不记录当前可行解的信息，所以单纯形算法所使用的检验系数判定方法难以奏效。另一方面，图解算法的移动行为非常近似于使用连续优化技巧的线性规划内点算法，所以三维图解法的边界判定算法可以借鉴连续优化的判定方法。

    在连续优化中，通常并不严格计算一个点是否落在可行域边界上，而是通过完成判定是否落在可行域内，然后通过线搜索算法逐渐逼近最值点或边界点。对应到线性规划问题上，其实就是求解如下判定问题：

    给定任意■，判断线性不等式组{Ax≤b，cx≤c0}解集上是否为空。

    线性不等式组的解存在问题可以借助Farks引理来转换成线性等式组来处理。

    Farks引理：令A是一个矩阵，b是一个向量。那么线性不等式组Ax≤b有解，当且仅当对于所有满足yA=0的行向量y，有yb≥0。

    事实上，这里就相当于求解出yA=0的全部基本可行解，并逐一判断是否满足yb≥0。

    到此为止，已经把LP图解法中每一个子问题推广到n维空间中（自然包括三维），并对每一个子问题给出了求解算法，藉此摆脱了原LP图解法的直观经验性描述而将其上升至了具有一般意义的数学算法。

    三维LP图解法的演示算法的改进

    这一章节主要研究三维LP图解的演示动画实现算法。对于动画演示，重点是体现等值面从初始位置连续移动至可行域边界的过程。由于在演示动画中，并不会显示具体的算法，所以为了提升算法的运算速度，我们可以对上文中的图解算法进行简化和改进。

    仔细分析上文中的图解算法，发现初始等值面的选取（两阶段法的第一阶段）以及边界判定（不等式组解集是否为空）的计算量都至少等于一次同等规模的线性规划算法的计算量，对于动画演示来说，其实有相当一部分的运算是无意义的，所以针对动画演算，采取如下简化算法：

    Step1：绘制可行域；

    Step2：初始点选取。以-c为目标系数，求解线性规划，以求得的最优值作为初始等值面；

    Step3：计算移动终止位置。以c为目标系数，求解线性规划，以求得的最优值作为等值面终止位置。

    Step4：从初始位置开始，直至终止位置连续绘制等值面移动动画。

    这样在整个过程中，step2和step3的运算量就压缩到了两次同规模线性规划算法的运算量，经过实验对比，在不改变动画演示效果的同时，可以极大地加快程序的运行速度。

    基于MATLAB三维LP图解法演示系统的仿真与实现

    借助MATLAB GUI设计并实现交互式的三维LP图解法演示系统。

    首先，使用edit控件设计了参数读入界面。在演示系统中，我们默认的是考虑极大化问题，且可行域限制在第一卦限，即■。并且出于简化考虑，仅考虑三个变量和三个线性不等式约束。

    在读入线性不等式以后，求出全部基本可行解，即求得可行域多胞形全部顶点坐标，通过MATLAB图形学工具箱自带的convhull，通过顶点坐标计算得到多胞形全部侧面的数据，再使用mergeCoplanarFaces函数，将共面的全部小多边形合并成大的侧面，最终完成可行区域的绘制。

    等值面移动动画通过以下方法完成，对于处于最小值和最大值中间状态的任意一个等值面cx=c0，将可行域分割成两个部分{ax≤b，cx≥c0}以及{ax≤b，cx≤c0}两个相邻接的多面体，用不同的颜色绘制，以此标注等值面。

    最后通过drawnow和pause命令生成动画，并实时显示当前可行解及其对应的目标函数值，当动画停止时所显示的即为最优解和最优值。

    在此基础上，通过改变线性规划约束中的系数我们可以实现三维线性规划图解法的动态展示。

    总结与展望

    本文在掌握了二维线性规划图解法的基本原理、方法和步骤的基础上，对多维线性规划问题图解法的实现进行了理论分析，并且对三维线性规划的图解法利用MATLAB编程，编制了仿真模拟软件。该程序可以实现对三维LP模型中各参数在一定范围内的灵活设置，将三维线性规划问题优化的整个过程通过动态效果展示，界面编排合理，使用灵活方便，作为辅助教学软件能够使学生对线性规划问题的性质有更深的理解。同时基于对多维线性规划问题实质的分析，在三维图解法程序的基础上我们也很容易扩展到三维以上线性规划问题的图解法仿真模拟，未来的研究工作可以考虑设计一个通用程序，通过自由设置问题优化空间的维数实现各维数线性规划问题图解法的动态效果展示。

    参考文献：

    [1] Alexander Schrijver， Theory of Linear and Integer Programming， John Wiley and Sons. 1998.

    [2] Frederick S. Hillier and Gerald J. Lieberman， Introduction to Operations Research， 8th edition. McGraw-Hill.

    [3] 关玉昆 三维空间线性规划问题的图解法[J]，辽宁大学学报， 1999，18卷1期。

    [4] 邓先礼，最优化技术，重庆大学出版社，1998.

    [5] 申卯兴，许进 求解线性规划的单纯形法的直接方法，计算机工程与应用，2007，30期，p94-96.

    [6] 燕子宗，费浦生，万仲平. 线性规划的单纯形法及其发展，计算数学，2007，1期.

    [7] JH. Mathews， KD. Fink. Numerical methods using MATLAB. 1999.

    [8] 张志通. MATLAB教程，北京航空航天大学出版社，2006.

    [9] 钱俊，吴金洪，程茗. 线性规划问题的MATLAB求解. 科技创新导报. 2011，25期，p158.

    [10] 龙林川， 浅谈二变量线性规划问题的图解法. 科技信息，2012，25期，p138-139.

    （作者单位：浙江省宁波市公安海警学院）