关于旋度公式的推导方法

    丁尚文 郭清伟 陈琳

    

    

    

    摘 ?要 以水漩涡为例，讨论漩涡中微元旋转强度问题。采用环流量与面积之比的极限对水漩涡中心处的微元旋转强度建立数学模型，通过数学模型求解找出速度场与旋度场之间的联系，推导出旋度概念和定义。该教学设计以水漩涡为例，借助数学建模方法培养学生解决物理问题的能力。

    关键词 水漩涡;旋度;环流量;角速度;数学模型

    中图分类号：G642 ? ?文献标识码：B

    文章编号：1671-489X（2019）18-0098-04

    Derivation Method based on Curl Formula//DING Shangwen， GUO Qingwei， CHEN Lin

    Abstract Taking the water vortex as an example， this paper discusses

    the measurement of the rotation intensity of the micro element in the

    vortex. By using the limit of the ratio of annular flow to area， a mathematical model is established to measure rotation intensity of

    the micro element at the center of water vortex. By solving the mathematical model， the relation between the velocity field and the

    rotation field is found out， and the concept and definition of the curl

    is deduced. This instructional design takes water vortex as an exam-

    ple， and helps students develop their ability to solve physical pro-blems by means of mathematical modeling.

    Key words water vortex; curl; annular flow; angular velocity; mathematical model

    1 引言

    旋度是多元函數积分学中一个重要的概念，在流体动力学、流体运动学和空气动力学等领域有着非常广泛的应用[1]。高等数学相关教材已给出旋度的概念和定义，教材设计通常是先给出环流量的密度公式，然后由环流量密度公式推导出在某一点处的旋度[2]。

    国内外学者就旋度概念的理解和公式推导做出很多研究。任京男等提出关于奇点的旋度算法[3]。黄辉等把散度和旋度这两个反映不同物理特性的物理概念加以比较，设计并实践了以散度和旋度为内容的研究型教学模式[4]。Schey等考虑矢量函数在一个小长方形上的环流量积分计算，研究结果发现，环流量比上小长方形的面积再求极限值，与旋度向量的一个分量表达式完全相同[5]。杜晓燕等把亥姆霍兹定理等知识点作为例题，帮助学生理解旋度概念和应用[6]。黄国良等从流速场角度出发，详细地说明了矢量场旋度的物理意义[7]。李黎等研究结果表明，旋度在变形体的速度场中仍然存在矢量场的旋转特性[8]。徐亮等采用旋度公式对旋转冲击射流传热特性开展研究，结果表明，内置螺旋杆产生的旋流在靶标面上具有均匀高效换热性能[9]。

    上述文献研究主要工作在旋度定义的理解和相关例子的补充上。旋度概念的产生在教材中较少出现，以及如何根据实际问题推导出旋度公式，这些问题仍然需要进行进一步补充和推导证明。

    本文以物理现象水漩涡为例，阐述旋度概念的产生和公式的推导。旋度公式的推导首先从自然现象漩涡直观认识出发，提出漩涡中某处微元的旋转强度如何计算问题;其次，采用环流量与面积之比的极限对微元旋转强度建立数学模型;最后，通过数学模型求解找出速度场与旋度场之间的联系，推导出旋度公式。

    2 漩涡中微元旋转强度建模

    背景 ?生活中遇到的漩涡例子很多，如水漩涡、风漩涡、飞机的尾部产生的气流漩涡。漩涡的形状如图1所示。如何度量水漩涡旋转强度？对此需要建立数学模型。为了分析简单化和形象化，可以假设水漩涡某处有一个微元，该微元的旋转强度与水漩涡的旋转强度相同，度量水漩涡的旋转强度间接转化成度量微元的旋转强度。

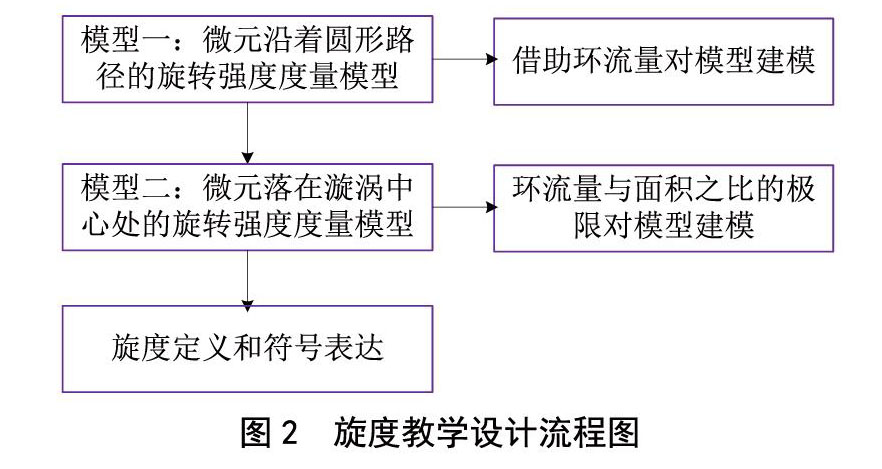
    本文首先对漩涡中某微元在某处的旋转强度建模。第一个数学模型是关于微元绕着圆形路径旋转一周的环流量的计算模型。该模型简单、直观，学生能够想到用微元的环流量来度量水漩涡的旋转强度。随着问题的深入，如果漩涡中的微元循着螺旋路径逐渐卷入漩涡中心，如何度量水漩涡中心位置处微元的旋转强度？由此可以看出，该模型被用来度量微元在某一点处的旋转强度显然不准确。在此基础上，采用环流量与面积之比的极限对微元旋转强度建立数学模型，通过数学模型求解找出速度场与旋度场之间的联系，给出旋度概念。本文建模设计具体流程如图2所示。

    问题分析 ?图1中的漩涡在旋转时与角速度有关，可以用右手法则确定角速度的方向，水漩涡的方向可规定与角速度的方向一致。假设水漩涡某处存在一个微元，该微元随着漩涡在旋转，微元沿着圆形路径旋转一周的环流量可以描述漩涡整体旋转强度。微元沿着螺旋线型的路径运动，微元逐渐被卷入水漩涡中心。微元在水漩涡中心处的旋转强度不能够单独用环流量来描述和进行定量分析。如何解决微元在某一点处的旋转强度？该类问题解决首先需要分析微元旋转与哪些因素有关，具体见表1所示水漩涡旋转强度相关变量表。

    根据表1中的相关变量可以发现，微元在水漩涡中的旋转强度与角速度、圆形半径和环流量有关，水漩涡旋转强度的方向可以规定与角速度的方向相同。

    模型假设

    1）研究水漩涡旋转强度，假设一个微元处在漩涡中，该微元的旋转强度与漩涡的旋转强度一样。

    2）假设微元运动的角速度与漩涡旋转的角速度大小相同。

    3）为了简化微元在水漩涡中运动的轨迹路线，微元在水漩涡中旋转一周的轨迹路线为圆形路径。

    4）假设微元运动的线速度、角速度与微元在水漩涡中的位置有关。

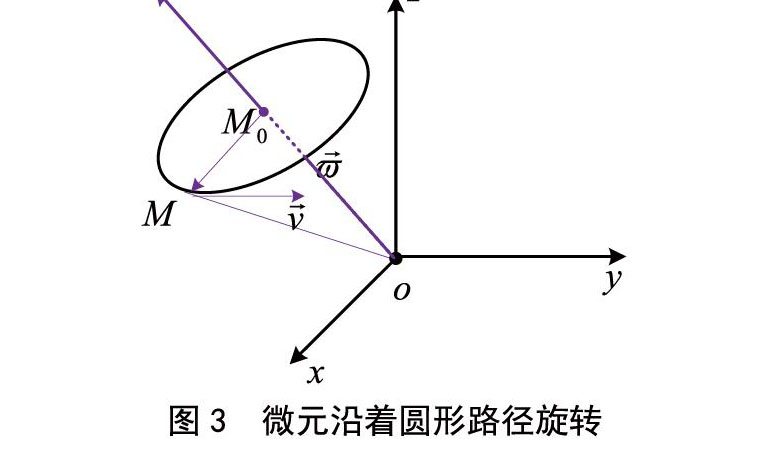
    模型建立 ?以水漩涡为例，对漩涡中某一微元旋转强度建立数学模型。度量水漩涡强度首先考虑微元旋转一周的环流量。假设微元在水漩涡中随着漩涡在做旋转运动，微元旋转运动假设为圆周运动（注：为了环流量的计算简单，将数学模型简单化）。微元循着圆形路径转动的角速度的坐标设为。圆形路径中心点位置M0坐标设为（x0，y0，z0），微元某一时刻在圆形路径中的位置M的坐标设为M（x，y，z），具体位置如图3所示。

    则微元在A（x，y，z）点的线速度为：

    其中。

    水漩涡中的微元沿着圆形路径旋转一周的环流量为：

    通过公式（4）得出在单位时间内沿着空间曲线Γ的指定方向流过封闭曲线的流量，它的大小体现了空间曲线Γ所围成的曲面Σ上的整体漩涡强度。如果微元运动到漩涡中心，要度量水漩涡中心位置处的微元旋转强度，显然环流量不够充分。

    漩涡中心位置处的漩涡旋转强度可以借助圆形路径Γ张成的曲面Σ面积（?Σ=Γ）趋近于零的极限来描述该点处的微元在水漩涡中心处的旋转强度：

    模型求解 ?公式（4）中微元绕圆形路径环绕一周的环流量可以通过斯托克斯公式化简为[2，10]：

    其中

    利用对面积的曲面积分中值定理可知，至少存在一点（ξ，η，ζ）∈Σ，有：

    根据公式（8）和（14），可以得到漩涡中某微元在M（x，y，z）点处旋转强度Φ的计算公式为：

    旋度定义产生分析 ?公式（14）漩涡中某微元在M（x，y，z）点处旋转强度Φ还可以用向量内积表示为：

    通过公式可以进一步发现漩涡中某微元在M（x，y，z）点处旋转强度Φ可以理解成新向量在法向量上的投影。综上，微元在某处的旋转程度可以用这个新向量来描述，故该新向量命名与旋转有关，将其命名为旋度。

    抽象的旋度定义：由于这个新向量产生是从水漩涡建模分析开始，结论与角速度有关联，因此命名时考虑到涡旋强度的形象表達，还要注意与角速度有区别。微元在某处的旋转程度用这个新向量来描述比较恰当，故该将其命名为旋度。抛开物理背景，给出旋度的具体定义。

    旋度定义[5，10]：设向量场，其中P（x，y，z），Q（x，y，z），R（x，y，z）具有一阶连续偏导数，点M（x，y，z）为场内一点，为向量在点M（x，y，z）处的旋度，记作。

    思考（1）：旋度是度量微元在某点处的旋转强度，角速度不能度量微元的旋转强度。

    本文建立的数学模型可以用角速度和径向量的叉积表示线速度，因此，新向量，是角速度的二倍。如果是非速度场产生的某点处的涡旋强度，就没有角速度倍数关系，甚至这个新向量与角速度没有直接联系。因此，微元在某处的旋转强度用这个新向量表达更合适。

    即使是线速度场，仍然不能用角速度度量微元在某处的旋转程度。如以水流速度是否使得水中微元旋转为例进行分析。设水流的速度场为，任意一点处的水流速度方向没有改变，但是随着水流的位置不同，速度的变化与位置的横坐标有关。若将木制圆盘置于流水中，撞击木制圆盘的流速不全部相同。由于冲击木制圆盘的速度不同，木制圆盘边缘处产生一个净扭力，因此，木制圆盘发生转动。如图4所示，水流使得木制圆盘旋转起来。

    如果要度量水流中某一点处的旋转程度，可以发现这个旋转程度与角速度没有联系，而与水流速场产生的旋度场有关。在水流在每一点处均会有旋度，

    此时的旋度分量与水流在该点处的位置有关，与角速度无关。

    思考（2）：相关教材[2]将公式（5）称为向量场在点M（x，y，z）沿法向量的环流量密度。通过公式推导，最后由公式（14）可以发现，公式（5）结果不能保证该值非负。本文将公式（5）描述成该点处的微元在漩涡中心处的旋转强度是合理的。

    3 结语

    本文以物理现象水漩涡为例，对漩涡旋转强度展开讨论，教学设计中引入数学建模分析方法给出旋度概念。本文的研究结果表明，旋度用来测量微元在某一点处的旋转强度，旋度场的产生与其相对应的向量场有关。

    参考文献

    [1]刘志军，刘凤霞，等.涡旋波流场的涡量测试与计算及特征参数的影响[J].应用力学学报，2007，24（1）：6-10，169.

    [2]朱士信，唐烁.高等数学（下）[M].北京：高等教育出版社，2015.

    [3]任京男.关于场论中旋度的两个重要问题[J].上海海运学院学报，1993，2（2）：58-63.

    [4]黄辉，张小青.“电磁场”课程的散度和旋度研究型教学例析[J].电气电子教学学报，2011，33（3）：99-102.

    [5]斯彻.散度、旋度、梯度释义[M].北京：机械工业出版社，2015.

    [6]杜晓燕，张秀钢，陆杰青.关于散度和旋度教学的几点思考[J].电气电子教学学报，2016，38（5）：81-83.

    [7]黄国良，王瑞平，舒秦.矢量场散度和旋度的物理意义[J].西安矿业学院学报，1993，24（1）：71-77.

    [8]李黎，张晓梅.旋度的一个物理解释[J].中州大学学报，1995，12（2）：70-71.

    [9]徐亮，兰进，王明森，等.旋度对旋转冲击射流传热特性的影响[J].吉林大学学报：工学版，2018，48（5）：1483-1491.

    [10]同济大学数学系.高等数学（下）[M].北京：高等教育出版社，2007.

    [11]孙逊，孙麟德.自由水涡内旋度检测的数学方法探讨[J].数学的实践与认识，2015，45（1）：127-131.

    [12]杨时中.讲授梯度与旋度概念的体会[J].西安工业大学学报，1983（1）：85-93.