课堂是一道无法预约的风景

    

    

    

    ● 创新整合点

    第一，打破传统，翻转铸就高效。本节课的重难点是利用面积法探索勾股定理，如果直接用课本上给出的“方格纸”进行探究，学生有一定的困难，我们利用翻转课堂，通过直观的、学生乐于接受的拼图活动，让学生依托自主学习任务单和微视频资源进行探索，符合学生的认知规律。

    第二，基于活动，打造体验式数学课堂。我们设计了三个递进式的学习任务——任务一：折纸，记录童年多彩的梦。要求学生通过折纸，将手中的正方形卡纸分成全等的四部分，任务设计开放，有利于发散学生思维，彰显学生个性;任务设计具有层次性和发展性，利用两张卡纸得到的“八个全等的等腰直角三角形”为任务二提供学习资源。任务二：揭开等腰直角三角形中的秘密。有了任务一的学习，学生利用拼图可以轻松解决等腰直角三角形三边平方之间的关系。任务三：自主学习，绽放精彩。

    第三，思维拓展，提升数学素养。勾股定理的探究方法多样，课前我们利用拼图法进行探究，课上主要是利用“方格纸”，从特殊到一般进行探究，有了课前的自主学习，对于一般直角三角形三边关系的探究，学生除了想到用方格纸以外，很自然地就能想到用勾股弦图进行探究，这样的设计不仅对教材进行了拓展，而且为下一节课学习勾股定理的证明奠定了基础。

    ● 教材分析

    《探索勾股定理》是鲁教版七年级第三章第一节的内容，学生在之前已学习了三角形、等腰三角形、全等三角形等有关知识，勾股定理揭示了直角三角形三边之间的关系，将形与数密切联系起来，多种数学思想在本节中得以体现。同时，勾股定理又是对学生进行爱国主义教育的良好素材，因此具有相当重要的地位和作用。

    教学重点：勾股定理的探索及简单应用。教学难点：通过面积法发现勾股定理。

    ● 学情分析

    七年级学生经过一年的几何学习，已初步具有几何图形的观察能力、几何证明的理论思维能力，但他们的数学活动经验积累较少，他们希望教师能创设便于观察的几何环境，满足他们的创造愿望，让他们实际操作，获得施展创造才能的机会。所以，本节课通过学生小时候喜欢的折纸、拼图等活动去探索，符合学生的认知规律。

    ● 教学目标

    知识与技能目标：经历不同方式探索勾股定理的过程，由特殊到一般猜想结论，并能用勾股定理解决简单的问题。

    过程与方法目标：经历“观察—猜想—归纳”的数学过程，并从中体会数形结合及从特殊到一般的数学思想，培养观察、比较、分析、推理的能力。

    情感态度与价值观目标：介绍我国在研究勾股定理方面取得的伟大成就，激发热爱祖国与热爱祖国悠久文化的思想感情，培养民族自豪感，在探索问题的过程中，培养合作交流意识和探索精神。

    ● 教学过程

    1.课前自主学习

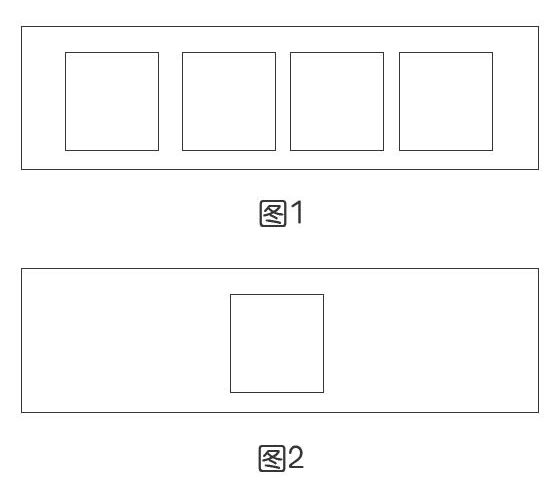
    任务一：折纸，记录多彩的童年。先按照清单准备好课前素材，然后跟随“任务一”视频完成要求的剪纸任务。准备清单：正方形卡纸10张、直尺、剪刀。动手将图1中的正方形卡纸分成全等的四部分，记录你的分割方法，再将两张卡纸分别剪成四个全等的等腰直角三角形。

    任务二：揭开等腰直角三角形里的秘密。先跟随“任务二”视频完成自主学习，然后填写以下知识清单。

    知识回顾：有一个角是_____的等腰三角形，叫做等腰直角三角形。等腰直角三角形两底角_____，等于_____。任意三角形三边关系为_____。探索新知：若等腰直角三角形两腰长为a，那么以斜边为边做正方形，正方形的面积为_____。自主探究：等腰直角△ABC中，∠C=90°，CA=CB=a，AB=c，则a2，c2的关系为_____。

    任务三：自主学习，绽放精彩。跟随“任务三”视频走进勾股定理，按提示准备好两组直角三角形以后，再开始后续的学习。观看学习完“任务三”视频以后，完成以下自主学习任务。

    ①在如图2的正方形中，设计一个“赵爽弦图”。

    ②直角三角形两直角边分别为3厘米和6厘米，用兩种不同的拼图方法，求斜边的平方，画出草图，写出求解过程。

    ③归纳总结（根据前面探究的数据填空）。

    直角△ABC中，∠C=90°，当a=10，b=10时，c2=_____，a2+b2=_____，a2+b2与c2的关

    系_____;当a=3，b=40时，c2=_____，a2+b2=_____，a2+b2与c2的关系_____;当a=3，b=6时，c2=_____，a2+b2=_____，a2+b2与c2的关系_____。

    ④猜想。

    a.直角△ABC中，∠C=90°，则两直角边a，b和斜边c的关系为_____。

    b.如下页图3所示，直角△ABC中，∠C=90°，以直角三角形的三边向外作正方形，则三个正方形面积S1，S2，S3的关系为_____。

    2.课堂教学过程

    （1）课始检测

    ①求下页图4、图5中字母所代表的正方形的面积。

    ②下页图6的图案是我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”。此图案的示意图如下页图7所示，其中四边形ABCD和四边形EFGH都是正方形，△ABF，△BCG，△CDH，△DAE是四个全等的直角三角形。若BF=6，AF=8，则AB的长为_____。

    （2）进阶作业

    ①已知直角三角形的两边求第三边的长度（如图8、图9）。

    2.如图10中，∠ACB=90°，AB=16，则正方形ADEC和正方形BCFG的面积和为（）。

    A.16? ? B.32

    C.160? ?D.256

    （3）协作探究，主题：利用方格纸探索勾股定理

    ①如图11、图12，直角三角形三边的平方分别是多少？它们满足“自主学习任务单”上关于三边平方关系的猜想吗？你是如何计算的？与同伴进行交流.

    ②如果直角三角形的两直角边分别为1.6个单位长度和2.4个单位长度，上面所猜想的数量关系还成立吗？说说你的观点，并与同伴进行交流。提示：可以借助“勾股弦图”利用拼图解决，也可以将0.8厘米看作方格纸中的单位长然后借助方格纸进行探究。

    （4）课堂小结：颗粒归仓

    ①观看“郑州科技馆”的科学小实验，发现科技馆里的秘密：_____。

    ②综合实践作业。

    a.中国古代还有哪些著名的数学发现：_____。

    b.勾股定理的证明方法有哪些呢？_____。

    ● 教学反思

    教育家陶行知曾说过，“最好的课堂不在学校，而在生活”。本节课将一部分学习任务进行“前移”，让学生课前进行充分探究，积累一定的数学活动经验，掌握用拼图法探究勾股定理。因此，在课堂教学过程中留出了充分的时间进行内化和拓展，在“协作探究”环节给予学生充足的时间和充分的思维点拨，学生的解决策略也是异彩纷呈，教学活动成为师生共同创造、即兴发挥的过程。同时，通过兄弟团队的指导和建议，我们也发现了教学设计中的一些不足，在视频资源的互动性、问题设计的层次性上有了进一步的提升，使整个课堂成为师生激情与智慧绽放的舞台。

    ● 设计亮点

    第一，采用翻转课堂的模式，提高课堂效率，更好地发展学生的数学核心素养。学生在课前依托微视频和自主学习任务单进行自学，通过剪拼过程经历勾股定理的探索过程，一方面为课上利用方格纸进行探索留下充足的时间，另一方面提高了动手实践能力，積累了数学活动经验。

    第二，创新性地整合教材。本节课采用的翻转课堂的模式，不是简单地将本节的知识前移，而是从学生的学情出发，让学生提前感知第二课时的经典图形“勾股弦图”，为后面的学习打下基础。

    第三，微视频的设计色彩亮丽，充满童趣，能够充分调动学生学习的兴趣。多彩的折纸、丰富的拼图，一下子就将学生拉回到了充满童趣的童年，学生动手操作的积极性被充分调动起来。

    第四，自主学习任务单的设计层次鲜明，注重发展学生思维的广度和深度，不是对视频内容的简单记录，而是需要学生进一步的思考和提升。

    第五，爱迪生说：“惊奇是科学的种子。”通过连线郑州科技馆，将科学实验引入数学课堂，开拓学生视野，培养学生的科学创新精神，激发学生渴求知识的欲望。