Simulink软件在混沌系统滑模控制实验中的应用

    赵海滨 于清文 颜世玉

    

    

    

    摘 ?要 对于三阶Jerk混沌系统，采用滑模控制器进行平衡控制。在滑模控制器的设计中采用线性滑模面和指数趋近律。采用双曲正切函数代替符号函数，用于削弱抖振的影响。通过Simulink软件建立仿真实验系统，滑模控制器能够进行混沌系统的平衡控制。该仿真实验有助于学生对系统仿真、混沌控制和滑模控制的理论理解和工程应用。

    关键词 滑模控制;混沌系统;Simulink;仿真实验;MATLAB

    中图分类号：G642.423 ? ?文献标识码：B

    文章编号：1671-489X（2019）18-0033-04

    Application of Simulink Software in Sliding Mode Control Ex-periment of Chaotic System//ZHAO Haibin， YU Qingwen， YAN Shiyu

    Abstract For the third order Jerk chaotic system， the sliding mode controller is used for balance control. Linear sliding surface and ex-

    ponential reaching law are used in the design of sliding mode con-

    troller. The hyperbolic tangent function is used instead of the sign

    function to weaken the effect of chattering. The simulation experi-ment system is built by using Simulink software， the sliding mode

    controller can balance the chaotic system. The simulation experiment

    is helpful for students to understand the theory of system simulation，

    chaos control and sliding mode control and to apply it in engineering.

    Key words sliding mode control; chaotic system; Simulink; simula-tion experiment; MATLAB

    1 引言

    混沌是一种看似充满随机性，而又满足某种确定性的规律，它是确定性系统中存在的随机概念。混沌可以用确定的动力学方程来表示，是非线性系统普遍存在的现象，广泛存在于自然界和人类社会中[1]。混沌系统对初始条件极其敏感，具有整体稳定、局部不稳定的非线性动力系统。基于混沌系统的保密通信具有广阔的应用前景，是非线性科学领域的研究热点。目前，越来越多的院校将混沌理论引入实验教学中，如蔡氏混沌电路的同步控制实验。混沌系统的控制和应用是当前人们研究的一个热点问题。混沌系统的同步控制已經在保密通信和图像加密等领域取得广泛应用。Jerk混沌是典型的三阶严反馈混沌系统[2]，只采用单一的控制器就能进行系统的平衡控制。Jerk混沌系统的特点是微分方程的形式简洁，能够通过硬件电路实现[3]。

    滑模变结构控制是现代非线性控制领域中的一种重要方法，具有很强的鲁棒性、构造过程简单和应用范围广等特点，广泛应用于电机控制、机器人控制、飞行器控制和混沌控制等行业。滑模控制对建模不确定和外部干扰信号具有鲁棒性，同时具有算法简单和可靠性高等优点，对非线性系统的控制具有良好的控制效果[4]。

    本文采用Simulink软件建立Jerk混沌的滑模控制仿真实验系统。在滑模控制器的设计中，采用线性滑模面和指数趋近律。指数趋近律具有非常快的收敛速度，在接近滑动模态时会出现抖振现象。在滑模控制器的设计中，为了抑制抖振现象，采用双曲正切函数代替符号函数，双曲正切函数为连续函数。该仿真实验非常形象和直观，只需要编写很少的程序代码，就能实现复杂的控制功能，能够激发学生的学习兴趣，有助于学生对系统仿真、混沌控制和滑模控制的理论理解和实际应用，有助于学生开展探索性学习，发挥学生的积极性和自主性。

    2 Jerk混沌系统

    自从1963年Lorenz发现混沌吸引子以来，人们逐渐认识到自然界和人类社会中广泛存在混沌现象。Jerk系统是美国物理学家Sprott基于计算机穷举法所提出的一种三阶自治混沌系统。对三阶Jerk混沌系统的研究引起国内外学者的广泛关注。Jerk混沌系统的特点是方程形式简洁，能够通过电阻、电容和集成运算放大器等硬件电路实现。Jerk混沌系统的状态方程是典型的三阶严反馈系统[2]，只采用单一的控制器就能进行系统的平衡控制。Jerk混沌系统具有三个状态变量，但是只采用一个控制器就能实现系统的镇定控制，因此在保密通信中具有广泛的应用价值。

    Jerk混沌是典型的三阶混沌系统，其状态方程表示为：

    其中，f1（x）=sgn（x1）+sgn（x1+2）+sgn（x1-2），x1、x2和x3是Jerk混沌系统的状态变量。Jerk混沌系统会产生四涡卷混沌吸引子。

    根据Jerk混沌系统的状态方程，采用Simulink软件进行系统的建模和仿真，采用ode45算法。ode45算法即四阶—五阶Runge-Kutta算法，是一种自适应步长的常微分方程数值解法。Jerk混沌系统状态变量x1和x2的二维相图如图1所示，状态变量x1和x3的二维相图如图2所示。由图1和图2可以观察到，Jerk系统产生了四涡卷混沌吸引子。

    3 滑模控制器的设计

    其中，k1为常数，且k1>0。采用线性滑模面的滑模控制器将系统的滑模控制分为趋近模态和滑动模态。系统从任意的初始状态趋向滑模面的过程称为趋近模态，系统在滑模面上的运行过程称为滑动模态。系统到达滑动模态后，状态变量渐进收敛到零。

    高为炳教授采用趋近律的概念，提出滑模控制系统的抖振抑制方法。在滑模控制器的设计中，常用的趋近律有等速趋近律、指数趋近律、幂次趋近律、快速幂次趋近律和双幂次趋近律等。采用幂次趋近律、快速幂次趋近律或双幂次趋近律进行滑模控制器的设计，控制输入不会出现抖振现象，但是状态变量不能收敛到零，而是收敛到稳态误差的界内。

    在滑模控制器的设计中采用指数趋近律。指数趋近律的表达式为：

    根据Jerk混沌系统的状态方程，采用线性滑模面和指数趋近律设计滑模控制器，并采用滑模控制器进行Jerk混沌系统的镇定控制。通过李雅普诺夫稳定性理论对系统的稳定性进行证明，滑模控制器能够进行Jerk混沌系统的镇定控制，状态变量渐进收敛到零。

    在公式（5）的滑模控制器中存在符号函数，当滑模面为零时，会出现抖振现象。抖振通常影响系统控制的精确性，会增加系统的能耗，而且可能激发系统中高频未建模部分的强烈振动，甚至使系統产生振荡或失去稳定。抖振的抑制和削弱成为滑模控制研究中的重要课题。为了削弱抖振的影响，在滑模控制器中采用双曲正切函数代替符号函数。双曲正切函数是连续函数，其表达式为：

    4 仿真实验

    MATLAB软件具有强大的数学运算能力，以及方便实用的绘图功能，而且对问题的描述和求解符合人们的思维习惯和数学表达习惯，已经成为虚拟仿真实验普遍采用的辅助设计工具。采用MATLAB软件可以非常方便灵活地建立复杂的系统，而且程序代码比较短，容易实现。Simulink是MATLAB软件的重要组成部分，功能强大、使用简单方便，是一种有效的可视化仿真环境[5]。在Simulink仿真环境下，可以快速建立动态系统的框图模型，不需要编写大量的程序。只需要调用各个库中提供的模块，就可以建立复杂的仿真实验系统。

    在采用Simulink软件进行建模和仿真时，通过普通Simulink模块建立系统的仿真模型不是非常直观。采用用户自定义功能模块库中的MATLAB Function模块可以非常容易地建立仿真模型，该模块内的代码可以直接采用MATLAB

    语言编写[6]。仿真实验系统运行后，仿真结果可以通过Simulink软件的示波器进行显示，也可以将数据保存到软件的工作空间中以便进一步分析。

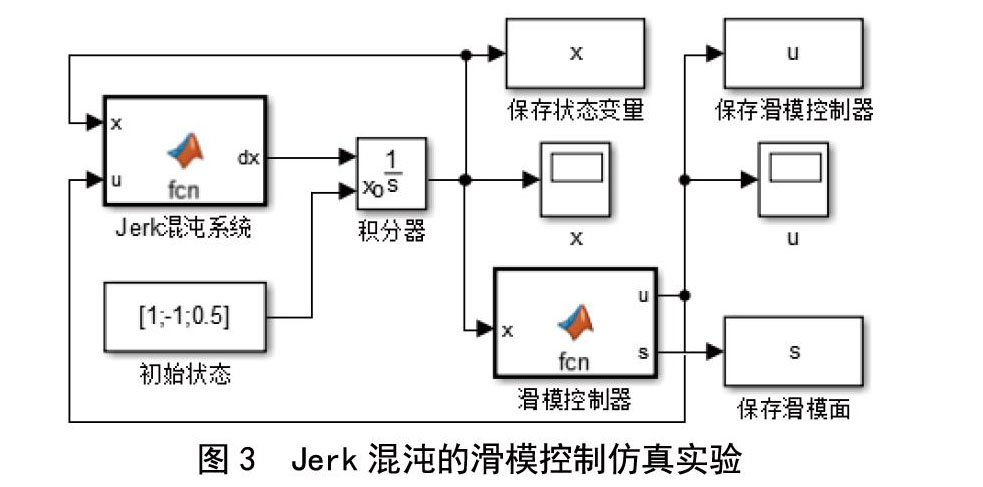
    根据Jerk混沌系统的状态方程和滑模控制器方程，采用Simulink软件建立Jerk混沌的滑模控制仿真实验系统，如图3所示。

    在图3中，主要采用MATLAB Function模块和积分模块等。MATLAB Function模块直接采用MATLAB语言建立模型和控制算法[7]，非常灵活和方便。在仿真实验中，采用变步长的四阶—五阶Runge-Kutta算法，最大步长设定为0.000 1 s，仿真时间设定为4 s。Jerk混沌系统的初始状态设置为x1（0）=1，x2（0）=-1，x3（0）=0.5。在线性滑模面公式中，参数设定为k1=6。在指数趋近律中，参数设定为k2=2，k3=1。在双曲正切函数中，参数设定为δ=0.001。

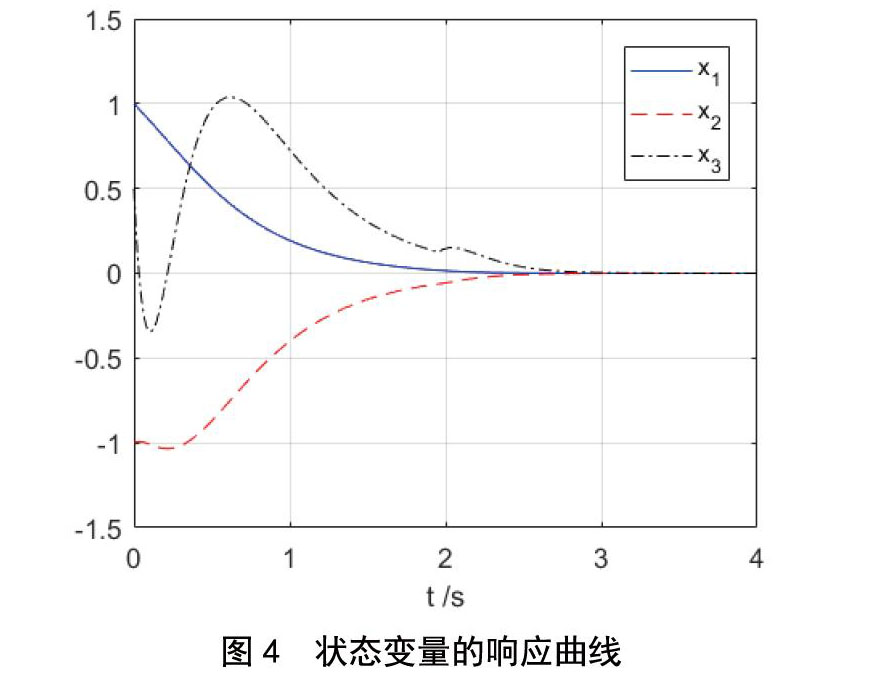
    采用滑模控制器进行Jerk混沌系统的平衡控制，仿真实验系统运行后，状态变量的响应曲线如图4所示。在图4中，Jerk混沌系统的状态变量渐进收敛到零。

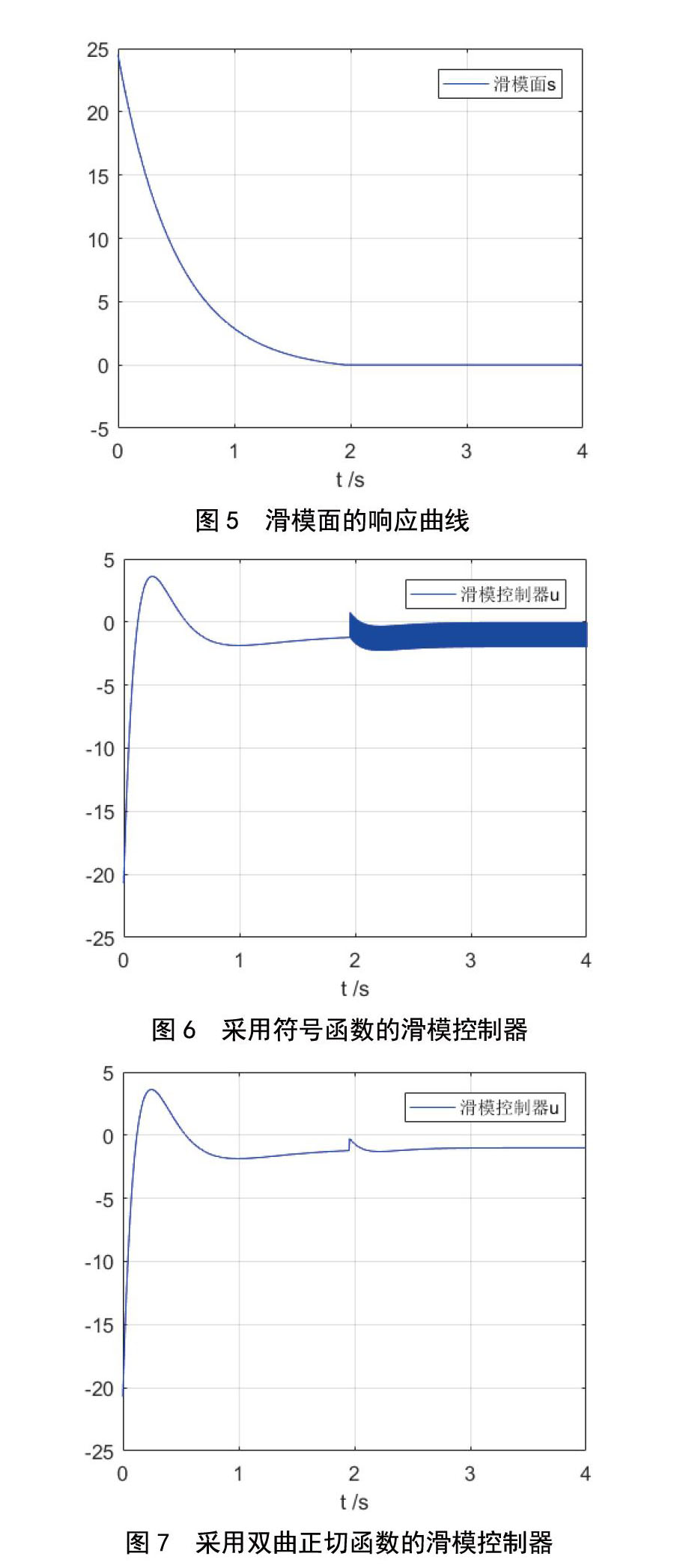
    滑模面的响应曲线如图5所示，滑模面的初始值为24.5，滑模面快速收敛并在1.95 s基本收敛到零。

    采用符号函数时滑模控制器的响应曲线如图6所示，采用双曲正切函数时，滑模控制器的响应曲线如图7所示。在图6中，滑模控制器出现抖振现象。抖振不仅会影响控制的精确性、增加能耗，而且可能激发系统中高频未建模部分的强烈振动，对系统造成危害。在图7中，滑模控制器比较平滑，没有出现抖振现象。

    仿真结果表明，滑模控制器能够进行Jerk混沌系统的平衡控制，状态变量渐进收敛到零，采用双曲正切函数代替符号函数能够抑制抖振现象。

    5 结语

    本文采用滑模控制器进行Jerk混沌系统的平衡控制，通过Simulink软件建立仿真实验系统。在滑模控制器的设计中，采用线性滑模面和指数趋近律。为了削弱抖振的影响，采用双曲正切函数代替符号函数。仿真结果表明，滑模控制器能够进行Jerk混沌系统的平衡控制，状态变量渐进收敛到零。通过Simulink软件建立仿真实验系统，方便学生动手操作，使学生更易于修改实验模型，有助于学生对系统仿真、混沌系统和滑模控制的理论进行理解并实现工程应用，有助于学生开展探索性学习，发挥学生的积极性和自主性。

    该仿真实验非常形象和直观，只需要编写很少的程序代码，就能实现复杂的控制功能。学生可以将该仿真实验作为参考，对其他混沌系统进行建模和分析，从而激发学习兴趣和创新精神，培养编程能力和工程意识。

    参考文献

    [1]孙克辉.混沌保密通信原理与技术[M].北京：清华大学出版社，2015.

    [2]俞清，姜盼，陆菱，等.基于Jerk形式的多涡卷混沌电路[J].常州大学学报：自然科学版，2016，28（2）：83-87.

    [3]吕恩胜，张绘敏.一种n-涡卷Jerk系统及其电路设计[J].贵州师范大学学报：自然科学版，2014，32（6）：76-80，84.

    [4]刘金琨.滑模变结构控制MATLAB仿真基本理论与设计方法[M].3版.北京：清华大学出版社，2015.

    [5]石良臣.MATLAB/Simulink系统仿真超级学习手册[M].北京：人民邮电出版社，2014.

    [6]赵海滨，于清文，刘冲，等.基于Matlab/Simulink的混沌同步控制实验[J].实验室研究与探索，2019，38（1）：16-19.

    [7]赵海滨，刘冲，陆志国，等.基于Matlab/Simulink的欠驱动机械臂仿真实验[J].实验技术与管理，2018，35（6）：

    135-138，143.