错中明辨　“倍”加深刻

    

    

    

    摘 要：在数学课堂上，每名学生对知識的理解不同，“生成性错误”的出现是不可避免的，教师需要在课堂上聆听学生不同的声音。特别是当“错点”出现时，教师需要拥有一双智慧的眼睛，能够将这些错误变为宝贵的教学资源，进行巧妙的引导，让学生不断发现、思考、探究，将“错点”转化成“亮点”，从而内化成学生自身的知识，提升学生的思维品质。

    关键词：小学数学;教学实践;“倍的认识”

    中图分类号：G42? ? ? ? ? ? ? ? ? ? ? ? 文献标识码：A? ? ? ? ? ? ? ? ? ? 文章编号：2095-624X（2020）16-0067-02

    引 言

    “倍的认识”作为具体形象思维与抽象思维之间的重要纽带，其知识生长点是乘法与除法的意义，它在分数、百分数、比和函数的学习中发挥着重要作用[1]。“倍”是小学数学中一个相对抽象的概念，其本质是两个量之间的比率，也就是说，先确定一个标准量，再判断另一个量中包含这样的几个标准量，即几倍。但学生容易出现倍的认知结构错误，学生如果能够在错误中明辨数学概念，正确地形成和理解数学概念，将会对概念的建立“倍”加深刻。

    一、抓住错误，让“倍”的构建过程更自然

    【教学片段1】

    师：学校里要布置教室，我们班打算张贴这些红花、黄花、蓝花，你能帮忙数一数它们各有几朵吗？

    生：红花有2朵，黄花有6朵，蓝花有10朵。

    师：我们先来看一看红花和黄花，把它们整理到黑板上。请你仔细观察，其数量之间有什么关系（见图1）？

    生1：红花比黄花少4朵。

    生2：黄花比红花多4朵。

    生3：黄花的数量是红花的3倍。

    生4：黄花的数量比红花多3倍。

    师：真棒！你们不仅会观察，还善于思考。比较两个数量，除了谁比谁多、谁比谁少这种相差关系之外，还可以用倍数关系来表示。这节课我们一起来研究这种关系——“倍的认识”。（板书课题）

    师：刚才一位同学说，黄花的数量比红花多3倍，这句话对不对呢？我们在以后的学习中再讨论。先来看，黄花的数量是红花的3倍是什么意思？

    教学诊断：出现“黄花的数量比红花多3倍”时，教师没有指出学生的错误，只是说我们以后再讨论，其实这个“多3倍”的问题还遗留在学生脑中，学生没有真正理解倍的含义，导致学生在后面的学习中会出现0倍的问题。因此，教师应在课堂上及时解决这个问题。

    当学生说出倍的关系时，教师可以安排其他学生分享自己的想法，辨析问题。

    师：这两句话中都有3倍，它们都对吗？

    生1：黄花的数量是红花的3倍，对的。黄花的数量比红花多3倍，错。

    师：为什么？

    生2：应该是黄花的数量比红花多2倍。

    师：为什么黄花的数量比红花多2倍？

    生2：因为多4朵，就是多2倍。

    师：你观察到了黄花比红花多的部分，多2倍。如果把黄花和红花同样多的部分也算上，黄花的数量是红花的几倍？

    生：3倍。

    师：你能想办法让别人一眼就看出黄花的数量是红花的3倍吗？

    传统教学模式中，教师不喜欢学生出错，当学生出现错误，教师就会用“在以后的学习中再讨论”搪塞过去。这是因为教师捕捉不到错误资源的价值，不知何时解决学生的问题。面对课堂教学中生成的错误资源，教师需要拥有一双智慧的眼睛，将这些错误变为宝贵的教学资源，巧妙地利用，让学生不断发现、思考、探究，将“错点”转化成“亮点”。这样学生的思维能力就在“出现错误”“发现错误”和“改正错误”的深度学习过程中形成，学生对所学知识的理解也会更加深刻，从而提升学生的思维能力。

    学生没有学过倍的概念，出现“黄花的数量比红花多3倍”这个错误是学生对知识的猜测。这时教师不要急于评价，而应巧妙地利用这一错误资源进行引导：“这两句话中都有3倍，它们都对吗？”在教师的引导下学生对猜测进行思考，发现错误。此时教师引导学生进一步思考原因，让学生体会两个关系的比较量不同，一个是黄花的数量，另一个是黄花比红花多的部分，多的4朵是2个2朵，所以是2倍。这样学生体会到了“倍比”是“1份”与“多份”的对应关系，有“几份”就是“几倍”。通过自己纠正错误，学生会整体感受知识自然发生、发展的过程，水到渠成地认识倍，构建“倍”的模型。

    二、争辩错误，让“倍”的概念越辩越明

    【教学片段2】

    师：老师想学魔术师变走一些花朵，变！发生了什么变化？

    生：减少了2朵黄花。

    师：这时黄花的数量是红花的几倍呢？为什么？

    生：把红花看成一份，黄花有这样的2份，黄花的数量是红花的2倍。

    师：如果我再变走2朵黄花，这时，黄花的数量是红花的几倍？

    生1：黄花和红花同样多，所以是0倍。

    生2：0倍不对，刚才黄花4朵时，是2倍;黄花2朵时，怎么一下子变成0倍了？

    师：对啊！黄花是4朵时，是2倍;黄花2朵时，应该是1倍。因此两个数量相等时，它们之间就是1倍的关系。

    教学诊断：第三位学生说完，教师对他的观点进行分析，肯定了1倍的关系，便结束了。其实讨论后坚持是0倍的学生感到不服气，还认为是0倍。这样的讨论不够深入，没有让学生真正理解自己的错误。教师如果让学生进行小组讨论，让所有学生参与辨析，倍的概念会越辩越清晰，越辩越深刻。

    两名学生说完，感觉说0倍、1倍的学生都很有道理，这时教师让学生以四人为小组展开讨论，学生可能还会有新的观点。

    生3：2÷2=1，所以黄花的数量是红花的1倍。

    生4：用圈一圈的方法把2朵红花看成1份，黄花有这样的1份，就说黄花的数量是红花的1倍。

    师：原来1倍就是1份，黄花有红花这样的1份，所以黄花的数量是红花的1倍。这里也可以说红花的数量是黄花的1倍。

    学生会说出0倍，是从比较多少的方面去理解的，认为多出来的部分才是“倍”。这暴露了学生概念建构不到位的问题。虽然教师让多名学生发表自己的见解，但两种不同意见似乎都很有道理，双方均不认同对方的观点。这时教师应给学生多一点儿思考的时间，多一点辩论的时间，这样学生会多一点儿探索成功的喜悦。在四人小组中讨论，每位学生都能发表意见，再次辩论。学生会从争辩中找到错误原因，掌握纠错方法，从而获得真知，深刻地理解概念。

    三、变式防错，让“倍”的知识得到拓展

    在教学的巩固练习中，教师安排了两道估一估的练习：

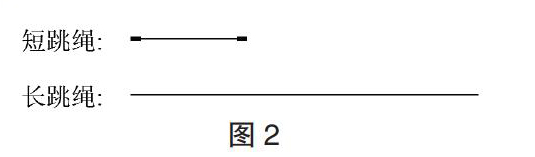
    （1）如图2所示，估一估，长跳绳的长度是短跳绳的（ ）倍。

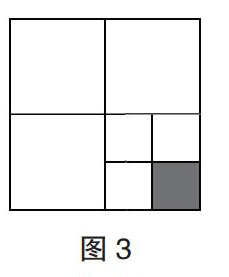
    （2）如图3所示，大正方形的面积是小正方形的（ ）倍。

    学生一般能用画一画、分一分的方法做出这两题，这对学生来说没有挑战性。教师可以设计一道开放性题目，进一步渗透倍的含义。例如，有很多大小相同的圆，你能创造出哪些关于8个圆的倍数关系呢？

    学生会找到很多有关8的倍数： ①8个圆是1个圆的8倍;②8个圆是2个圆的4倍;③8个圆是4个圆的2倍;④16个圆是8个圆的2倍;⑤24个圆是8个圆的3倍……

    教师抓住其中的“8个圆是2个圆的4倍”和“16个圆是8个圆的2倍”，启发学生思考“这两个关系中的8个圆有什么不同？”这样学生能够直面“8个圆”的身份变化：第一个8个圆作为多份数（比较量），第二个8个圆作为一份数（标准量），体会到一个量既可以做一份数，也可以做多份数。

    四、错中反思，让“倍”的教学促科研

    笔者尝试从“倍”的教学过程入手，聚焦学生的错误，紧紧围绕错误资源的合理利用和转化，展开了实践与思考，并形成小课题，为以后的教学探索出一条路径，从而实现教学研究的自我建模。

    1.借助错误，尝试“错误”教学

    学生出现的错误是他们在学习过程中动态生成的一种“利教研学”资源。教师要善于将学生的错误资源作为教学活动的重要内容，引导学生对错误进行分析评价，使学生在纠错、改错中加深对知识的理解，提升其思维品质。

    2.整合错误，设立“错题”超市

    学生在课外学习中也会出现各种错误，这时，教师可以把出错率比较高的题目记录下来，改编并整合出类似的题目，建立班级的“错题超市”，以“菜单”形式供学生随时查阅。学生从“错题超市”中自主选择相应的题目进行巩固，提升自我管理能力和数学学习能力。

    3.分享错误，规避“错误”重现

    在复习阶段，教师可以在“错题超市”选取易错的或有代表性的错题，为学生搭建错题分享平台，组织学生探究错误的原因，避免类似错误再次出现，使学生不断提升自己的解题与辨识错误的能力，拓展思考的广度与深度。

    结 语

    综上所述，教师应抓住学生的认知错误，建构正确的知识体系，提高课堂教学效果;組织学生争辩知识难点，帮助学生理解知识本质;设计拓展练习，延伸知识深度，为学生后续学习做好铺垫;让学生在错题中练，在错题中改。这样，“错误”成了教学中一道亮丽的风景，只要我们注意它的存在，欣赏它的美妙，研究它的根源，从错误中反思教学，就会让教学“倍”感轻松！

    [参考文献]

    余长艳.找原型，抓本质，促发展——观杨迪老师“倍的认识”一课有感[J].小学数学教育，2018（Z1）：139-141.

    作者简介：张滨燕（1986.10—），女，浙江舟山人，二级教师。