动中求静，静中求解

2023.06.15

邹丽虹

[摘? 要] 动点问题一直以来都被中学生视为“拦路虎”，无论是在日常学习中，还是中考时，动点问题都是让学生头痛的知识点. 文章以动点问题的特点为切入点，结合实践探索如何于动中求静，静中求解，帮助中学生突破动点问题的重点与难点.

[关键词] 初中数学;动点问题

动点问题为什么常常让中学生谈之色变？首先在于它在中考中的“出镜率”相当高;其次在于它具有较强的综合性，解题方法灵活，题型变化多端，对学生数学知识运用能力是一个很大的考验，学生们常常因为各种失误而导致解题失败.

动点问题主要考查学生的直觉能力，以及能够从诸多变化中准确找到数学实质的洞察力. 动点问题可以让学生们在猜想、归纳和探究中实现数学思维能力的提升. 但不可否认的是，很多学生也会在动点问题上遇到无法跨越的障碍和瓶颈. 笔者通过多年教学实践，了解到学生面对动点问题无法进行准确解答的主要原因在于，他们不会“动中求静”，不能从题目中找到准确的关系式、条件等信息，造成解题困扰. 我们经常用“箩筐”来形容动点问题，因为任何知识都可以装在里面，结合几何内容就会变成几何动点问题，结合二次函数就会成为函数动点问题. 在这些问题中以函数动点问题最为难解，因此本文结合教学实例，重点对函数动点问题进行了详解，以期让中学生在面对动点问题时，学会如何于动中求静，静中求解.

“一次函数”动点问题

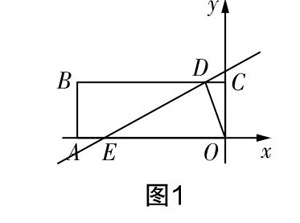
例题设计：如图1所示，四边形OABC为矩形，其中点A坐标是（-3，0），点C坐标是（0，1），线段BC上有一与端点B和C均不重合的动点D，过动点D作直线y=+b与折线OAB相交于点E.

[图1]

（1）如果△ODE面积是S，列出S和b的函数关系式;

（2）当点E在线段OA上，且tan∠DEC=，如果矩形OABC关于直线DE的对称图形是OABC，请大家思考两个图形重叠部分面积会不会发生变化，如果没有发生变化那么重叠部分面积是多少？如果发生变化，讲一讲发生变化的原因.

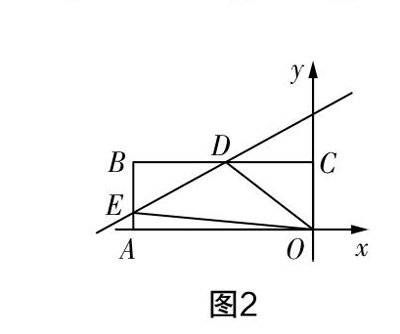
该类题型是關于动态图形面积变化的动点问题，解这类题的关键在于要先看一看对“面积”变化起决定性作用的几个量是不是发生了变化. 这类动点问题难度相对较大，区分度比较明显，对于学生数学思维能力的锻炼和提升十分有益. 而面对这类动点问题，要教会学生们先对题目进行分析：首先，如果想将△ODE的面积表示出来，那么应该从两个方面进行讨论，一方面点E如果在边OA上，只要将△ODE底边OE的长与对应的高，即E点的横坐标和D点的纵坐标求出，再代入三角形面积公式就可以了;另一方面，点E如果在边AB上，那么用长方形OABC面积直接减去△BDE、△OCD和△OAE三个三角形的面积就会得到△ODE面积. 接下来对“重叠部分”进行分析，可以确定的是这部分是平行四边形，这个图形不变的是上下边上的高，所以对重叠部分面积会不会发生改变起决定因素的是边OA上重叠部分的线段长度有没有发生改变. 分析至此，学生们再回过头解题，解题过程就会自然流畅.

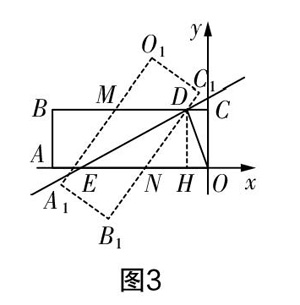
解：（1）从题中可知四边形OABC为矩形，点A的坐标是（-3，0），点C的坐标是（0，1），所以点B的坐标是（-3，1）. 如果直线经过点A，那么b=，如果经过点B，b=，如果经过点C，b=1. 那么，当折线OAB与直线交点在OA边时，1

-b+×3

b-]=b-b2. 所以当1

[图2]

（2）如图3所示，假如CB和OA相交于M点，OA与CB相交于N点，那么说明矩形OABC和矩形OABC两个图形重叠部分面积就是DNEM这个四边形的面积，从题中可知DM与NE平行，DN和ME平行，所以可以判定四边形DNEM是平行四边形. 结合轴对称知识就能够得出∠MED和∠NED相等，又因为∠MDE与∠NED相等，所以∠MED与∠MDE相等，所以MD和ME相等，故DNEM这个平行四边形是菱形. 过D点作DH垂直于OA，H点为垂足. 根据题意可知=，DH=1，所以HE=2. 假设a是菱形DNEM的边长，那么在Rt△DHN里，通过勾股定理可以得出a2=（2-a）2+12，所以a=，S=NE·DH=. 故两个矩形OABC和OABC重叠部分面积不会有变化，面积一直是.

[图3]

“反比例函数”动点问题

例题设计：如图4所示，一次函数y=kx+b的图像经过两点A，B，坐标分别是（0，-2）和（1，0），它和反比例函数y=的图像于第一象限内相交于M点，如果△OBM面积是2.

（1）列出反比例函数和一次函数表达式;

（2）P点是否存在于x轴上，且能够使AM与MP垂直？如果存在请求出P点坐标，如果不存在请说明原因.

[?图4]

该例题主要是对一次函数和反比例函数交点问题的考查，其中涉及求解析式所用的“待定系数法”、锐角三角函数定义等知识点，只要让学生对这些知识进行巩固并熟练掌握，解答这类动点问题就会水到渠成. 因此在引导学生进行分析时，对于问题（1）可以让他们先根据题中所列出的已知条件，即一次函数图像经过两点坐标中可以得出与k，b相关的方程组，然后可以进一步得到一次函数的解析式，再设点M的坐标为（m，n），作垂直于x轴的MD，从“△OBM面积是2”的已知条件中将n值求出，再将M点坐标代入“y=2x-2”中将m值求出，再由M点在双曲线y=上就能够将k的值求出，最后将反比例函数解析式求出. 这时再来分析问题（2）就变得简单了：过M点作与AM垂直并与x轴相交于点P的MP，从MD与BP垂直的条件中可得出∠ABO，∠MBD，∠PMD三个角相等，根据锐角三角函数定义求出OP的值，得到结论即可.

解：（1）因为y=kx+b经过坐标分别为（0，-2）和（1，0）的A，B两点，所以b=-2，

k+b=0，解得b=-2，

k=2，因此一次函数表达式为y=2x-2. 假设过M点（m，n）作垂直于x轴的MD，交点为D点. 因为△OBM的面积是2，所以OB·MD=2，n=2，n=4. 所以将M（m，4）代入函数表达式y=2x-2中就会得到4=2m-2. 所以m=3. 因为M（3，4）在y=双曲线的图像上，所以4=. 故k=12. 因此反比例函数的表达式是y=.

（2）如图5，过点M（3，4）作垂直于AM的MP，并与x轴相交于P点，因为MD与BP垂直，所以得出∠ABO=∠MBD=∠PMD，所以tan∠ABO=tan∠MBD=tan∠PMD===2，所以在Rt△PDM中，=2，由此得出PD=2MD=8，OP=OD+PD=11，点P在x轴上，PM与AM垂直，故P点坐标是（11，0）.

[图5]

从教学实践中笔者得到这样的体会，如何帮助中学生克服对动点问题的恐惧，首先要做好学生的心理建设. 其实动点问题中包含着学习和生活的很多哲理，如通过一个数轴示意图就可以引申到人生维度上，单维度上比长度，双维度上比面积，三个维度就比体积. 而在现实生活中如果想做好一件事，就要从多个维度来思考，也许在某个维度上你不存在优势，但如果每个维度都可以提升一点点，那么综合起来的实力也会击败他人. 从这个切入点先给学生们进行心理引导，帮助他们建立起学习的信心. 然后再通过有效的问题分析帮助学生找准解题思路，熟练解题方法，他们就会明白应如何于动中求静，于静中求解. 一旦掌握了这个方法，无论是动点问题还是其他数学问题，都能轻松应对.