高中地理教师资格考试笔试试题与考纲的一致性研究
刘学梅 张雪雯 陈燕


[摘 要]国家教师资格考试的实施对培养合格中小学教师具有深远的意义。《地理学科知识与教学能力》(高级中学)试题与考试大纲的一致性体现了该科目考试命题的有效性,也影响着考生的考试结果。采用SEC模式分析发现,2014-2018年的10套试题和考试大纲具有显著的一致性,且试题与考纲的“水平要求”维度的一致性要低于“内容主题”维度。原因在于试题中“记忆”“理解”“评价”“技能”内容的比例低于考纲要求,而“应用”“分析”内容的比例高于考纲要求,“创造”内容的比例与考纲要求基本一致。建议完善考纲,加强考纲的可操作性、基础性、科学性与时代性;基于考纲进行命题以进一步提高质量;考生备考应兼顾考纲与真题。
[关键词]高中地理;教师资格考试;考试大纲;SEC模式;一致性
[中图分类号] ??G451 [文献标识码] A [文章编号]1005-5843(2019)05-0097-07
[DOI]10.13980/j.cnki.xdjykx.2019.05.019
自2011年下半年起,国家教师资格考试制度开始在湖北、浙江两个省份进行试点。截止2019年1月,除了西藏、内蒙古、新疆等省(市、区)外,全国有28个省(市、区)参加了改革试点。国家教师资格考试分为笔试和面试两部分,笔试包括“综合素质”“教育知识与能力”“学科知识与教学能力”等3个科目。前两个科目是所有考生必考科目,科目三则针对不同学科。依据《地理学科知识与教学能力(高级中学)》考试大纲(下文简称“考纲”)的规定,科目三包括“地理学科知识与运用”“教学知识与运用”“教学设计”3个模块。按照考试目标,“考试内容模块与要求”对每个模块提出了具体要求,并且运用“了解”“掌握”“理解”“运用”等不同词语对考生应掌握的知识点及其程度进行了区分。总之,考试大纲从不同方面对考生提出了具体要求。但是,国家教师资格考试是否很好地发挥了选拔合格教师的功能?《地理学科知识与教学能力(高级中学)》试题(下文简称“试题”)的考查内容与考查水平是否严格执行了考纲的要求?二者的一致性程度如何?对这些问题的反思有利于提高国家地理教师资格考试的命题质量,也有利于考生进一步进行有效的学习与备考。
一、基于SEC模式的一致性分析
一致性是指分析与判断两种及两种以上要素间的相互吻合程度[1]。笔者在本文中主要研究2014-2018年中的试题与考纲的吻合程度。当前较为流行的一致性分析工具主要包括Webb模式、Achieve分析模式和SEC模式,笔者选择了SEC模式。该模式由波特(A. Porter)等人于2001年创建,主要用于课堂教学与学业评价的一致性分析。它的优势是提供了详细的计算公式与临界参考水平。其基本步骤是:第一,构建二维矩阵。对研究对象进行“内容主题”与“水平要求”两个维度的划分,并在此基础上构建由“内容主题”与“水平要求”组成的二维矩阵。第二,编码与统计。在二维矩阵的框架下对研究对象进行编码与统计,得到相关的二维矩阵。第三,计算与分析。依据公式P=1-[SX(]n[]i=1Ai-Bi[]2[SX)](Ai、Bi分别表示两个相同大小矩阵中对应单元格中的比率数据)对二维矩阵产生的比率值进行计算,得到一致性系数P。P的范围为0到1,P值越大则一致性程度越高。当P=0时,二者完全不一致;当P=1时,二者完全一致。
(一)一致性分析框架的确定
依据SEC 一致性分析范式和考试大纲,内容主题分为“地理学科知识与运用”“教学知识与运用”“教学设计”三个模块。依据布鲁姆教育目标分类法,笔者将水平要求划分为认知水平和技能水平。认知水平分为“记忆”“理解”“应用”“分析”“评价”“创造”六个层次的一致性分析框架。
(二)考纲的编码分析
首先,对考纲进行深度剖析并对水平要求进行分类标记。水平要求的确定主要依据为考试大纲中的“考试内容模块与要求”,结合考试目标以及具体情境和认知过程,最后得到的分析结果(见表1)。通过对考纲中的编码数量数据进行处理,得出不同水平要求的数量(见表2)。
其次,对考纲的编码结果进行标准化处理。根据考纲要求,试题总分为150,“地理科学知识与运用”约占66分,“教学知识与运用”约占31分,“教学设计”约占53分。对内容主题中的各个水平要求进行分值计算,得到考试大纲的编码比率(如表3所示)。
(三)试题的编码分析
首先确定每道试题对应的内容主题,其次确定该道试题对应的二级内容主题,再判断该考题对应“水平要求”中的具体水平,最后形成3×7的二维矩阵,得出最终结果。如对2015年上半年的试题进行编码,得到表4所示的结果。重复此步骤,完成对其他9套试题的编码。
二、基于SEC模式的一致性分析结果
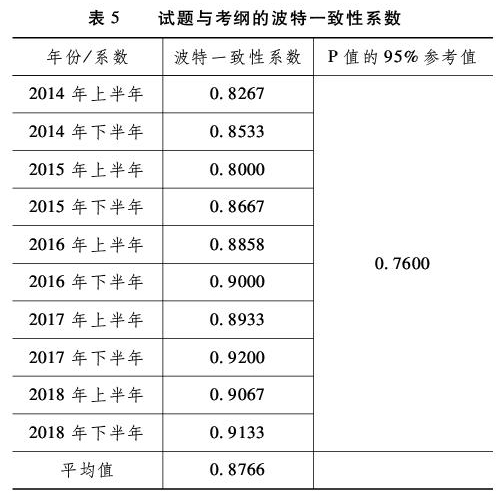
对5年中的10套试题进行编码分析,分别得到一个波特值。根据学者加文(Gavin)的思路,使用Matlab中Unidrnd函数,将若干个主题内容标准随机赋值到相应的矩阵中,同样将试卷内容要素随机赋值到另一矩阵中,经专业化处理后就可得到一个P值,把此操作进行20 000次重复,得到P值的95%数据参考值。只有计算结果大于或等于这个值时,才能说明二者具有统计学范畴上的显著一致性[2]。在对试题进行编码统计分析后,根据SEC模式分析法中的公式进行计算得到如表5所示的一致性系数。
(一)总体分析
总体上看,2014-2018年的试题及与考纲的一致性系数都高于0.76(如表5所示),说明试题与考纲具有统计学范畴上的显著一致性。另外,近5年的波特一致性系数总体呈增长趋势,试题与考纲的一致性越来越高。此外,通过计算得出历年的波特一致性系数的平均值为0.8766。2014-2015年间的4套试题与考纲的波特一致性系数均低于平均值,2016-2018年间的6套试题与考纲的波特一致性系数均高于平均值。其中,2015上半年波特一致性系数最低,为0.8;2017下半年波特一致性系数最高,为0.92。由表6可知,2015年上半年的试题特别注重对考生“应用”和“分析”水平的考查,所占比重之和约为53.34%。其中,“记忆”“理解”及“创造”水平所占比重都在10%以上;“評价”和“技能”水平涉及较少,“技能”水平仅占4%,“评价”水平则为0。由表7可知,2017年下半年的试题极其强调考生的“分析”和“创造”水平,所占比重之和约为41.34%。其中,“记忆”“理解”及“应用”水平所占比重都在10%以上;“评价”和“技能”水平占比较低,两者之和不超过10%,与考纲要求基本一致。

