一种基于非下采样Contourlet变换的去噪算法

    朱丽

    

    

    摘要：文章提出了一种新的去噪算法，算法是基于非下采样Contourlet变换（NSCT）的自适应阈值。首先需要对含噪图像进行非下采样Contourlet变换，然后得到各个尺度各个方向子带的系数。为了克服软、硬阈值函数的缺点，提出了一种自适应的新阈值函数。仿真实验表明，文章方法在峰值信噪比（PSNR）、信噪比（SNR）、均方误差（MSE）与视觉效果上均优于其他去噪算法。

    关键词：阈值去噪；非下采样；Contourlet变换

    1 Contourlet变换算法

    Contourlet变换（cT）的思想是为了实现对图像信号的稀疏分离，而使用类似于线段的基函数去逼近原始图像。Contourlet变换采用塔型方向滤波器组（PDFB），也就是“双重滤波器组”的结构，它由拉普拉斯金字塔滤波器（LP）和方向滤波器组（DFB）组成。

    LP分解是一种多尺度的分析方法，LP分解的缺点是由于在高频部分没有下采样，暗含了过采样，因此对图像的冗余度趋向于4/3。

    方向滤波器（DFB）的核心是如何将方向频率进行划分，新的DFB通过简单的分解树规则，不仅最后归结为多通道形式，还大大简化了原来的树状分解规则。

    方向滤波器组（DFB）虽然能够获取图像中具有方向性的高频信息，但对低频信息的处理相当差。

    Contourlet变换（CT）具有良好的方向选择性及各向异性，可以在不同尺度不同方向的频率子带中将图像中的边缘信息准确的表示出来。但是CT过程中采用的下采样操作不具有平移不变性，在去噪时会产生伪吉布斯现象，且在子带存在频谱混叠现象，在CT的多方向选择性中产生了一定程度上的消弱。为了克服这一缺点提出了具有平移不变性的非下采样Contourlet变换。

    非下采样Contourlet变换就是将金字塔分解和方向滤波器结合起来，其实现的过程如下。

    （1）通过LP变换，图像信号被分解为高频分量和低频分量两部分，奇异点的捕捉可以利用拉普拉斯金字塔滤波器对图像进行多尺度分解。

    （2）为了使同一尺度同一方向上的奇异点合并成一个系数，需要利用方向滤波器组将各尺度上的细节子带进行多方向分解。

    2 非下采样Contourlet自适应阈值去噪

    2.1 自适应阈值的选取

    图像去噪中的一种常见的去噪方法是阈值去噪。阈值去噪过程中的一个重要因素是选取阈值函数，Contourlet系数在不同的阈值函数中有不同的处理方式。常用的阈值函数主要有硬阈值函数和软阈值函数。

    通过函数连续性可以得出，硬阈值函数可以得到较好的去噪效果，但会使含有丰富边缘的图像产生“人为”的噪声点，从而使处理后的图像出现视觉失真如伪吉布斯效应等现象。而软阈值函数处理后的图像平滑，同时也较好的解决了伪吉布斯效应，但会导致处理后图像边缘的模糊。于是针对软、硬阈值函数存在的问题，提出一种具有可调节自适应性的新阈值函数。新阈值函数可以根据各个图像分解后不同的尺度及方向自适应的进行参量调节。

    2.2 算法技术实现

    Contourlet变换和小波变换类似，因为缺乏平移不变性，图像去噪后容易产生伪吉布斯现象，本节采用非下采样Contourlet变换图像去噪方法，算法实现过程为：

    （1）首先对含噪图像进行循环平移，得到平移子图像。

    （2）对每一个平移子图像进行Contourlet变换，将图像分解为各个尺度方向细节子带和低频分量。

    （3）用本节提出的阈值公式，求出各个尺度各个方向上的阈值。

    （4）为得到去噪结果，对去噪后的Contourlet系数进行了逆变换。

    （5）对每个去噪结果分别进行逆循环平移，得到去噪后的子图像，对所有去噪后的子图像进行线性平均，得到去嗓后的图像。

    3 仿真实验结果及分析

    为了验证在图像去噪上这种自适应阈值的正确性和有效性，本节选择高清摄像机下某型雷达侦察装备仿真试验中录像视频图像，设定其高斯白噪声的叠加均值为零进行实验。

    高斯白噪声的方差分别为2.00，2.25，2.50，2.75，3.00。实验中我们将本节所提出的去噪方法与小波阈值去噪和Contourlet阈值去噪进行了比较。在实验中，我们对去噪后图像的客观质量进行了衡量，对峰值信噪比（PSNR）、信噪比（sNR）、和均方误差（MSE）进行对比。

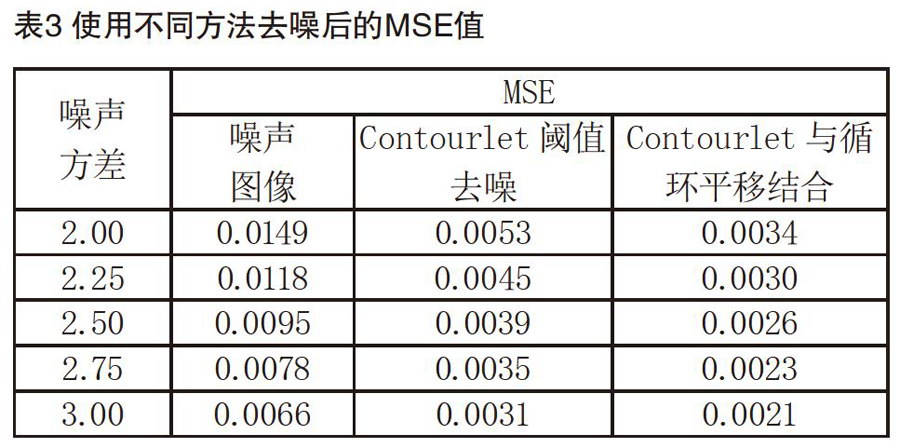
    实验结果如表1、表2和表3所示。

    通过分析表1、表2中的数据，可以看出Contourlet阈值去噪方法比Contourlet与循环平移结合的去噪算法的PSNR值的PSNR值高，但随着噪声方差的增加PSNR值提高的越少。同样，Contourlet阈值去噪方法比Contourlet与循环平移结合的去噪算法的sNR值高，但随着噪声方差的增加sNR值提高的越少。

    通过分析表3中的数据，可以看出Contourlet阈值去噪方法比Contourlet与循环平移结合的去噪算法的MSE值低，但随着噪声方差的增加MSE值降低的越少。

    4 结语

    根据在不同尺度和方向上Contourlet系数的特性，选取一种自适应阈值，利用这种阈值可以准确的抓住系数在各个尺度和各个方向上存在的差异，在很好的保留图像细节信息的同时可以有效的去除噪声，使图像的视觉效果更好。