蝙蝠算法优化近红外光谱校正模型测定柴油黏度

    胡振 陈素彬 张晓琪 唐天国 杨华

    

    

    

    摘 ?????要：为了提高近红外光谱定量分析的精度和效率，提出以改进二进制蝙蝠算法同步优化参数和特征波长的LS-SVM模型。首先将动态速度权重和Cauchy随机扰动融入蝙蝠算法，并用V-shaped函数将其离散化，得到WCBBA算法;然后以RMSECV为适应度函数，用WCBBA算法对LS-SVM模型的参数和特征波长进行同步优化;最后根据优化结果建立近红外光谱定量校正模型，并用于180个柴油样本的运动黏度测定。结果表明，该模型的各项性能指标优异，能够用于实际检测工作。

    关 ?键 ?词：蝙蝠算法;近红外光谱;定量模型;参数优化;特征波长

    中图分类号：TQ016;O657.33 ????文献标识码： A ??文章编号： 1671-0460（2019）03-0647-05

    Abstract： In order to improve the accuracy and efficiency of the quantitative analysis of the near infrared spectrum， a LS-SVM model was proposed to improve the binary bat algorithm's synchronization optimization parameters and characteristic wavelengths. First， the dynamic velocity weight and the Cauchy random disturbance were integrated into the bat algorithm， and the V-shaped function was used to discretize it， the WCBBA algorithm was obtained. Then the RMSECV was used as the fitness function and the WCBBA algorithm was used to synchronize the parameters and characteristic wavelengths of the LS-SVM model. Finally， a quantitative correction model of near infrared spectroscopy was established based on the optimization results， and 180 diesel samples were used to measure the kinematic viscosity. The results show that the model has excellent performance and can be used for practical testing.

    Key words： Bat algorithm; NIRS; Quantitative model; Parameter optimization; Characteristic wavelength

    近红外光谱（Near Infrared Spectroscopy，NIRS）分析是目前主流的仪器分析技术之一，具有无损、快速、重复性好、污染少、成本低等优势，能对各种气、液、固态样品进行定量和定性分析，可同时满足批量检测的准确度和在线监测的快速性要求，因而广泛应用于农业、食品、医药、化工、材料等领域。但是，近红外光谱定量分析是一种间接定量技术，需先以化学方法测定样品的待测属性值，并在相应的波长范围采集光谱数据系列;然后将样品按特定的方法划分为校正集和验证集，建立一个该类样品的近红外光谱与其待测属性值之间的校正模型，并检验其有效性;最后将该模型应用于未知样品，即可由其光谱数据计算待测属性值。

    由于各类样品组分众多、结构复杂，而近红外光谱重叠严重、信噪比低，加之仪器响应特性和人为操作误差等不利因素影响，使待测属性与光谱数据之间并非总是简单的线性相关，而是更多表现为复杂的非线性关系，因此建模时需运用化学计量学方法和软件技术，采取先进的建模方法并对模型进行有效的优化，才能得到一个准确、高效、稳健的近红外光谱定量校正模型。本文以最小二乘支持向量机（Least Squares Support Vector Machine，LS-SVM）为建模方法，主要探讨利用改进的蝙蝠算法（Bat Algorithm，BA）优化近红外光谱定量校正模型的参数和波长等问题，并将该优化模型用于柴油的运动黏度测定。

    1 ?近红外光谱定量校正模型的建立

    1.1 ?近紅外光谱的特性及建模要求

    近红外光谱是由分子的非谐振动而从基态向高能级跃迁时产生的，表现为含氢基团X-H（X=C、O、N、S等）在780～2 526 nm波长谱区振动的倍频和合频吸收，能反映大多数有机化合物和混合物的组成、结构与状态信息。各种基团（或处于不同化学环境的同一基团）在近红外谱区具有特定的吸收波长与强度，其吸收（反射）程度与相应物质成分含量之间的相关性符合Beer-Lambert定律，故可为之建立一个近红外光谱定量校正模型，即能由物质的近红外光谱强度预测相应成分的含量。

    近红外谱区吸收带较宽、吸收强度较弱，且倍频、合频谱带严重重叠，致使原始谱图中存在大量共线性变量和冗余信息;而光谱仪的温湿度响应特性、样品粒度（密度）不均、操作失当等因素也难以避免，导致近红外谱图通常含有随机噪声、基线漂移、杂散光和样品背景等非目标信息，故其信噪比较低。因此，在建立近红外光谱校正模型时，应以适当方法进行数据预处理、异常样本检测和样本集划分，尽量消除其中的干扰信息，增强样本的代表性，以提高光谱信息与待测属性之间的相关性;同时采用有效算法从原始光谱中优选特征波长变量，摒弃与待测属性无关的信息，并对模型参数进行优化，以提高其精度、速度和泛化性能。

    1.2 ?LS-SVM校正模型的建立

    建立近红外光谱校正模型的方法可分为线性回归和非线性回归两类。前者包括多元线性回归（Multivariate Linear Regression，MLR）、主成分回归（Principal Component Regression，PCR）和偏最小二乘（Partial Least Squares Regression，PLSR）等;后者以BP神经网络（Back Propagation Neural Network，BPNN）、LS-SVM和极限学习机（Extreme Learning Machine，ELM）为代表。两相比较，线性方法简便易行、应用广泛，但当物质的待测属性与光谱数据之间的线性相关度较差时，不适合建立线性回归模型[1];非线性方法适应性强、稳健性好，但通常需要对模型参数进行优化。

    LS-SVM支持线性和非线性建模，其训练为求解线性方程组，预测则是计算各建模样本与待测样本之间的核函数，计算量仅取决于校正集的样本数目，而与光谱维数无关。LS-SVM模型比一般线性模型更稳健性，且避免了人工神经网络普遍存在的训练速度慢、易早熟、过拟合和泛化性差等缺陷。在分析检测工作中，通常利用LS-SVMlab工具箱函数，以MATLAB编程来实现LS-SVM校正模型。

    2 ?蝙蝠算法及其改进

    2.1 ?基本蝙蝠算法及其缺陷

    蝙蝠算法[2]是Xin-She Yang基于蝙蝠的回声定位特性提出的一种群体智能搜索算法，其求解准确性和有效性优于常用经典算法，且模型简单、效率高，具有潜在并行性和分布式特性。其基本过程为：

    对于非线性最小值目标函数，设蝙蝠数量为n，在d维搜索空间中，个体i∈（1，2，...，n）在t时刻的速度和位置分别为vit =（vi1t，vi2t，...，vidt）、xit =（xi1t，xi2t，...，xidt），则在（t+1）时刻其速度和位置按下列公式更新：

    显然，基本蝙蝠算法的优化能力主要源于个体间的相互作用，而没有提供能够保持种群多样性的变异机制，故易发生早熟收敛而影响寻优精度，并因强化局部搜索而导致了后期进化变慢[3]。

    2.2 ?引入动态权重与Cauchy扰动的蝙蝠算法

    针对蝙蝠算法的缺陷，我们引入动态速度权重因子和Cauchy分布随机数扰动，以保持种群的多样性，增强其全局搜索能力，同时加快收敛速度。

    2.2.1 ?引入动态速度权重因子

    蝙蝠算法与粒子群优化算法（Particle Swarm Optimization，PSO）的数学模型和运行机制非常相似，并可通过参数设置转换为后者，故可借鉴PSO算法引入惯性权重，即为BA的速度变量增加一个权重因子w，并令其在预设区间[wl，wu]动态递减，再将式（2）替换为式（7）：

    2.2.2 ?施加Cauchy分布随机数扰动

    在基本BA中，当rand

    Cauchy分布的概率特性是两翼较长，容易产生远离原点的随机数。因此，对蝙蝠位置施加Cauchy分布随机数扰动，有利于保持群体的多样性，降低陷入局部最优的概率，从而有效提高算法的全局搜索性能。对蝙蝠位置xi的扰动按式（8）进行：

    2.3 ?二进制蝙蝠算法及其改进

    为解决组合优化问题，需对蝙蝠算法做离散化处理，将其搜索空间由连续的实数空间映射到离散的二进制空间[4]，即为二进制蝙蝠算法（Binary Bat Algorithm，BBA）[5]：蝙蝠的各维位置都限定为二进制0或1，但其速度大小则不限制[6]，故可用传递函数将速度转换为概率值来确定个体的位置。若以V-shaped函数[7]进行离散化，则相应公式如下：

    显然，BBA主要以式（9）-（10）取代了BA的式（3），其余流程则基本一致，因而也继承了后者固有的缺陷。为此，以2.2所述基于动态权重和Cauchy随机扰动的BA为基础，将其进行离散化处理即得相应的改进BBA，可称之为WCBBA。

    3 ?用改进蝙蝠算法优化NIRS定量校正模型

    3.1 ?LS-SVM模型参数的优化

    LS-SVM模型的参数随其核函数而不同。一般情况下，径向基函数（Radial Basis Function，RBF）因其支持向量少、计算简单、支持小样本训练集等优势而被广泛采用，但其正则化参数γ和核宽度σ2会直接影响模型的泛化性能、支持向量数目和预测精度，因此对其进行优化是至关重要的。

    在常用的LS-SVM模型参数优化方法中，单纯形法（Simplex）稳定性较差，结果差异较大;网格搜索法（Grid Search）较复杂、精度偏低，不宜于大样本集;遗传算法（Genetic Algorithm，GA）、PSO算法则易发生早熟收敛而影响模型精度。

    3.2 ?特征波长变量的选择

    原始近红外光谱中含有大量共线性变量和非目标信息，会严重影响模型的性能和效率，故应在建模时选取特征波长变量，摒弃无关信息、降低数据维数、简化模型，提高其精度、速度和稳健性。

    选择特征波长的常用方法包括无信息变量消除（Uninformative Variable Elimination，UVE）、连续投影算法（Successive Projections Algorithm，SPA）、竞争性自适应重加权采样法（Competitive Adaptive Reweighted Sampling，CARS）、间隔偏最小二乘（interval Partial Least Squares，iPLS）及其衍生算法SiPLS/BiPLS/MWPLS等。近年来，GA和PSO等智能算法因其搜索空間的多样性和全局寻优等特性而逐渐用于波长优选，并取得了较好的效果。

    3.3 ?用WCBBA同步优化模型参数和特征波长

    现有研究几乎都以不同方法将模型参数优化与特征波长选择分步进行，但二者在同一个NIRS定量校正模型中是相互影响的[8]，将其置于同一过程进行联合优化才能得到最佳结果。为此，本文针对以LS-SVM方法所建NIRS定量校正模型，运用WCBBA来实现建模参数与特征波长的同步优化。

    3.3.1 ?优化变量编码

    首先考虑NIRS的特征波长选择问题，以蝙蝠的各维位置对应波长变量，若某维取值为1，则相应波长的光谱数据被选中，反之表示未选中[9]。取值为1的各维对应的波长组合即为特征子集;与此同时还需寻求LS-SVM模型（RBF核函数）参数γ和σ2的最优值，以求模型的性能达到最佳。

    在WCBBA中对优化变量进行二进制编码，它由参数γ、σ2和特征集3个部分构成。设Bi为蝙蝠个体i的编码，则可表示为：

    3.3.2 ?适应度函数

    在对NIRS定量校正模型的参数和波长变量寻优过程中，采用留一法交叉验证（Leave-One-Out Cross Validation，LOO-CV）规则进行建模、预测，以常用性能指标之一的交叉验证均方根误差（Root Mean Square Error of Cross Validation，RMSECV）作为适应度函数[10]：

    3.3.3 ?优化和建模流程

    （1） 样本集数据预处理、异常样本检出，并将其按4：1～3：1划分为建模集和预测集。

    （2） 设置WCBBA各参数，初始化蝙蝠群B。

    （3） 从建模集中取1个样本作测试集、其余为训练集，按式（11）将蝙蝠的二进制编码转换为LS-SVM的参数γ、σ2和特征集，进行NIRS校正模型训练和测试。重复本步骤至各样本皆作测试集。

    （4） 以式（12）计算RMSECV，将其作为适应度更新当前最优的个体位置和全局位置。

    （5） 依式（6）、（1）和（7）更新權重因子、脉冲频率和速度，再由式（9）和（10）进行位置更新，并根据条件执行式（8）;按式（5）更新脉冲速率和响度。

    （6） 若达到最大迭代次数，则输出全局最优个体位置;否则重复执行步骤（3）-（5）。

    （7） 由全局最优个体位置解析出参数γ、σ2和特征子集，据此建立NIRS定量校正模型，并应用于预测集进行验证。

    为了区别于普通的LS-SVM建模方法（通常仅做参数优化），将按上述流程设计、实现的LS-SVM模型称为WCBBA-LSSVM模型。

    4 ?以优化NIRS定量校正模型测定柴油的运动黏度

    柴油是发动机的主要燃料之一[11]。黏度是表征柴油使用性能的重要指标，对发动机的供油量、雾化质量及供油系统精密偶件的润滑都有重要影响，国家标准GB 252-2015《普通柴油》和GB 19147-2016《车用柴油》均将运动黏度列为控制指标。测定柴油运动黏度的国标方法为GB 265-88《石油产品运动黏度测定法和动力黏度计算法》，但需用仪器、试剂较多，准备工作与试验步骤繁琐、耗时较长[12]。因此，尝试建立近红外光谱定量校正模型来检测柴油样品的运动黏度。

    4.1 ?样品化学检测、NIRS采集与数据处理

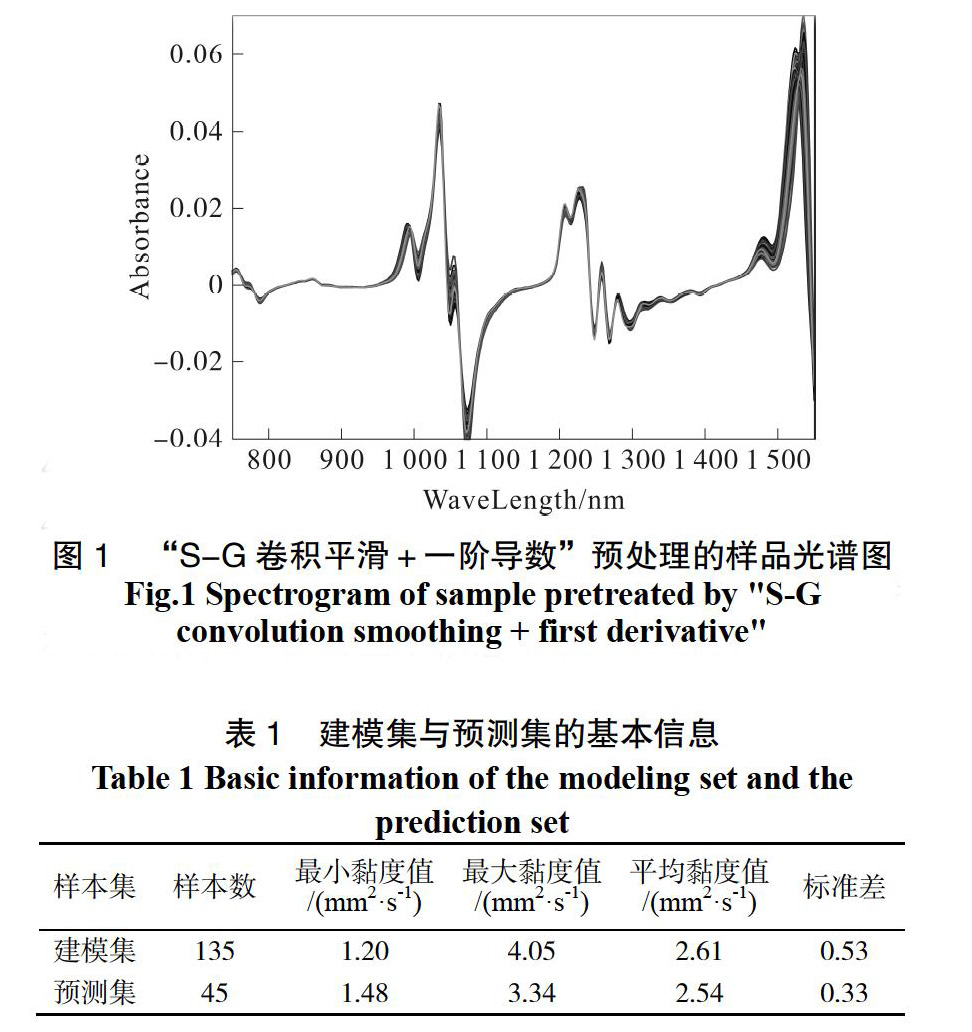
    采集0#柴油样品187个，以国标方法测其同温条件下的运动黏度，并用光谱仪扫描得到各样品在750～1 550 nm波长区间（间隔2 nm）的401个NIRS数据。尝试、对比了多种数据预处理算法，包括中心化（Centering）、归一化（Normalization）、标准正态变量变换（Standard Normal Variable，SNV）、平滑（Smoothing）、导数（Derivative）和多元散射校正（Multiplicative Scatter Correction，MSC）等，以组合方案“S-G卷积平滑+一阶导数”所得结果最佳;再用蒙特卡洛交互验证法（Monte Carlo Cross Validation，MCCV）剔除异常样本后，剩余180组样本数据，相应的预处理光谱如图1所示。

    4.2 ?NIRS定量校正模型建立与验证

    4.2.1 ?样本集划分

    以KS法将180组样品数据按3：1划分为建模集和预测集，二者的基本信息如表1所示。

    4.2.2 ?LS-SVM模型参数和特征波长的同步优化

    根据3.3.3所述的优化建模流程，在MATLAB R2015b环境中，首先编程实现WCBBA优化主程序;然后利用LS-SVMlab 1.8工具箱函数编写适应度函数——柴油样品的NIRS交叉验证模型，返回RMSECV作为WCBBA算法的适应度值。

    算法参数设置：最大迭代次数60，蝙蝠种群规模40;速度权重区间[1.0， 0.5]，脉冲频率范围[0， 2];声波响度A和脉冲速率r的初值分别为0.25、0.1，前者的衰减系数和后者的增强系数均为0.9。以网格搜索法确定LS-SVM模型参数的搜索范围为γ∈[6.638 7e2， 1.979 0e6]、σ2∈[6.334 2e-4， 9.397 4e-2]，并将其二进制编码长度皆设为20位;再加上特征波长集的编码长度401位，最终所得优化变量的二进制编码串为441位。

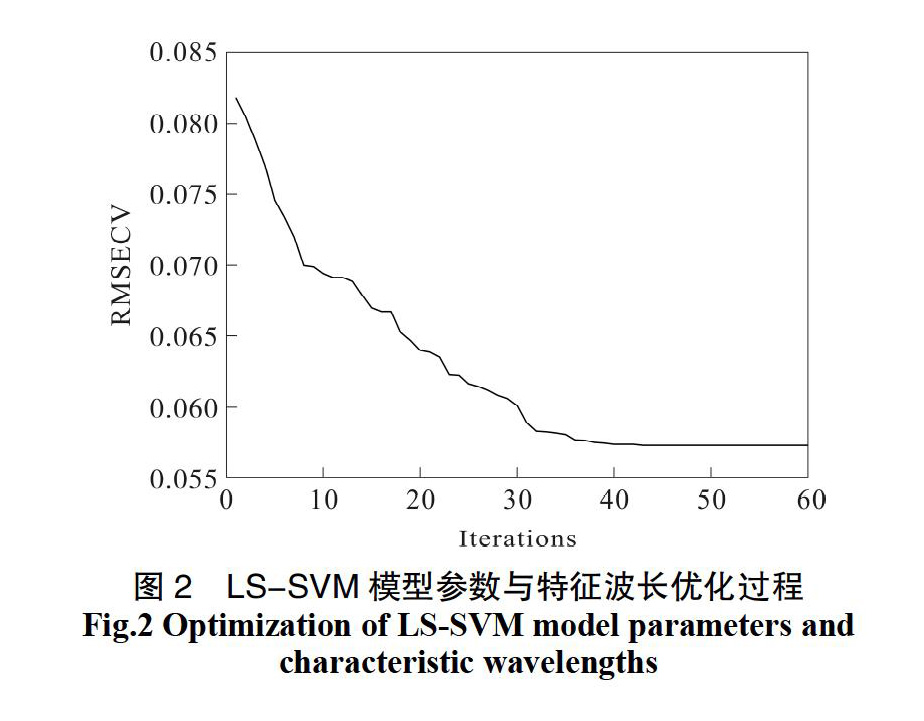
    载入建模集数据运行优化程序，得到模型参数γ= 871 294.759 1、σ2= 0.026 0，同时选出波点数165个。优化过程中RMSECV变化如图2所示。

    4.2.3 ?优化的NIRS模型建立与预测

    用LS-SVMlab 1.8工具箱函数编程建立柴油样品的NIRS定量校正模型，代入优化所得参数γ、σ2和特征波长集，以预测集数据运行、测试之，并通过相关系数Rc2和Rp2、均方根误差RMSEC和RMSEP、相对分析误差RPD评价其性能。

    4.3 ?结果与比较分析

    为了验证WCBBA-LSSVM模型的有效性，同时还用表1的样本集数据建立PLS、CARS-PLS和LS-SVM模型进行测试比较，结果如表2所示。

    由表2的数据可知，四种模型的Rc2>0.96、Rp2>0.89、RMSEC<0.11、RMSEP<0.11、RPD>3，因此均具有较好的性能，能够应用于实际检测工作，相比之下，PLS和CARS-PLS模型的各项性能指标非常接近，其Rc2、Rp2和RPD较小、RMSEC和RMSEP较大，表明其预测精度偏低。而LS-SVM模型的Rc2、Rp2和RPD显著增大、RMSEC和RMSEP明显减小，故其性能大幅领先于前两种模型;在此基础上，WCBBA-LSSVM模型并进一步提高了Rp2和RPD、降低了RMSEP，且Rc2和Rp2、RMSEC和RMSEP这两对指标值相差更少，因此其预测精度、稳健性和泛化性能更佳。

    在四种模型中，CARS-PLS模型的建模波点数最少，故其具有结构精巧、运行高效的优势，但其各项性能指标远不及WCBBA-LSSVM模型，说明其尚有部分特征波长未被选入建模特征集中;WCBBA-LSSVM模型则将建模波点数缩减为全部波长的1/3，且在简化结构、提高速度的同时，显著地改善了模型的性能。

    5 ?结束语

    本文运用改进的二进制蝙蝠算法实现近红外光谱校正模型参数和特征波长的同步优化，构建了一种WCBBA-LSSVM模型，将其应用于180个柴油样品的运动黏度检测，并与常用的PLS、CARS-PLS和LS-SVM模型进行对比。所得Rc2和Rp2分别为0.997 2、0.984 2，RMSEC和RMSEP分别为0.027 6、0.040 7，RPD达到8.06，各项指标皆显著优于PLS、CARS-PLS和LS-SVM模型，表明该模型的预测精度高、外推性好、适应性强，能满足实际检测要求。

    参考文献：

    [1]包鑫. 稳健回归技术及其在光谱分析中的应用[D]. 杭州：浙江大学，2010.

    [2]Yang XS.A new met heuristic bat-inspired algorithm[M]. González JR， Pelta DA， Cruz C， et al. Nature Inspired Cooperative Strategies for Optimization. Berlin Heidelberg： Springer， 2010：65-74.

    [3]張晓琪，胡振，唐天国. 改进蝙蝠算法在模糊层次分析中的应用[J]. 计算机系统应用，2018，27（3）：146-152.

    [4]刘天健. 禁忌搜索的混合蝙蝠算法的研究及应用[D]. 南宁：广西大学，2016.

    [5]Mirjalili S， Mirjalili S M， Yang X S. Binary bat algorithm[J]. Neural Computing and Applications， ?2014，25（3）：663-681.

    [6]李贺，靳庆路，高善波. 基于蝙蝠算法的含分布式电源配电网故障定位[J]. 电气技术，2017，18（1）：34-38.

    [7]Mirjalili S， Lewis A. S-shaped versus V-shaped transfer functions for binary particle swarm optimization[J]. Swarm and Evolutionary Computation，2013，9（1）：1-14.

    [8] 张进，丁胜，李波. 改进的基于粒子群优化的支持向量机特征选择和参数联合优化算法[J]. 计算机应用，2016，36（5）：1330-1335.

    [9]李航，赵海东，申金媛，等. 基于BPSO和SVM的烟叶近红外有用特征光谱选择[J]. 物理实验，2015，35（6）：8-12.

    [10]刘泽蒙，张瑞，张广明，等. 基于离散萤火虫算法的近红外波长优选方法研究[J]. 光谱学与光谱分析，2016，36（12）：3931-3936.

    [11]陈素彬，胡振. 近红外光谱的ELM校正模型测定柴油凝点[J]. 当代化工，2017，46（5）：1010-1013.

    [12] GB 265-88 石油产品运动黏度测定法和动力黏度计算法[S].北京：国家标准局，1988.