动态规划案例教学设计
刘光霆+蔡万铭+沈鑫+向朝参

[摘 要]在运筹学的分支体系中,动态规划因其应用的广泛性而占有十分重要的地位。针对动态规划教学中的难点,可以以最短路问题为引例,以大家耳熟能详的名称对动态规划中的基本概念进行阐释,并对最优性原理、无记忆性与记忆性进行比较系统的阐述,指出最优性原理表现在最短路问题中即是“最短路径的子路径必然是最短的”。最后,还可以以最短路分析动态规划求解时常用的“空间换时间”策略。
[关键词]动态规划;最优性原理;无记忆性;记忆性
[中图分类号] TP399 [文献标识码] A [文章编号] 2095-3437(2016)01-0108-02
在运筹学的分支体系中,动态规划因其应用的广泛性而占有十分重要的地位。但动态规划仅仅是解决某类特殊的多阶段决策问题的一种方法,不具有统一的数学模型和算法步骤[1],而且概念多,因此学生普遍反应“动态规划真的有用但确实难学”。本文以最短路问题为案例,对动态规划相关概念、最优性原理、无记忆性等进行了阐释。
一、案例的选择
可用动态规划求解的问题很多,如最短路、资源分配、生产与存储等,而最短路问题因其空间特征明显,易于划分阶段、易于描述每阶段开始和结束时的状态,以及在每个状态之下做出的决策、每次决策产生的决策指标值等,因此,对初学者而言,最易接受和理解的例子还是最短路问题。本文以最短路问题作为引例,帮助学生们理解和掌握动态规划的相关概念及基本方程、最优性原理等。
二、相关概念的解释
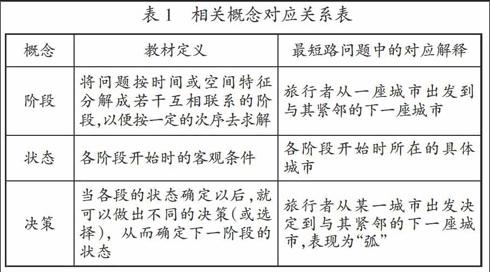
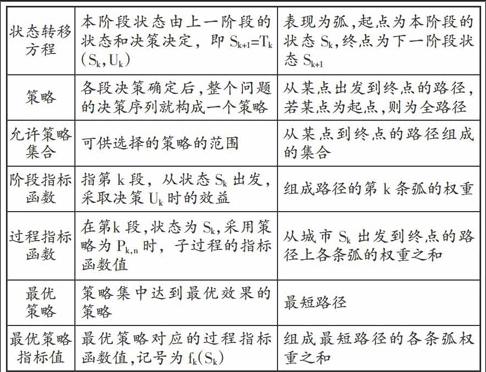
动态规划相关概念繁多,从阶段、状态开始,到过程指标函数,刚接触时,不少学生感到一头雾水,十分茫然。而借助于最短路问题,将动态规划的相关概念与最短路问题中大家耳熟能详的名称相对应,则十分有助于学生对动态规划基本概念的把握。相关概念具体对应关系如表1所示。
从上表可知,动态规划的基本概念在最短路问题中都可找到与之对应的解释,非常有助于学生掌握动态规划问题的实质。
三、最优性原理的解释
教材[1]对最优性原理作了如下表述:无论过去的决策和状态如何,对前面的决策所形成的当前状态而言,余下的决策序列必须构成最优策略,即最优策略的子策略总是最优的。
对最优性原理,部分学生将其理解为:组成最优策略的决策必须是最优的。产生这种误解的原因是将决策与策略相混淆。在动态规划中,决策指的是在某种状态下作出的一种选择,是一种瞬时行为。决策无优劣之分,每一步决策会产生一个决策指标值rk(Sk,Xk),它只是说明本次决策产生的益损值;而策略是由一系列决策所组成,策略是决策的集合,策略有优劣之分,度量策略优劣的数量指标值就是指标函数值fk(Sk)。一般而言,指标函数值是决策指标值的和或积的形式,即
fk(Sk)=opt(rj(Sj,Xj))或fk(Sk)=opt(rj(Sj,Xj))。
因此,单步决策的最优化一般不可能产生全策略的最优化,而子策略的最优化必将导致全策略的最优化,这可由下面的Bellman方程看出。
fk(Sk)=opt(rk(Sk,Xk)?茌fk+1(Sk+1))fn+1(Sn+1)=0或1
Bellman方程可作如下解释:第K步子策略的最优性是由第K步的决策(注意:不是第K步的最优决策)与第K+1步的最优子策略产生的,即K+1步子策略的最优性必将导致K步子策略的最优性,K步子策略的最优性必将导致K-1步子策略的最优性,依此类推,直至1步子策略即全过程策略的最优性。
现在,再结合最短路问题来分析最优性原理。生活中的常识告诉我们,最短路有一个重要特性:如果由起点A经过H点和P点而到达终点T是一条最短路线,则由点H出发经过P点而到达终点T的这条子路线,对于从点H出发到达终点T的所有可能选择的不同路线来说,必定也是最短路线。此特性用反证法易证。因为如果不是这样,则从点H到T点有另一条距离更短的路线存在,把它和原来最短路线由A点到达H点的那部分连接起来,就会得到一条由A点到终点T的新路线,它比原来那条最短路线的距离还要短。这与假设矛盾,是不可能的。
因此,借助最短路径问题的相关常识,最优性原理可表述为:最短路径的子路径必然是最短的。
四、无记忆性与记忆性
在动态规划一章中,教师经常会提到“无记忆性”与“记忆性”两个看似完全矛盾的概念,不少学生也感到十分茫然。其实,这两个概念在动态规划中得到了完美的统一。
“无记忆性”指的是可用动态规划方法求解的多阶段决策问题,在划分阶段时,状态必须满足的一个特性,也称为无后效性或马尔科夫性。其实质是:某阶段的状态一旦确定,则此后过程的演变不再受此前各状态及决策的影响。即“未来与过去无关”,当前的状态是此前历史的一个完整总结,此前的历史只能通过当前的状态去影响过程未来的演变。[1]
“记性性”指的是用动态规划方法求解多阶段决策问题时(以逆序为例),为求得第K步最优子策略fk(Sk),必须先计算出从第K+1阶段的各状态出发所对应的最优子策略fk+1(Sk+1),并由第K+1步的最优子策略fk+1(Sk+1)去求取第K步最优子策略fk(Sk)。这些后续状态对应的最优子策略实际上构成了一张查找表(Lookup Table)。[3]为更好地理解无记忆性与记忆性,仍以最短路问题为例进行说明。
假设有一个可分为10个阶段的最短路问题,每阶段有10个状态可供选择。“无记忆性”指的是当游客在第k阶段处于状态Sk时,则该游客从Sk出发到终点的最短路径(K步最优子策略)只与Sk相关,而与Sk之前的状态、决策无任何关系。
“记忆性”指的是当用动态规划方法求解最短路问题时,第K步最优子策略是由第K步的决策和第K+1步的最优子策略共同决定的,而第K+1步的最优子策略已在之前求出并存放于内存之中,这就是记忆性。动态规划的记忆性可节省大量的计算时间,但会占用较多的计算机内存,即常用的“空间换时间”策略。
以上题为例,10个阶段每阶段10个状态的最短路问题,如果采用穷举法,则需要计算的路径条数(相当于动态规划中的全策略)为109条,每条路径需要进行10次加法运算;在109条路径中找出最短路径需要进行109-1次比较运算,则总的基本运算是11*109-1次。
而采用动态规划方法时,每阶段的每个状态需要进行10次加法运算和9次比较运算,则总的基本运算次数为1539次(其中加法运算810次,比较运算729次),和穷举法比较可节省大量的计算时间。
从该例题的分析可知,一个多阶段决策问题之所以可采用有“记忆性”的动态规划方法求解,恰恰是因为该问题在划分阶段时,各阶段的自然特征(即状态)满足“无记忆性”。因此,我们说,“记忆性”与“无记忆性”在动态规划中得到了完美的统一。
五、结束语
经教学实践证明,在动态规划教学中以最短路为引例,有利于学生对动态规划相关概念的理解,尤其有利于学生掌握最优性原理和无记忆性、记忆性这些晦涩难懂的原理与性质,为学生学好、用好动态规划打下了良好基础。
[ 参 考 文 献 ]
[1] 胡运权.运筹学教程(第四版)[M].北京:清华大学出版社,2012:191-232.
[2] Bellman R. E.Dynamical Programming[M].普林斯顿大学出版社,1957:58-92.
[3] Hamdy A. Taha. Operations Research:An introduction(第8版)[M].北京:人民邮电出版社,2008:744-754.
[4] 《运筹学》教材编写组.运筹学(第三版)[M].北京:清华大学出版社,2005:194-215.
[5] 韩伯棠.管理运筹学(第二版)[M].北京:高等教育出版社,2005:256-262.
[责任编辑:王 品]



[摘 要]在运筹学的分支体系中,动态规划因其应用的广泛性而占有十分重要的地位。针对动态规划教学中的难点,可以以最短路问题为引例,以大家耳熟能详的名称对动态规划中的基本概念进行阐释,并对最优性原理、无记忆性与记忆性进行比较系统的阐述,指出最优性原理表现在最短路问题中即是“最短路径的子路径必然是最短的”。最后,还可以以最短路分析动态规划求解时常用的“空间换时间”策略。
[关键词]动态规划;最优性原理;无记忆性;记忆性
[中图分类号] TP399 [文献标识码] A [文章编号] 2095-3437(2016)01-0108-02
在运筹学的分支体系中,动态规划因其应用的广泛性而占有十分重要的地位。但动态规划仅仅是解决某类特殊的多阶段决策问题的一种方法,不具有统一的数学模型和算法步骤[1],而且概念多,因此学生普遍反应“动态规划真的有用但确实难学”。本文以最短路问题为案例,对动态规划相关概念、最优性原理、无记忆性等进行了阐释。
一、案例的选择
可用动态规划求解的问题很多,如最短路、资源分配、生产与存储等,而最短路问题因其空间特征明显,易于划分阶段、易于描述每阶段开始和结束时的状态,以及在每个状态之下做出的决策、每次决策产生的决策指标值等,因此,对初学者而言,最易接受和理解的例子还是最短路问题。本文以最短路问题作为引例,帮助学生们理解和掌握动态规划的相关概念及基本方程、最优性原理等。
二、相关概念的解释
动态规划相关概念繁多,从阶段、状态开始,到过程指标函数,刚接触时,不少学生感到一头雾水,十分茫然。而借助于最短路问题,将动态规划的相关概念与最短路问题中大家耳熟能详的名称相对应,则十分有助于学生对动态规划基本概念的把握。相关概念具体对应关系如表1所示。
从上表可知,动态规划的基本概念在最短路问题中都可找到与之对应的解释,非常有助于学生掌握动态规划问题的实质。
三、最优性原理的解释
教材[1]对最优性原理作了如下表述:无论过去的决策和状态如何,对前面的决策所形成的当前状态而言,余下的决策序列必须构成最优策略,即最优策略的子策略总是最优的。
对最优性原理,部分学生将其理解为:组成最优策略的决策必须是最优的。产生这种误解的原因是将决策与策略相混淆。在动态规划中,决策指的是在某种状态下作出的一种选择,是一种瞬时行为。决策无优劣之分,每一步决策会产生一个决策指标值rk(Sk,Xk),它只是说明本次决策产生的益损值;而策略是由一系列决策所组成,策略是决策的集合,策略有优劣之分,度量策略优劣的数量指标值就是指标函数值fk(Sk)。一般而言,指标函数值是决策指标值的和或积的形式,即
fk(Sk)=opt(rj(Sj,Xj))或fk(Sk)=opt(rj(Sj,Xj))。
因此,单步决策的最优化一般不可能产生全策略的最优化,而子策略的最优化必将导致全策略的最优化,这可由下面的Bellman方程看出。
fk(Sk)=opt(rk(Sk,Xk)?茌fk+1(Sk+1))fn+1(Sn+1)=0或1
Bellman方程可作如下解释:第K步子策略的最优性是由第K步的决策(注意:不是第K步的最优决策)与第K+1步的最优子策略产生的,即K+1步子策略的最优性必将导致K步子策略的最优性,K步子策略的最优性必将导致K-1步子策略的最优性,依此类推,直至1步子策略即全过程策略的最优性。
现在,再结合最短路问题来分析最优性原理。生活中的常识告诉我们,最短路有一个重要特性:如果由起点A经过H点和P点而到达终点T是一条最短路线,则由点H出发经过P点而到达终点T的这条子路线,对于从点H出发到达终点T的所有可能选择的不同路线来说,必定也是最短路线。此特性用反证法易证。因为如果不是这样,则从点H到T点有另一条距离更短的路线存在,把它和原来最短路线由A点到达H点的那部分连接起来,就会得到一条由A点到终点T的新路线,它比原来那条最短路线的距离还要短。这与假设矛盾,是不可能的。
因此,借助最短路径问题的相关常识,最优性原理可表述为:最短路径的子路径必然是最短的。
四、无记忆性与记忆性
在动态规划一章中,教师经常会提到“无记忆性”与“记忆性”两个看似完全矛盾的概念,不少学生也感到十分茫然。其实,这两个概念在动态规划中得到了完美的统一。
“无记忆性”指的是可用动态规划方法求解的多阶段决策问题,在划分阶段时,状态必须满足的一个特性,也称为无后效性或马尔科夫性。其实质是:某阶段的状态一旦确定,则此后过程的演变不再受此前各状态及决策的影响。即“未来与过去无关”,当前的状态是此前历史的一个完整总结,此前的历史只能通过当前的状态去影响过程未来的演变。[1]
“记性性”指的是用动态规划方法求解多阶段决策问题时(以逆序为例),为求得第K步最优子策略fk(Sk),必须先计算出从第K+1阶段的各状态出发所对应的最优子策略fk+1(Sk+1),并由第K+1步的最优子策略fk+1(Sk+1)去求取第K步最优子策略fk(Sk)。这些后续状态对应的最优子策略实际上构成了一张查找表(Lookup Table)。[3]为更好地理解无记忆性与记忆性,仍以最短路问题为例进行说明。
假设有一个可分为10个阶段的最短路问题,每阶段有10个状态可供选择。“无记忆性”指的是当游客在第k阶段处于状态Sk时,则该游客从Sk出发到终点的最短路径(K步最优子策略)只与Sk相关,而与Sk之前的状态、决策无任何关系。
“记忆性”指的是当用动态规划方法求解最短路问题时,第K步最优子策略是由第K步的决策和第K+1步的最优子策略共同决定的,而第K+1步的最优子策略已在之前求出并存放于内存之中,这就是记忆性。动态规划的记忆性可节省大量的计算时间,但会占用较多的计算机内存,即常用的“空间换时间”策略。
以上题为例,10个阶段每阶段10个状态的最短路问题,如果采用穷举法,则需要计算的路径条数(相当于动态规划中的全策略)为109条,每条路径需要进行10次加法运算;在109条路径中找出最短路径需要进行109-1次比较运算,则总的基本运算是11*109-1次。
而采用动态规划方法时,每阶段的每个状态需要进行10次加法运算和9次比较运算,则总的基本运算次数为1539次(其中加法运算810次,比较运算729次),和穷举法比较可节省大量的计算时间。
从该例题的分析可知,一个多阶段决策问题之所以可采用有“记忆性”的动态规划方法求解,恰恰是因为该问题在划分阶段时,各阶段的自然特征(即状态)满足“无记忆性”。因此,我们说,“记忆性”与“无记忆性”在动态规划中得到了完美的统一。
五、结束语
经教学实践证明,在动态规划教学中以最短路为引例,有利于学生对动态规划相关概念的理解,尤其有利于学生掌握最优性原理和无记忆性、记忆性这些晦涩难懂的原理与性质,为学生学好、用好动态规划打下了良好基础。
[ 参 考 文 献 ]
[1] 胡运权.运筹学教程(第四版)[M].北京:清华大学出版社,2012:191-232.
[2] Bellman R. E.Dynamical Programming[M].普林斯顿大学出版社,1957:58-92.
[3] Hamdy A. Taha. Operations Research:An introduction(第8版)[M].北京:人民邮电出版社,2008:744-754.
[4] 《运筹学》教材编写组.运筹学(第三版)[M].北京:清华大学出版社,2005:194-215.
[5] 韩伯棠.管理运筹学(第二版)[M].北京:高等教育出版社,2005:256-262.
[责任编辑:王 品]

