面向缓冲区容量有限的AGV系统调度研究
熊晔+毛剑琳+郭宁+付丽霞

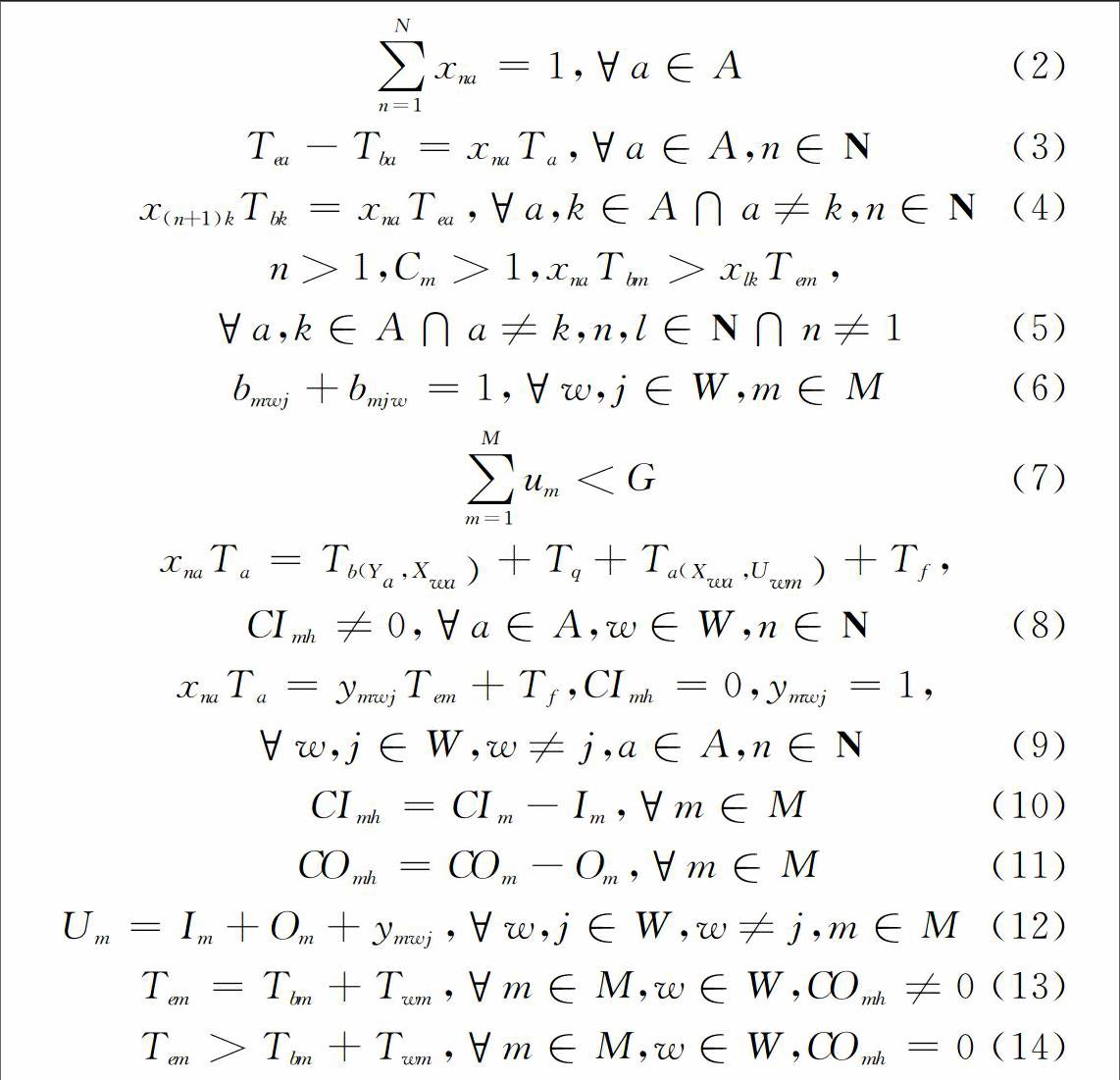
摘要:实际柔性制造系统中,由于加工区缓冲区容量有限,导致AGV配送任务时间延长,降低了系统工作效率。为解决此问题,建立缓冲区容量有限的AGV系统调度数学优化模型,提出混合灰狼遗传算法对AGV系统进行优化。新算法在传统遗传算法选择操作上,结合灰狼优化算法中的种群等级制度和灰狼狩猎机制,避免了传统精英策略中种群多样性变差的特点,增强了全局搜索能力。仿真结果表明:混合灰狼遗传算法较传统遗传算法具有更快的收敛速度,能得到更优解,提高AGV调度的效率,验证了相关改进机制的有效性。
关键词:柔性制造系统;AGV配送;缓冲区容量有限;AGV系统调度;混合灰狼遗传算法
DOIDOI:10.11907/rjdk.172156
中图分类号:TP319
文献标识码:A文章编号文章编号:1672-7800(2018)001-0152-05
Abstract:In the actual flexible manufacturing system, due to the limited capacity of the processing zone buffer, AGV delivery task time is prolonged, the processing cost is increased, and the working efficiency of the system is reduced. In order to solve this problem, a mathematical model of AGV system scheduling optimization with limited buffer capacity is established. A hybrid grey wolf optimization and genetic algorithm (HGWOGA) is proposed to optimize the AGV system. The new algorithm in the selection operation, combined with the gray wolf optimization algorithm in the population hierarchy and gray wolf hunting mechanism, to avoid the traditional elite strategies in the diversity of the characteristics of population diversity, and enhance the global search capabilities The simulation results show that the hybrid wolf genetic algorithm has faster convergence rate than traditional genetic algorithm, can get better solution, improve the efficiency of AGV scheduling, and verify the effectiveness of the relevant improvement mechanism.
Key Words:Flexible Manufacturing System (FMS); AGV distribution; limited buffer capacity; AGV system scheduling; HGWOGA
0引言
在柔性制造系統(Flexible Manufacturing System,FMS)中,自动化搬运系统有显著地位。常见的自动化搬运设备有堆垛机、传送带和自动导引小车(Automatic Guided Vehicle,AGV)等[1],而AGV有代替人工、节省成本;充电、驱动系统耗能少;能源利用率高、噪音低等优点[2]。在集成化生产环境中,AGV是连接仓库和生产车间的重要环节,成为FMS中不可或缺的重要组成部分。
传统AGV的研究大致分为两个方向:AGV系统的路径规划和AGV在车间的调度研究,但主要研究集中在AGV系统路径和生产效率优化方面[3],AGV在车间调度中的影响研究较少。乔岩[4]等研究了基于改进时间窗的AGVs的避障路径规划。谷宝慧[5]针对AGV载重和运送货箱体积限定问题建立AGV路径优化模型,利用改进的量子微粒群算法实现。刘旭[6]等针对多AGV在混流作业车间配送物料问题,运用一种改进的遗传算法来进行求解。Nishi[7]等针对柔性制造系统中多AGV路径规划问题,建立多AGV调度模型,提出了一种分解算法进行求解。杜亚江[8]等建立了复杂约束的AGV多参数问题数学模型,采用混合遗传算法优化了调度时间。
上述研究中有多数未考虑加工区缓冲区容量有限的情况,针对AGV在物料配送、AGV路径最优的方面进行研究,而在实际生产应用中,很多情况下加工区的缓冲区是有限的,并且存在大量的单AGV的生产系统,因此对FMS中的加工区缓冲区容量的单AGV调度进行研究具有十分重要的理论和应用价值[9]。
本文对缓冲区容量有限的单AGV系统调度问题进行了分析,建立了问题优化模型,分析了模型的特点。针对优化模型提出了混合灰狼遗传算法,在传统遗传算法的选择算子中引入了灰狼优化算法中灰狼社会等级、狩猎机制理念进行求解。模拟实验结果显示:本文提出的混合灰狼遗传算法具有有效性。
1AGV调度问题
1.1问题描述
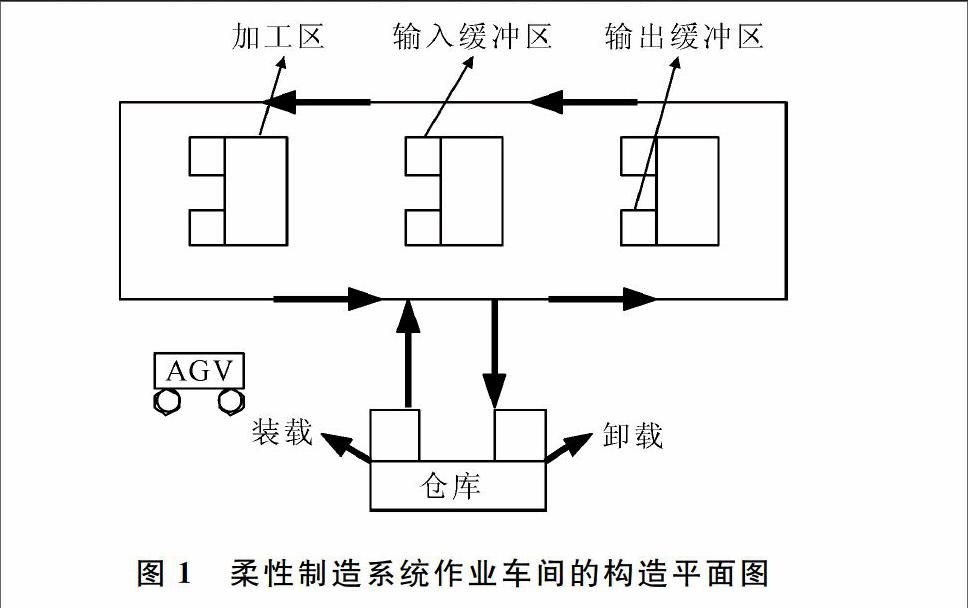
一个典型的柔性制造系统作业车间包括AGV小车、缓冲区有限的加工区、导向网络和仓库,其平面构造图如图1所示。AGV进入FMS的先后顺序是确定的,并视作AGV在系统中的流动路线为一个循环,制件从仓库出发,按加工次序依次流经各个加工机器进行加工最终回到仓库。AGV小车将制件w从当前加工区移动到目标加工区m上的一个过程定义为一次搬运任务。
在一个给定的柔性制造系统中,有一台自动导引车和一个制件集,目标是使得完成整个过程的时间最短,计算每个制件在每台机器的加工时间和每个输入/输出缓冲区的时间,确定每个机器与机器之间所走路程的起始和完成时间。
為了便于研究,作如下假设:
(1)AGV一次仅执行一次任务。
(2)每个加工区每次只加工一个制件。
(3)输入缓冲区和输出缓冲区容量有限不为零且相等。
(4)制件在整个加工过程中不中止。
(5)自动导引车的起始位置处于仓库缓冲区内,等待自动导引车执行完当前任务后,驶入并停在刚执行完的任务的缓冲区内,等待指令,准备执行另一个任务。
1.2调度模型
M:加工区集:
W:制件集;
A:搬运任务集;
N:任务次序集;
G:系统允许的最大制件量;
m:加工区编号,m∈M,Mo表示仓库;
w:制件编号,w∈W;
A:任务编号,a∈A;
n:任务执行的次序编号,n∈N;
CIm:加工区m的输入缓冲区容量,CIm>0;
COm:加工区m的输出缓冲区容量,COm=CIm;
CImh:加工区m的输入缓冲区的剩余可容纳制件的量;
Im:加工区m的输入缓冲区上的制件个数;
COmh:加工区m的输出缓冲区的剩余可容纳制件的量;
Cm:加工区m的输出缓冲区上的制件数;
Um:表示在加工区m上现有的制件数;
Twm:制件w在加工区m上的加工时间;
Uwm:表示制件w在加工区m上加工;
Tbm:为制件w在加工区m上的开始加工时间;
Tem:为制件w在加工区m上的结束加工时间;
Tq:AGV装载制件的固定时间;
Tf:AGV卸载制件的固定时间;
Tba:AGV的搬运任务a的开始时间;
Tea:AGV的搬运任务a的结束时间;
Xwa:搬运任务a开始时制件w所在的加工区;
Ya:AGV的搬运任务a开始时AGV所在的加工区;
Tb(m1,m2):AGV从加工区m1移动到m2的所用时间;
Ta:AGV执行任务a所用的时间。
式(1)表示AGV完成调度集内全部任务所用时间最短;式(2)是AGV每次完成且只完成一个任务。式(3)是搬运任务a的结束时间减去搬运任务a的开始时间即为AGV完成一次搬运任务所耗费的时间;式(4)是后一个任务开始时间等于前一个任务的结束时间;式(5)表示加工区的输出缓冲区上有多个制件,则存在一个加工区分配多个搬运任务时,在调度时段,相同加工区的任务只能按分配时间的先后执行。式(6)是一个加工区一次只能加工一个制件;式(7)表示系统的现有制件数不可超过系统承受的最大制件数;式(8)表示输入缓冲区的容量不满时,完成一次搬运任务所耗时等价于小车从当前位置空载移动到目标制件所在的加工区加上目标制件装载的时间再加上AGV移动到目标加工区的输入缓冲区的时间和目标制件卸载的时间;式(9)表示输入缓冲区的剩余容量为零时,AGV完成一次搬运任务所耗时等价于在目标加工区上的制件的结束加工时间加上目标制件卸载的时耗;式(10)和(11)表示输入/输出缓冲区容量减去输入/输出缓冲区上的制件数即是输入/输出缓冲区的剩余容量;式(12)输入缓冲区的制件数加上输出缓存区上的制件再加上加工区上正在加工的制件数即加工区现有的制件数;式(13)表示加工区的输出缓存器剩余容量不为零时,制件的加工结束时间等于制件的加工开始时间加上制件在加工区上的加工时间;式(14)表示加工区的输出缓存器为满时,制件加工完毕之后需等候进入输出缓存区。
2混合灰狼遗传算法
灰狼优化算法(Gery Wolf Optimization,GWO)是由Mirjalili S等[10]在2014年提出的新算法,原理为模仿自然界灰狼种群领导层级和以及狼群跟踪、包围猎物的狩猎过程来实现优化。GWO算法能在解空间中快速找出最优解,避免出现局部最优[11]。
本文将GWO算法中灰狼社会等级、狩猎机制引入至标准遗传算法的选择算子中,来克服了传统的遗传算法易早熟的缺点,从而提高了算法全局搜索的效率。新算法流程如图2所示。
2.1编码与解码
本文研究的是AGV任务排序问题,则选择加工区的序数方式进行编码,将搬运任务集内的任务数中加工区进行排序,AGV小车任务的先后顺序按照加工区序号执行,同一个加工区使用相同的编号。例如:某染色体的编码为“3 5 1 4 3 6 2 3”(如图3所示)。
2.2适应度函数
缓冲区容量有限的AGV 调度模型适应度函数设计为:
2.3选择算子设计
本文是采用轮盘赌和精英选择策略结合的方式。如果不采用精英保留策略,仅是采用轮盘赌选择算子,这样就会导致优良的个体丢失,为了解决这个矛盾引入灰狼优化算法的理念。
在每一次选择操作的时候保留α,β,δ 3种个体,形成如图4所示的灰狼内部社会层级地位,三者适应度关系满足式(16)。剩余的个体即是ω,整个种群在α,β,δ的领导下向全局最优解进化。
Xα表示α当前位置,Xβ表示β当前位置,Xδ表示δ当前位置,X(t) 表示第t代灰狼的位置向量。由式(22)-式(27) 计算出个体与α,β,δ的距离,然后由式(28)即可定义出猎物的最终方位。
改进后的选择步骤如下:
step1:初始化随机狼群。
step2:计算出每头狼对应的适应度值。
step3:将适应度排列前三的灰狼个体位置分别记为α,β,δ。
step4:按照式(22)-(24)计算其它个体与α,β,δ的距离,并根据式(25)-(28)计算每个灰狼个体的位置。
step5:更新参数a,A,C等参数的值。
step6:如不满足结束条件,转到第二步。
step7:导出α狼的位置。
step8:按轮盘赌规则选择个体复制到下一代
2.4交叉算子设计
本文采用了部分映射交叉方式,随机产生两个随机数p,q∈[2,n-1],交换两个染色体i和j位于p和q之间的基因片段,映射交叉操作如图6所示[12]。为了分散开染色体上的基因,不让其聚集在一个小的范围,交叉操作之后要检验子代的染色体上相邻基因的距离,两个基因距离小于一定值时便认为两个基因重复,在原基因的邻域产生一个新的基因替换原来的基因。
2.5变异算子设计
本文中的变异方法采用倒置变异[13],也就是在染色体上随机选择两个位置,然后颠倒两个基因序列。如图7所示。
3仿真实验与分析
为验证混合灰狼遺传算法的有效性,本文以某柔性制造车间为例,设计一组仿真实验。该FMS中存在五个加工区,加上一个仓库,每个加工区均配有容量为3的输入缓冲区F1和容量为3的输出缓冲区F2。制件从仓库出发,经过加工区后运回,仓库加工区分别用a、b、c、d、e表示,仓库用0来表示。
AGV的移动路径时间如表1所示。
通过Matlab进行实验仿真,使用传统的遗传算法和本文设计的混合灰狼遗传算法对缓冲区容量有限的AGV调度模型求解,得出AGV配送及加工完成所有制件的总时间。参数设置如下:初始种群规模为50;交叉概率Pc为0.6;变异概率Pm为0.01;在制件数不同的情况下,仿真结果如表2所示。标记为HGWOGA最优解、GA最优
解的列表示为分别采用HGWOGA和GA算法进行调度后AGV配送及加工完成所有制件的总时间(s),H/G列表示HGWOGA相对于GA算法提高AGV调度系统的比率。
由表2可看出,当制件数小于15时,两种算法都能得到相同的最优解,但是随着制件数的增加,当制件数大于15时,HGWOGA算法的调度时间要远小于GA算法的调度时间,且平均能提高5%左右的调度效率,这能够说明本文所提出的混合灰狼遗传算法对缓冲区容量有限的AGV调度模型的改进策略是有效的。
由图8,图9可以看出,当制件数为15时,GA算法在20代左右收敛,HGWOGA算法在10代左右就已经达到收敛;当制件数为20时,GA算法在60代左右收敛,HGWOGA算法在20代左右就已经达到收敛,HGWOGA算法的收敛速度要远远快于GA算法的收敛速度,且能得到更好的最优解。这也能说明HGWOGA算法的有效性。
4结语
本文针对FMS中缓冲区容量有限的单AGV调度模型,通过将灰狼优化算法中的社会等级、狩猎制度引入传统的遗传算法中,提出了一种全新的混合灰狼遗传算法,极大的提升了算法的搜索能力。仿真实验结果表明:HGWOGA算法相对于传统的遗传算法能有效求解缓冲区容量有限的单AGV调度的问题,具有收敛速度快、得到调度更优解及提升AGV调度效率的优点。但在实际生产中,存在大量的有限缓冲区的多AGV的情况,在进一步的科研中,这些情况亟待深入研究。
参考文献:
[1]杨锋英,刘会超.AGV作业调度模型及改进的DE算法研究[J].计算机工程与应用,2014,50(9):225-230.
[2]王皖君,张为公.自动导引车导引技术研究现状与发展趋势[J].传感器与微系统,2009,28(12):5-7.
[3]任乃飞,于璐.基于混合遗传算法的协同制造系统调度研究[J].电子科技,2016,29(6):29-33.
[4]乔岩,钱晓明,楼佩煌.基于改进时间窗的AGVs避碰路径规划[J].计算机集成制造系统,2012,18(12):2683-2688.
[5]汤旻安,谷宝慧.改进PSO在AGV系统路径优化调度中的应用研究[J].计算机工程与应用,2016,52(3):261-265.
[6]刘旭,楼佩煌,钱晓明,等.基于改进遗传算法的物料配送多AGV调度优化[J].机械设计与制造工程,2015(3):16-21.
[7]NISHI T, HIRANAKA Y, GROSSMANN I E. A bilevel decomposition algorithm for simultaneous production scheduling and conflict-free routing for automated guided vehicles[J]. Computers & Operations Research,2011,38(5):876-888.
[8]杜亚江,郑向东,亢丽君.基于遗传禁忌搜索算法的AGV物料输送调度问题研究[J].物流科技,2013,36(7):1-4.
[9]周巧.面向缓存有限的柔性制造系统单AGV调度研究[D].广东工业大学,2014.
[10]MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software,2014,69(3):46-61.
[11]龙文,赵东泉,徐松金.求解约束优化问题的改进灰狼优化算法[J].计算机应用,2015,35(9):2590-2595.
[12]黄英杰.基于目标级联法和智能优化算法的车间调度问题研究[D].华南理工大学,2012.
[13]霍凯歌,张亚琦,胡志华.自动化集装箱码头多载AGV调度问题研究[J].大连理工大学学报,2016,56(3):244-251.
(责任编辑:刘亭亭)


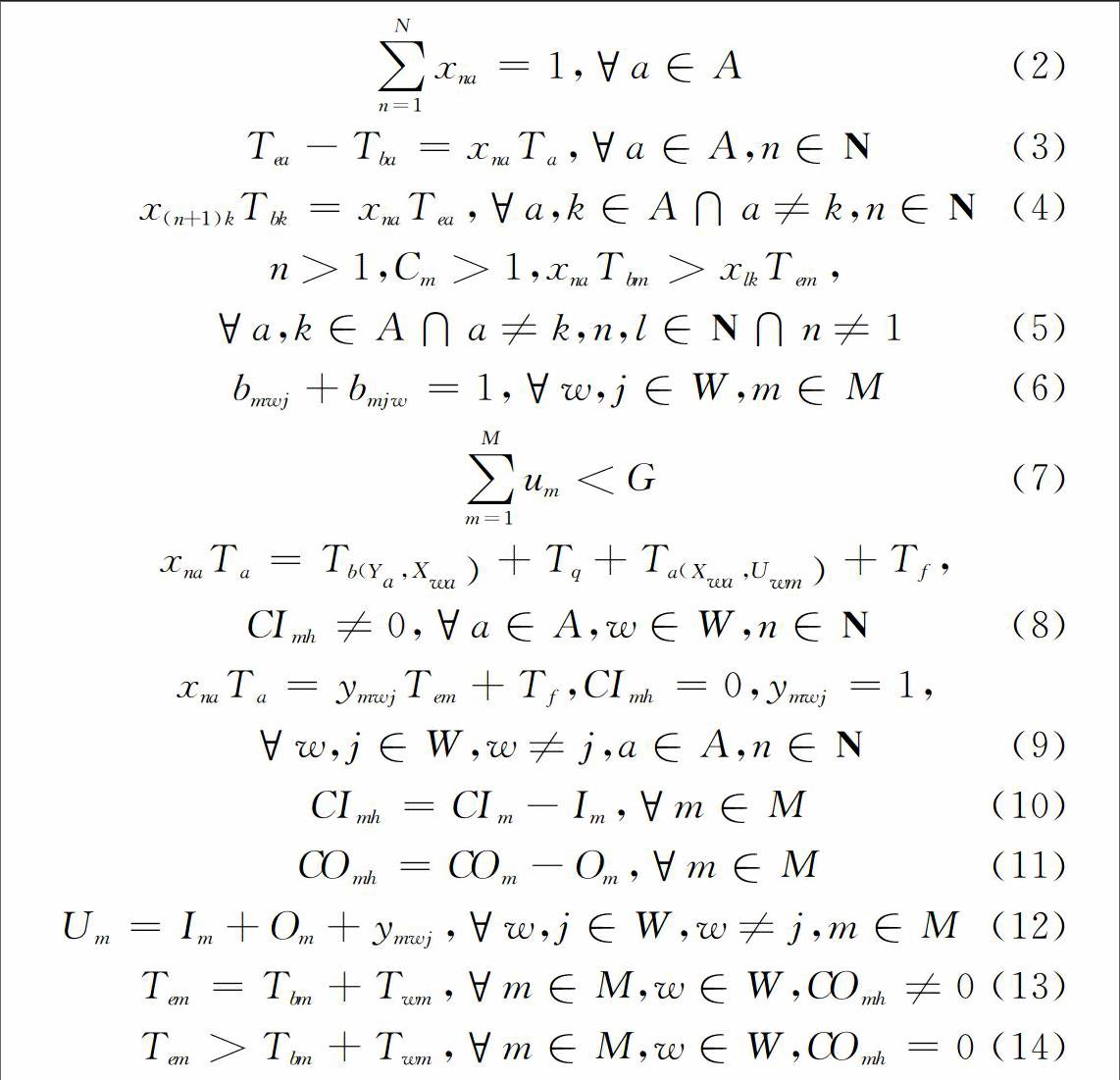
摘要:实际柔性制造系统中,由于加工区缓冲区容量有限,导致AGV配送任务时间延长,降低了系统工作效率。为解决此问题,建立缓冲区容量有限的AGV系统调度数学优化模型,提出混合灰狼遗传算法对AGV系统进行优化。新算法在传统遗传算法选择操作上,结合灰狼优化算法中的种群等级制度和灰狼狩猎机制,避免了传统精英策略中种群多样性变差的特点,增强了全局搜索能力。仿真结果表明:混合灰狼遗传算法较传统遗传算法具有更快的收敛速度,能得到更优解,提高AGV调度的效率,验证了相关改进机制的有效性。
关键词:柔性制造系统;AGV配送;缓冲区容量有限;AGV系统调度;混合灰狼遗传算法
DOIDOI:10.11907/rjdk.172156
中图分类号:TP319
文献标识码:A文章编号文章编号:1672-7800(2018)001-0152-05
Abstract:In the actual flexible manufacturing system, due to the limited capacity of the processing zone buffer, AGV delivery task time is prolonged, the processing cost is increased, and the working efficiency of the system is reduced. In order to solve this problem, a mathematical model of AGV system scheduling optimization with limited buffer capacity is established. A hybrid grey wolf optimization and genetic algorithm (HGWOGA) is proposed to optimize the AGV system. The new algorithm in the selection operation, combined with the gray wolf optimization algorithm in the population hierarchy and gray wolf hunting mechanism, to avoid the traditional elite strategies in the diversity of the characteristics of population diversity, and enhance the global search capabilities The simulation results show that the hybrid wolf genetic algorithm has faster convergence rate than traditional genetic algorithm, can get better solution, improve the efficiency of AGV scheduling, and verify the effectiveness of the relevant improvement mechanism.
Key Words:Flexible Manufacturing System (FMS); AGV distribution; limited buffer capacity; AGV system scheduling; HGWOGA
0引言
在柔性制造系統(Flexible Manufacturing System,FMS)中,自动化搬运系统有显著地位。常见的自动化搬运设备有堆垛机、传送带和自动导引小车(Automatic Guided Vehicle,AGV)等[1],而AGV有代替人工、节省成本;充电、驱动系统耗能少;能源利用率高、噪音低等优点[2]。在集成化生产环境中,AGV是连接仓库和生产车间的重要环节,成为FMS中不可或缺的重要组成部分。
传统AGV的研究大致分为两个方向:AGV系统的路径规划和AGV在车间的调度研究,但主要研究集中在AGV系统路径和生产效率优化方面[3],AGV在车间调度中的影响研究较少。乔岩[4]等研究了基于改进时间窗的AGVs的避障路径规划。谷宝慧[5]针对AGV载重和运送货箱体积限定问题建立AGV路径优化模型,利用改进的量子微粒群算法实现。刘旭[6]等针对多AGV在混流作业车间配送物料问题,运用一种改进的遗传算法来进行求解。Nishi[7]等针对柔性制造系统中多AGV路径规划问题,建立多AGV调度模型,提出了一种分解算法进行求解。杜亚江[8]等建立了复杂约束的AGV多参数问题数学模型,采用混合遗传算法优化了调度时间。
上述研究中有多数未考虑加工区缓冲区容量有限的情况,针对AGV在物料配送、AGV路径最优的方面进行研究,而在实际生产应用中,很多情况下加工区的缓冲区是有限的,并且存在大量的单AGV的生产系统,因此对FMS中的加工区缓冲区容量的单AGV调度进行研究具有十分重要的理论和应用价值[9]。
本文对缓冲区容量有限的单AGV系统调度问题进行了分析,建立了问题优化模型,分析了模型的特点。针对优化模型提出了混合灰狼遗传算法,在传统遗传算法的选择算子中引入了灰狼优化算法中灰狼社会等级、狩猎机制理念进行求解。模拟实验结果显示:本文提出的混合灰狼遗传算法具有有效性。
1AGV调度问题
1.1问题描述
一个典型的柔性制造系统作业车间包括AGV小车、缓冲区有限的加工区、导向网络和仓库,其平面构造图如图1所示。AGV进入FMS的先后顺序是确定的,并视作AGV在系统中的流动路线为一个循环,制件从仓库出发,按加工次序依次流经各个加工机器进行加工最终回到仓库。AGV小车将制件w从当前加工区移动到目标加工区m上的一个过程定义为一次搬运任务。
在一个给定的柔性制造系统中,有一台自动导引车和一个制件集,目标是使得完成整个过程的时间最短,计算每个制件在每台机器的加工时间和每个输入/输出缓冲区的时间,确定每个机器与机器之间所走路程的起始和完成时间。
為了便于研究,作如下假设:
(1)AGV一次仅执行一次任务。
(2)每个加工区每次只加工一个制件。
(3)输入缓冲区和输出缓冲区容量有限不为零且相等。
(4)制件在整个加工过程中不中止。
(5)自动导引车的起始位置处于仓库缓冲区内,等待自动导引车执行完当前任务后,驶入并停在刚执行完的任务的缓冲区内,等待指令,准备执行另一个任务。
1.2调度模型
M:加工区集:
W:制件集;
A:搬运任务集;
N:任务次序集;
G:系统允许的最大制件量;
m:加工区编号,m∈M,Mo表示仓库;
w:制件编号,w∈W;
A:任务编号,a∈A;
n:任务执行的次序编号,n∈N;
CIm:加工区m的输入缓冲区容量,CIm>0;
COm:加工区m的输出缓冲区容量,COm=CIm;
CImh:加工区m的输入缓冲区的剩余可容纳制件的量;
Im:加工区m的输入缓冲区上的制件个数;
COmh:加工区m的输出缓冲区的剩余可容纳制件的量;
Cm:加工区m的输出缓冲区上的制件数;
Um:表示在加工区m上现有的制件数;
Twm:制件w在加工区m上的加工时间;
Uwm:表示制件w在加工区m上加工;
Tbm:为制件w在加工区m上的开始加工时间;
Tem:为制件w在加工区m上的结束加工时间;
Tq:AGV装载制件的固定时间;
Tf:AGV卸载制件的固定时间;
Tba:AGV的搬运任务a的开始时间;
Tea:AGV的搬运任务a的结束时间;
Xwa:搬运任务a开始时制件w所在的加工区;
Ya:AGV的搬运任务a开始时AGV所在的加工区;
Tb(m1,m2):AGV从加工区m1移动到m2的所用时间;
Ta:AGV执行任务a所用的时间。
式(1)表示AGV完成调度集内全部任务所用时间最短;式(2)是AGV每次完成且只完成一个任务。式(3)是搬运任务a的结束时间减去搬运任务a的开始时间即为AGV完成一次搬运任务所耗费的时间;式(4)是后一个任务开始时间等于前一个任务的结束时间;式(5)表示加工区的输出缓冲区上有多个制件,则存在一个加工区分配多个搬运任务时,在调度时段,相同加工区的任务只能按分配时间的先后执行。式(6)是一个加工区一次只能加工一个制件;式(7)表示系统的现有制件数不可超过系统承受的最大制件数;式(8)表示输入缓冲区的容量不满时,完成一次搬运任务所耗时等价于小车从当前位置空载移动到目标制件所在的加工区加上目标制件装载的时间再加上AGV移动到目标加工区的输入缓冲区的时间和目标制件卸载的时间;式(9)表示输入缓冲区的剩余容量为零时,AGV完成一次搬运任务所耗时等价于在目标加工区上的制件的结束加工时间加上目标制件卸载的时耗;式(10)和(11)表示输入/输出缓冲区容量减去输入/输出缓冲区上的制件数即是输入/输出缓冲区的剩余容量;式(12)输入缓冲区的制件数加上输出缓存区上的制件再加上加工区上正在加工的制件数即加工区现有的制件数;式(13)表示加工区的输出缓存器剩余容量不为零时,制件的加工结束时间等于制件的加工开始时间加上制件在加工区上的加工时间;式(14)表示加工区的输出缓存器为满时,制件加工完毕之后需等候进入输出缓存区。
2混合灰狼遗传算法
灰狼优化算法(Gery Wolf Optimization,GWO)是由Mirjalili S等[10]在2014年提出的新算法,原理为模仿自然界灰狼种群领导层级和以及狼群跟踪、包围猎物的狩猎过程来实现优化。GWO算法能在解空间中快速找出最优解,避免出现局部最优[11]。
本文将GWO算法中灰狼社会等级、狩猎机制引入至标准遗传算法的选择算子中,来克服了传统的遗传算法易早熟的缺点,从而提高了算法全局搜索的效率。新算法流程如图2所示。
2.1编码与解码
本文研究的是AGV任务排序问题,则选择加工区的序数方式进行编码,将搬运任务集内的任务数中加工区进行排序,AGV小车任务的先后顺序按照加工区序号执行,同一个加工区使用相同的编号。例如:某染色体的编码为“3 5 1 4 3 6 2 3”(如图3所示)。
2.2适应度函数
缓冲区容量有限的AGV 调度模型适应度函数设计为:
2.3选择算子设计
本文是采用轮盘赌和精英选择策略结合的方式。如果不采用精英保留策略,仅是采用轮盘赌选择算子,这样就会导致优良的个体丢失,为了解决这个矛盾引入灰狼优化算法的理念。
在每一次选择操作的时候保留α,β,δ 3种个体,形成如图4所示的灰狼内部社会层级地位,三者适应度关系满足式(16)。剩余的个体即是ω,整个种群在α,β,δ的领导下向全局最优解进化。
Xα表示α当前位置,Xβ表示β当前位置,Xδ表示δ当前位置,X(t) 表示第t代灰狼的位置向量。由式(22)-式(27) 计算出个体与α,β,δ的距离,然后由式(28)即可定义出猎物的最终方位。
改进后的选择步骤如下:
step1:初始化随机狼群。
step2:计算出每头狼对应的适应度值。
step3:将适应度排列前三的灰狼个体位置分别记为α,β,δ。
step4:按照式(22)-(24)计算其它个体与α,β,δ的距离,并根据式(25)-(28)计算每个灰狼个体的位置。
step5:更新参数a,A,C等参数的值。
step6:如不满足结束条件,转到第二步。
step7:导出α狼的位置。
step8:按轮盘赌规则选择个体复制到下一代
2.4交叉算子设计
本文采用了部分映射交叉方式,随机产生两个随机数p,q∈[2,n-1],交换两个染色体i和j位于p和q之间的基因片段,映射交叉操作如图6所示[12]。为了分散开染色体上的基因,不让其聚集在一个小的范围,交叉操作之后要检验子代的染色体上相邻基因的距离,两个基因距离小于一定值时便认为两个基因重复,在原基因的邻域产生一个新的基因替换原来的基因。
2.5变异算子设计
本文中的变异方法采用倒置变异[13],也就是在染色体上随机选择两个位置,然后颠倒两个基因序列。如图7所示。
3仿真实验与分析
为验证混合灰狼遺传算法的有效性,本文以某柔性制造车间为例,设计一组仿真实验。该FMS中存在五个加工区,加上一个仓库,每个加工区均配有容量为3的输入缓冲区F1和容量为3的输出缓冲区F2。制件从仓库出发,经过加工区后运回,仓库加工区分别用a、b、c、d、e表示,仓库用0来表示。
AGV的移动路径时间如表1所示。
通过Matlab进行实验仿真,使用传统的遗传算法和本文设计的混合灰狼遗传算法对缓冲区容量有限的AGV调度模型求解,得出AGV配送及加工完成所有制件的总时间。参数设置如下:初始种群规模为50;交叉概率Pc为0.6;变异概率Pm为0.01;在制件数不同的情况下,仿真结果如表2所示。标记为HGWOGA最优解、GA最优
解的列表示为分别采用HGWOGA和GA算法进行调度后AGV配送及加工完成所有制件的总时间(s),H/G列表示HGWOGA相对于GA算法提高AGV调度系统的比率。
由表2可看出,当制件数小于15时,两种算法都能得到相同的最优解,但是随着制件数的增加,当制件数大于15时,HGWOGA算法的调度时间要远小于GA算法的调度时间,且平均能提高5%左右的调度效率,这能够说明本文所提出的混合灰狼遗传算法对缓冲区容量有限的AGV调度模型的改进策略是有效的。
由图8,图9可以看出,当制件数为15时,GA算法在20代左右收敛,HGWOGA算法在10代左右就已经达到收敛;当制件数为20时,GA算法在60代左右收敛,HGWOGA算法在20代左右就已经达到收敛,HGWOGA算法的收敛速度要远远快于GA算法的收敛速度,且能得到更好的最优解。这也能说明HGWOGA算法的有效性。
4结语
本文针对FMS中缓冲区容量有限的单AGV调度模型,通过将灰狼优化算法中的社会等级、狩猎制度引入传统的遗传算法中,提出了一种全新的混合灰狼遗传算法,极大的提升了算法的搜索能力。仿真实验结果表明:HGWOGA算法相对于传统的遗传算法能有效求解缓冲区容量有限的单AGV调度的问题,具有收敛速度快、得到调度更优解及提升AGV调度效率的优点。但在实际生产中,存在大量的有限缓冲区的多AGV的情况,在进一步的科研中,这些情况亟待深入研究。
参考文献:
[1]杨锋英,刘会超.AGV作业调度模型及改进的DE算法研究[J].计算机工程与应用,2014,50(9):225-230.
[2]王皖君,张为公.自动导引车导引技术研究现状与发展趋势[J].传感器与微系统,2009,28(12):5-7.
[3]任乃飞,于璐.基于混合遗传算法的协同制造系统调度研究[J].电子科技,2016,29(6):29-33.
[4]乔岩,钱晓明,楼佩煌.基于改进时间窗的AGVs避碰路径规划[J].计算机集成制造系统,2012,18(12):2683-2688.
[5]汤旻安,谷宝慧.改进PSO在AGV系统路径优化调度中的应用研究[J].计算机工程与应用,2016,52(3):261-265.
[6]刘旭,楼佩煌,钱晓明,等.基于改进遗传算法的物料配送多AGV调度优化[J].机械设计与制造工程,2015(3):16-21.
[7]NISHI T, HIRANAKA Y, GROSSMANN I E. A bilevel decomposition algorithm for simultaneous production scheduling and conflict-free routing for automated guided vehicles[J]. Computers & Operations Research,2011,38(5):876-888.
[8]杜亚江,郑向东,亢丽君.基于遗传禁忌搜索算法的AGV物料输送调度问题研究[J].物流科技,2013,36(7):1-4.
[9]周巧.面向缓存有限的柔性制造系统单AGV调度研究[D].广东工业大学,2014.
[10]MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software,2014,69(3):46-61.
[11]龙文,赵东泉,徐松金.求解约束优化问题的改进灰狼优化算法[J].计算机应用,2015,35(9):2590-2595.
[12]黄英杰.基于目标级联法和智能优化算法的车间调度问题研究[D].华南理工大学,2012.
[13]霍凯歌,张亚琦,胡志华.自动化集装箱码头多载AGV调度问题研究[J].大连理工大学学报,2016,56(3):244-251.
(责任编辑:刘亭亭)

