基于KMeans聚类的微生物群落结构研究
王侠林+贺建峰


摘要:
随着宏基因组学的不断发展,揭示了微生物菌群在研究中的重要作用。采用K-Means聚类算法对来源于北平顶猴阴道微生物群落OTUs数据集的27个样本进行研究,并与PCA主成分分析法进行对比。K-Means聚类将OTUs数据集分成4个Cluster,而PCA将OTUs数据集划分成5个Cluster。此外,结合样本的元数据-pH,发现样本间的pH值相似性更能与K-Means聚类的分类保持一致。相较于PCA主成分析方法,K-Means聚类能更精确地对OTUs数据集进行分类。
关键词:
K-Means聚类;PCA主成分分析法;微生物群落结构;OTUs数据集
DOIDOI:10.11907/rjdk.172732
中图分类号:TP319
文献标识码:A文章编号文章编号:1672-7800(2018)001-0146-03
Abstract:The development of macrogeome has shown that microbial flora plays an important role in the research and development of many aspects. A total of 27 samples from the OTUs data collection of the microbiological community of the North Mongolian monkey were studied by K-Means clustering algorithm and compared with the PCA principal component analysis method. K-Means clustering divides the OTUs data set into four clusters. Interestingly, PCA divides the OTUs data set into five clusters. In addition, combining the sample metadata-pH, it is found that the pH similarity between the samples is more consistent with the classification of K-Means clustering.K-Means clustering classifies the OTUs data sets more accurately than the PCA principal analysis method.
Key Words:K-Means clustering; principal component analysis; microbial community structure; OTUs data set
0引言
微生物群落的种群多样性一直是微生物生态学和环境学科研究的重点。近年来,微生物群落结构成为了研究热点。群落结构决定了生态功能的特性和强弱,因此群落结构的高稳定性是实现生态功能的重要因素,群落结构变化也是标记环境变化的重要指标[1-4]。通过对目标微生物的群落结构和多样性进行解析并研究其动态变化,可为挖掘群落功能信息、优化群落结构与调节群落功能提供可靠依据。
自新一代高通量测序技术2005年问世以来,以其数字化信號、高数据通量、高准确率以及信息量丰富等优点,被广泛应用于微生物菌群研究中[3-6]。本次研究的菌群数据集具有OTUs(Operational Taxonomic Unit)数量多、数据量大、样本信息复杂以及具有一定稀疏性等特点,且微生物群落数据特性与文本分析的变化模式类似。因此,本文提出一种非监督学习算法K-Means聚类算法对微生物群落进行研究。
目前,在微生物群落研究中,PCA主成分分析法也是一种常用方法。PCA 主成分分析法是把多指标转化为少数几个综合指标,使其尽可能多地保留原始变量信息,且彼此不相关[7-8]。但处理结果具有一定模糊性,不能很好地抓住数据的真实子空间结构,当遮挡幅值较大时,效果较差。而K-Means聚类算法是一种非监督学习的硬聚类算法[9],是典型的基于原型的目标函数聚类方法的代表。它是以数据点到原型的某种距离作为优化的目标函数,利用函数求极值的方法得到迭代运算的调整规则,主要采用误差平方和准则函数作为聚类准则函数,以欧式距离作为相似度测度,具有计算速度快、操作简单、时间复杂度近似线性的特点,适合挖掘大规模数据集,且对大数据集分析有较高效率以及可伸缩性[10]。因此,本文采用K-Means聚类分析不同来源或不同时期的微生物群落,并与PCA方法进行对比,使该方法能够进一步运用于微生物研究。
1材料与方法
1.1数据来源
本次数据集来源于两个成年雌性北平顶猴个体PMA和PMB的阴道菌群数据,共27个样本。其中,PMA含有13个时间点数据,PMB含有14个时间点数据[11]。
1.2K-Means聚类原理
K-Means聚类[12-13]也称为K-平均或K-均值,是一种使用最广泛的聚类算法。它是将各个聚类子集内的所有数据样本均值作为该聚类的代表点,算法的主要思想是通过迭代过程把数据集划分为不同类别,使评价聚类性能的准则函数达到最优,从而使生成的每个聚类类内紧凑,类间独立。划分聚类方法对数据集进行聚类时包括如下3个要点:
(1)选定某种距离作为数据样本间的相似性度量。由于K-Means聚类算法不适合处理离散型属性,而对于连续型属性比较适合。因此,在计算数据样本之间的距离时,可以根据实际需要选择欧式距离、曼哈顿距离或者明考斯距离中的一种作为算法的相似性度量[14],其中最常用的是欧式距离。
(3)根據一个簇中对象的平均值进行相似度计算,步骤为:①将所有对象随机分配到k个非空的簇中;②然后计算每个簇的平均值,并用该平均值代表相应的簇;③根据每个对象与各个簇中心的距离,分配给最近的簇;④最后转到②,重新计算每个簇的平均值。该过程不断重复,直到满足某个准则函数才停止。
K-Means聚类的具体算法步骤[17]为:①为每个聚类确定一个初始聚类中心,共有k个初始聚类中心;②将样本集中的样本按照最小距离原则分配到最邻近聚类;③使用每个聚类中的样本均值作为新的聚类中心;④重复步骤②、③,直到聚类中心不再变化;⑤结束,得到k个聚类。
2分析结果
2.1K-Means聚类结果
利用K-Means聚类对北平顶猴OTUs数据集的27个样本进行分析,并通过MEV软件进行计算处理,最终将OTUs数据集分成了4类(见图1)。图1(a)、(b)、(c)、(d)分别表示K-Means聚类的4个Cluster。每行表示每个OTUs在不同样本中的相对丰度,每列表示每个样本中OTUs的相对丰度。
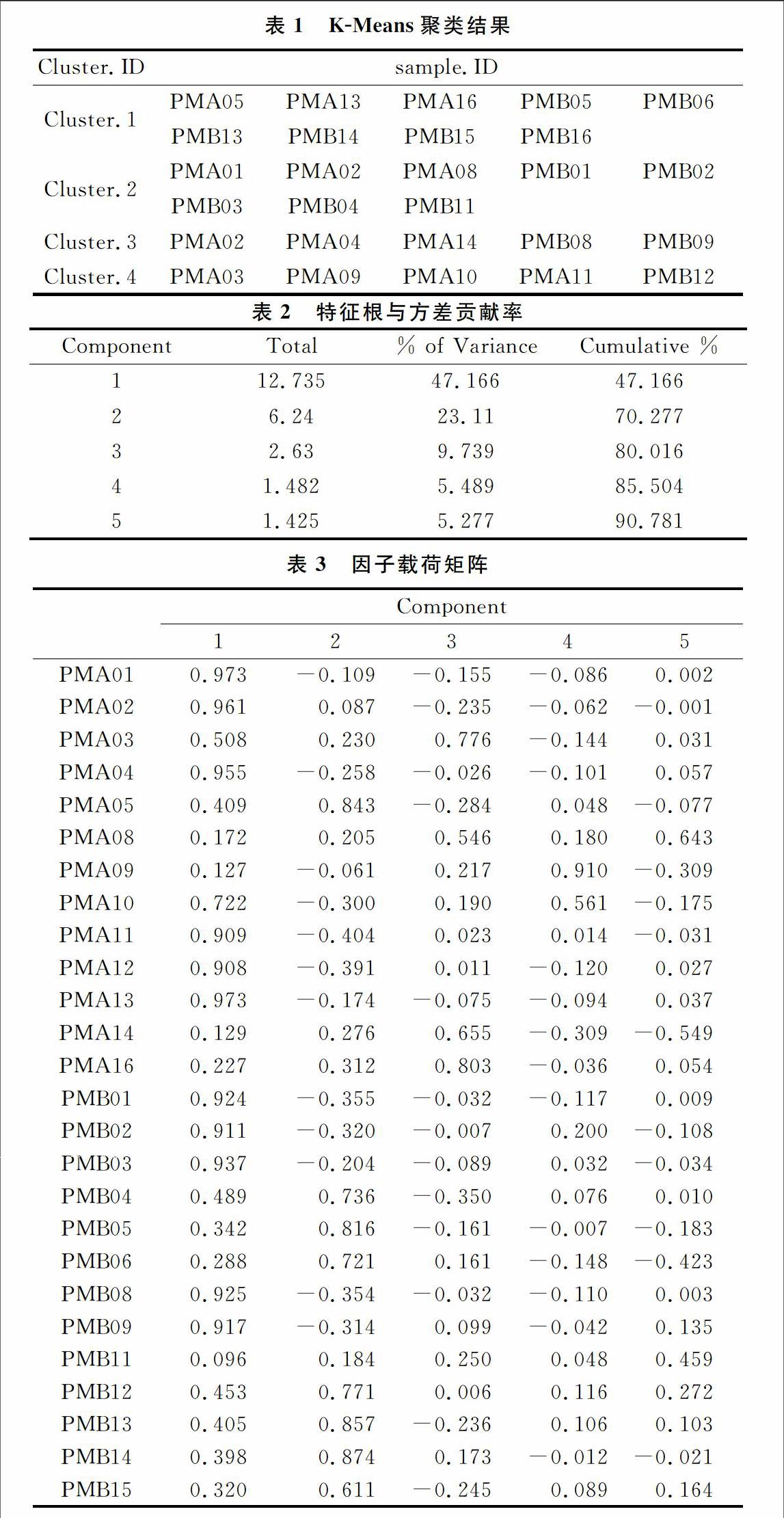
由图1可以看出,样本PMA05、PMB05、PMB13对第1个分类影响最大;PMA01、PMB08对第2个分类影响最大;PMA12、PMA14对第3个分类影响最大;PMA09-11对第4个分类影响最大。表1展示了K-Means的详细聚类结果。
2.2PCA-主成分分析法
以OTUs数据集为评价单元,对其指标数据进行标准化处理后作为样本,利用SPSS 23.0对其进行主成分分析。按照成分因子达到80%~85%即可提取为主成分因子的原则,提取前5个因子作为主成分因子(见表2)。
主成分分析法提取的公共因子,每一载荷量表示主成分与对应变量的相关系数(见表3)。由表3可以看出,公共因子1载荷量较大的样本是PMA01-02、PMA04、PMA11-13、PMB01-02、PMB08-09、PMB16;公共因子2载荷量较大的样本是PMA05、PMB04-06、PMB12-15;公共因子3载荷量较大的样本是PMA03、PMA14、PMA16;公共因子4载荷量较大的样本是PMA09;公共因子5载荷量较大的样本是PMA08。
计算OTU数据集各样本综合得分(见图 2)。
2.3NPTM-pH值
NPTM-pH值是所在样本的pH值,如图3所示。
根据pH值的相似性将OTUs数据集分为4类,分别用4种不同颜色表示。由图3可以看出,K-Means聚类的分类结果与样本pH值的相似性保持一致。
3结语
本文基于K-Means聚类对微生物群落结构进行了研究,K-Means聚类将OTUs数据集的27个样本分成4个Cluster,PCA主成分分析将该样本分成5个Cluster。结合样本元数据,发现K-Means聚类的分析结果能更好地与pH值的相似性保持一致,说明K-Means聚类更能精确地对OTUs数据集进行分类。两种方法评价结果的差异主要与两种方法所确定的权重差异、结果数据处理差异、方法理论差异等有关,同时与标准化处理方法的差异也有一定关系。但综合考虑来看,K-Means聚类相对于PCA方法更能有效地区分微生物群落结构样本。
参考文献:
[1]HUMAN MICROBIOME PROJECT C. Structure, function and diversity of the healthy human microbiome[J]. Nature,2016,486:207-214.
[2]HUMAN MICROBIOME PROJECT C. A framework for human microbiome research[J]. Nature,2016,486:215-221.
[3]曹鹏,贺纪正.微生物生态学理论框架[J].生态学报,2015(22):7263-7273.
[4]车玉伶,王慧,胡洪营,等.微生物群落结构和多样性解析技术研究进展[J].生态环境,2005(1):127-133.
[5]孙志滨.LDA模型的研究及其在推荐系统中的应用[D].杭州:浙江大学,2016.
[6]盛华芳.基于BIPES分析微生物群落的生物信息学方法的建立[D].广州:南方医科大学,2012.
[7]CHENG FAN LI, YANG YANG DAI,JUN JUAN ZHAO, et al. Remote sensing monitoring of volcanic Ash clouds based on PCA metho[J]. Acta Geophysica,2015,63(2):1-19.
[8]POTEMRA T A. The empirical connection of riometer absorption to solar protons during PCA events[J]. Radio Science,2016,7(5):571-577.
[9]Anna Kijewska,Anna Bluszcz. Research of varying levels of greenhouse gas emissions in European countries using the K-Means method[J]. Atmospheric Pollution Research,2016.
[10]TAKASHI ONODA,MIHO SAKAI,SEIJI YAMADA. Careful seeding method based on independent components analysis for K-Means clustering[J]. Journal of Emerging Technologies in Web Intelligence,2012,4(1):112-115.
[11]ZHU L, LEI AH, ZHENG HY, et al. Longitudinal analysis reveals characteristically high proportions of bacterial vaginosis-associated bacteria and temporal variability of vaginal microbiota in northern pig-tailed macaques (Macaca leonina)[J]. Zoological Research,2015,36(5):285-98.
[12]VINCENT COHENADDAD, PHILIP N KLEIN, CLAIRE MATHIEU. Local search yields approximation schemes for K-Means and k-median in Euclidean and minor-free metrics[J]. Foundations of Computer Science,2016:353-364.
[13]SHAHRIVARI S, JALILI S. Single-pass and linear-time K-Means clustering based on MapReduce[J]. Information Systems,2016,60(C):1-12.
[14]COHENADDAD V, KLEIN P N, MATHIEU C. Local search yields approximation schemes for K-Means and K-Median in euclidean and minor-free metrics[C].Foundations of Computer Science,2016:353-364.
[15]SHI Z, SONG W, TAHERI S. Improved LMD, permutation entropy and optimized K-Means to fault diagnosis for roller bearings[J]. Entropy,2016,18(3):70.
[16]HAMIDA E B, JAVED M A. Channel-aware ECDSA signature verification of basic safety messages with K-Means clustering in VANETs[C].IEEE, International Conference on Advanced Information Networking and Applications. IEEE,2016:603-610.
[17]AHMADIAN S, NOROUZI-FARD A, SVENSSON O, et al. Better guarantees for K-Means and euclidean K-Median by primal-dual algorithms[J]. Sciencewise,2016.
(責任编辑:黄健)



摘要:
随着宏基因组学的不断发展,揭示了微生物菌群在研究中的重要作用。采用K-Means聚类算法对来源于北平顶猴阴道微生物群落OTUs数据集的27个样本进行研究,并与PCA主成分分析法进行对比。K-Means聚类将OTUs数据集分成4个Cluster,而PCA将OTUs数据集划分成5个Cluster。此外,结合样本的元数据-pH,发现样本间的pH值相似性更能与K-Means聚类的分类保持一致。相较于PCA主成分析方法,K-Means聚类能更精确地对OTUs数据集进行分类。
关键词:
K-Means聚类;PCA主成分分析法;微生物群落结构;OTUs数据集
DOIDOI:10.11907/rjdk.172732
中图分类号:TP319
文献标识码:A文章编号文章编号:1672-7800(2018)001-0146-03
Abstract:The development of macrogeome has shown that microbial flora plays an important role in the research and development of many aspects. A total of 27 samples from the OTUs data collection of the microbiological community of the North Mongolian monkey were studied by K-Means clustering algorithm and compared with the PCA principal component analysis method. K-Means clustering divides the OTUs data set into four clusters. Interestingly, PCA divides the OTUs data set into five clusters. In addition, combining the sample metadata-pH, it is found that the pH similarity between the samples is more consistent with the classification of K-Means clustering.K-Means clustering classifies the OTUs data sets more accurately than the PCA principal analysis method.
Key Words:K-Means clustering; principal component analysis; microbial community structure; OTUs data set
0引言
微生物群落的种群多样性一直是微生物生态学和环境学科研究的重点。近年来,微生物群落结构成为了研究热点。群落结构决定了生态功能的特性和强弱,因此群落结构的高稳定性是实现生态功能的重要因素,群落结构变化也是标记环境变化的重要指标[1-4]。通过对目标微生物的群落结构和多样性进行解析并研究其动态变化,可为挖掘群落功能信息、优化群落结构与调节群落功能提供可靠依据。
自新一代高通量测序技术2005年问世以来,以其数字化信號、高数据通量、高准确率以及信息量丰富等优点,被广泛应用于微生物菌群研究中[3-6]。本次研究的菌群数据集具有OTUs(Operational Taxonomic Unit)数量多、数据量大、样本信息复杂以及具有一定稀疏性等特点,且微生物群落数据特性与文本分析的变化模式类似。因此,本文提出一种非监督学习算法K-Means聚类算法对微生物群落进行研究。
目前,在微生物群落研究中,PCA主成分分析法也是一种常用方法。PCA 主成分分析法是把多指标转化为少数几个综合指标,使其尽可能多地保留原始变量信息,且彼此不相关[7-8]。但处理结果具有一定模糊性,不能很好地抓住数据的真实子空间结构,当遮挡幅值较大时,效果较差。而K-Means聚类算法是一种非监督学习的硬聚类算法[9],是典型的基于原型的目标函数聚类方法的代表。它是以数据点到原型的某种距离作为优化的目标函数,利用函数求极值的方法得到迭代运算的调整规则,主要采用误差平方和准则函数作为聚类准则函数,以欧式距离作为相似度测度,具有计算速度快、操作简单、时间复杂度近似线性的特点,适合挖掘大规模数据集,且对大数据集分析有较高效率以及可伸缩性[10]。因此,本文采用K-Means聚类分析不同来源或不同时期的微生物群落,并与PCA方法进行对比,使该方法能够进一步运用于微生物研究。
1材料与方法
1.1数据来源
本次数据集来源于两个成年雌性北平顶猴个体PMA和PMB的阴道菌群数据,共27个样本。其中,PMA含有13个时间点数据,PMB含有14个时间点数据[11]。
1.2K-Means聚类原理
K-Means聚类[12-13]也称为K-平均或K-均值,是一种使用最广泛的聚类算法。它是将各个聚类子集内的所有数据样本均值作为该聚类的代表点,算法的主要思想是通过迭代过程把数据集划分为不同类别,使评价聚类性能的准则函数达到最优,从而使生成的每个聚类类内紧凑,类间独立。划分聚类方法对数据集进行聚类时包括如下3个要点:
(1)选定某种距离作为数据样本间的相似性度量。由于K-Means聚类算法不适合处理离散型属性,而对于连续型属性比较适合。因此,在计算数据样本之间的距离时,可以根据实际需要选择欧式距离、曼哈顿距离或者明考斯距离中的一种作为算法的相似性度量[14],其中最常用的是欧式距离。
(3)根據一个簇中对象的平均值进行相似度计算,步骤为:①将所有对象随机分配到k个非空的簇中;②然后计算每个簇的平均值,并用该平均值代表相应的簇;③根据每个对象与各个簇中心的距离,分配给最近的簇;④最后转到②,重新计算每个簇的平均值。该过程不断重复,直到满足某个准则函数才停止。
K-Means聚类的具体算法步骤[17]为:①为每个聚类确定一个初始聚类中心,共有k个初始聚类中心;②将样本集中的样本按照最小距离原则分配到最邻近聚类;③使用每个聚类中的样本均值作为新的聚类中心;④重复步骤②、③,直到聚类中心不再变化;⑤结束,得到k个聚类。
2分析结果
2.1K-Means聚类结果
利用K-Means聚类对北平顶猴OTUs数据集的27个样本进行分析,并通过MEV软件进行计算处理,最终将OTUs数据集分成了4类(见图1)。图1(a)、(b)、(c)、(d)分别表示K-Means聚类的4个Cluster。每行表示每个OTUs在不同样本中的相对丰度,每列表示每个样本中OTUs的相对丰度。
由图1可以看出,样本PMA05、PMB05、PMB13对第1个分类影响最大;PMA01、PMB08对第2个分类影响最大;PMA12、PMA14对第3个分类影响最大;PMA09-11对第4个分类影响最大。表1展示了K-Means的详细聚类结果。
2.2PCA-主成分分析法
以OTUs数据集为评价单元,对其指标数据进行标准化处理后作为样本,利用SPSS 23.0对其进行主成分分析。按照成分因子达到80%~85%即可提取为主成分因子的原则,提取前5个因子作为主成分因子(见表2)。
主成分分析法提取的公共因子,每一载荷量表示主成分与对应变量的相关系数(见表3)。由表3可以看出,公共因子1载荷量较大的样本是PMA01-02、PMA04、PMA11-13、PMB01-02、PMB08-09、PMB16;公共因子2载荷量较大的样本是PMA05、PMB04-06、PMB12-15;公共因子3载荷量较大的样本是PMA03、PMA14、PMA16;公共因子4载荷量较大的样本是PMA09;公共因子5载荷量较大的样本是PMA08。
计算OTU数据集各样本综合得分(见图 2)。
2.3NPTM-pH值
NPTM-pH值是所在样本的pH值,如图3所示。
根据pH值的相似性将OTUs数据集分为4类,分别用4种不同颜色表示。由图3可以看出,K-Means聚类的分类结果与样本pH值的相似性保持一致。
3结语
本文基于K-Means聚类对微生物群落结构进行了研究,K-Means聚类将OTUs数据集的27个样本分成4个Cluster,PCA主成分分析将该样本分成5个Cluster。结合样本元数据,发现K-Means聚类的分析结果能更好地与pH值的相似性保持一致,说明K-Means聚类更能精确地对OTUs数据集进行分类。两种方法评价结果的差异主要与两种方法所确定的权重差异、结果数据处理差异、方法理论差异等有关,同时与标准化处理方法的差异也有一定关系。但综合考虑来看,K-Means聚类相对于PCA方法更能有效地区分微生物群落结构样本。
参考文献:
[1]HUMAN MICROBIOME PROJECT C. Structure, function and diversity of the healthy human microbiome[J]. Nature,2016,486:207-214.
[2]HUMAN MICROBIOME PROJECT C. A framework for human microbiome research[J]. Nature,2016,486:215-221.
[3]曹鹏,贺纪正.微生物生态学理论框架[J].生态学报,2015(22):7263-7273.
[4]车玉伶,王慧,胡洪营,等.微生物群落结构和多样性解析技术研究进展[J].生态环境,2005(1):127-133.
[5]孙志滨.LDA模型的研究及其在推荐系统中的应用[D].杭州:浙江大学,2016.
[6]盛华芳.基于BIPES分析微生物群落的生物信息学方法的建立[D].广州:南方医科大学,2012.
[7]CHENG FAN LI, YANG YANG DAI,JUN JUAN ZHAO, et al. Remote sensing monitoring of volcanic Ash clouds based on PCA metho[J]. Acta Geophysica,2015,63(2):1-19.
[8]POTEMRA T A. The empirical connection of riometer absorption to solar protons during PCA events[J]. Radio Science,2016,7(5):571-577.
[9]Anna Kijewska,Anna Bluszcz. Research of varying levels of greenhouse gas emissions in European countries using the K-Means method[J]. Atmospheric Pollution Research,2016.
[10]TAKASHI ONODA,MIHO SAKAI,SEIJI YAMADA. Careful seeding method based on independent components analysis for K-Means clustering[J]. Journal of Emerging Technologies in Web Intelligence,2012,4(1):112-115.
[11]ZHU L, LEI AH, ZHENG HY, et al. Longitudinal analysis reveals characteristically high proportions of bacterial vaginosis-associated bacteria and temporal variability of vaginal microbiota in northern pig-tailed macaques (Macaca leonina)[J]. Zoological Research,2015,36(5):285-98.
[12]VINCENT COHENADDAD, PHILIP N KLEIN, CLAIRE MATHIEU. Local search yields approximation schemes for K-Means and k-median in Euclidean and minor-free metrics[J]. Foundations of Computer Science,2016:353-364.
[13]SHAHRIVARI S, JALILI S. Single-pass and linear-time K-Means clustering based on MapReduce[J]. Information Systems,2016,60(C):1-12.
[14]COHENADDAD V, KLEIN P N, MATHIEU C. Local search yields approximation schemes for K-Means and K-Median in euclidean and minor-free metrics[C].Foundations of Computer Science,2016:353-364.
[15]SHI Z, SONG W, TAHERI S. Improved LMD, permutation entropy and optimized K-Means to fault diagnosis for roller bearings[J]. Entropy,2016,18(3):70.
[16]HAMIDA E B, JAVED M A. Channel-aware ECDSA signature verification of basic safety messages with K-Means clustering in VANETs[C].IEEE, International Conference on Advanced Information Networking and Applications. IEEE,2016:603-610.
[17]AHMADIAN S, NOROUZI-FARD A, SVENSSON O, et al. Better guarantees for K-Means and euclidean K-Median by primal-dual algorithms[J]. Sciencewise,2016.
(責任编辑:黄健)

