陶瓷大板双摆动式抛光加工工艺研究
徐斌
摘 要:针对现有陶瓷大板表面加工不均匀、漏抛问题,本文提出了陶瓷大板双摆动式抛光加工工艺,建立了横梁纵横向摆动数学模型,建立了同频率以及频率比值为2:1,3:1,1:2,1:3,3:2,2:3时,相位为0、π/4、π/2,不同摆动幅度下的合成运动轨迹,建立了该合成运动轨迹与陶瓷大板直线进给运动的合成加工轨迹。研究结果得出:同频率时,合成轨迹多是圆形和椭圆形;不同频率时,合成轨迹是李萨如图形。同频率时,合成加工轨迹多是长摆线,不同频率时,合成轨加工迹是多变的图形。心形轨迹不适合陶瓷大板加工,长摆线轨迹和8字形轨迹、上下8字形轨迹是最优的加工轨迹。同时给出了最优加工轨迹的加工工艺参数。
关键词:陶瓷大板;双摆动;长摆线;8字形;李萨如图形
1 前言
陶瓷大板目前在国内外市场炙手可热[1],当前的陶瓷大板还是沿用传动的摆动式抛光加工工艺,仅仅是将传统摆动式抛光机的宽度加大。当传统摆动式抛光机的宽度加大以后,就会出现一系列的问题[2、3],如:摆动频率与瓷砖进给之间的匹配关系,陶瓷大板的漏抛、表面磨削均匀性差等问题。
石材大板与陶瓷大板在加工工艺上有相似之处,因此石材大板的加工工艺对陶瓷大板的深加工具有借鉴意义。到目前为止,国内外最新石材大板的加工工艺有如下几种:圆形轨迹加工工艺、双摆动式加工工艺、单摆动式加工工艺。2018年厦门国际石材及其加工装备展会上,百利通、西斯特姆、萨克米等国外知名公司,均展出了石材双摆动式加工工艺。这种加工工艺仅仅在国外应用,在国内却未见厂家使用。这种工艺早在2015年意大利展会上就展出过,国内企业却没有跟风、也没有借鉴。原因如下:运动复杂、石材表面复合运动轨迹多变,没有基础理论研究做支撑,运动轨迹没有数学模型、工艺参数没有理论数据。再加上国外的技术封锁,这些因素制约了双摆动式抛光工艺在石材大板上的应用和推广。
本文提出了陶瓷大板双摆动式抛光加工工艺,建立横梁双摆动数学模型、及双摆动合成运动轨迹。建立横梁双摆动在陶瓷大板表面复合加工轨迹。给出最优化的复合加工轨迹的工艺参数。研究结果为双摆动式抛光机的设计提供理论基础、打破国外技术封锁,在国内陶瓷和石材行业的推广及应用提供理论基础。
2 陶瓷大板双摆动式抛光加工工艺原理
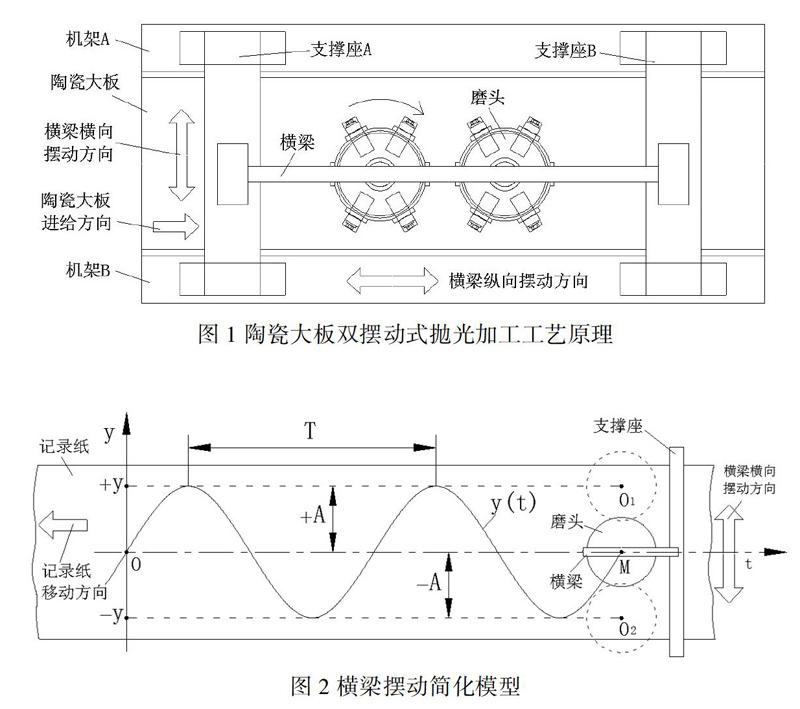
图1为陶瓷大板双摆动式抛光加工工艺原理图,陶瓷大板双摆动式抛光机有三种主要的运动:第一种是横梁的横向往复摆动,磨头安装在横梁上,横梁支撑在支撑座A、B上。横梁及其安装在其上的磨头,在电机的驱动下,在支撑座A、B上来回的作横向摆动。第二种是横梁的纵向往复摆动,支撑座A、B安装在机架A、B上,在电机的驱动下支撑座A、B,以及安装其上的横梁和磨头作纵向往复摆动。所谓的双摆动就是横梁作横向往复摆动的同时也作纵向摆动。第三种是陶瓷大板的直线进给运动,磨头在陶瓷大板表面的加工轨迹是横梁的横向、纵向的双摆动与陶瓷大板的直线运动三种运动复合的结果。由于结构设计的不同,很多时候,也可以是横梁在支撑座A、B上即作横向摆动,也作纵向摆动。而支撑座固定在机架上不动。
3 横梁纵横摆动的数学模型
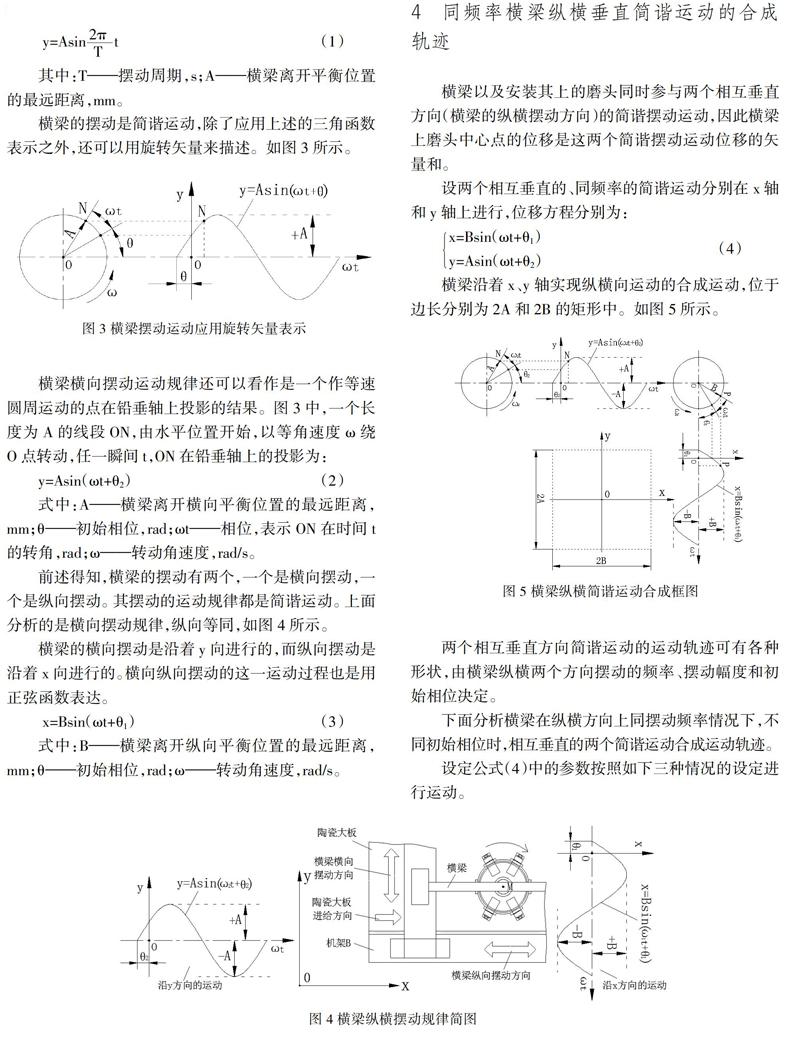
下面将横梁的摆动进行简化,建立其数学模型。磨头安装在横梁之上,磨头的中心点位置在M点。在此取横梁支撑座的中心位置作为横梁摆动的静态平衡位置。如图2所示。取横梁支撑座的中点为位置作为坐标原点O,在图中所示,横梁是沿着上下方向摆动的,沿着运动方向取坐标y(向上为正)。磨头中点M的任意一点位置可有横梁的y坐标确定。
横梁的一个周期的横向摆动过程如下:横梁从静态平衡位置O开始,也就是横梁支撑座的中心位置开始。先是向上摆动,磨头中心点M摆动到上极限位置O1,接着从O1点开始返回向下摆动,通过横梁支撑座的中心位置之后,继续向下摆动,磨头中心点M摆动到下极限位置O2,接着从O2点开始返回向上摆动,到达横梁支撑座的中心位置O。横梁的一个周期的横向摆动结束。周而复始。
如图2所示,从横梁的横向摆动规律来看,其运动规律为简谐运动。接下来,本文采用模拟的方法展示横梁简谐运动的特性。横梁是按照前述的运动的规律开始运动,若在磨头中心点M的位置上放置一个小光源,使它的一束光照射在一条匀速水平移动的光敏纸带上,记录下横梁横向摆动的运动量随着时间的变化规律,横梁位移的时间历程是时间t的正弦函数,因此,横梁横向摆动这一运动过程可用下面正弦函数表达。
4 同频率横梁纵横垂直简谐运动的合成轨迹
横梁以及安装其上的磨头同时参与两个相互垂直方向(横梁的纵横摆动方向)的简谐摆动运动,因此横梁上磨头中心点的位移是这两个简谐摆动运动位移的矢量和。
设两个相互垂直的、同頻率的简谐运动分别在x轴和y轴上进行,位移方程分别为:
横梁沿着x、y轴实现纵横向运动的合成运动,位于边长分别为2A和2B的矩形中。如图5所示。
两个相互垂直方向简谐运动的运动轨迹可有各种形状,由横梁纵横两个方向摆动的频率、摆动幅度和初始相位决定。
下面分析横梁在纵横方向上同摆动频率情况下,不同初始相位时,相互垂直的两个简谐运动合成运动轨迹。
设定公式(4)中的参数按照如下三种情况的设定进行运动。
横梁纵横方向摆动的简谐运动规律,在此用旋转矢量表示。ω1、ω2旋转矢量的转动频率,转动的方向是相同的,矢量圆的半径A、B分别是横梁离开纵横向平衡位置的最远距离。旋转矢量的起始位置按照三种条件的初始相位设置进行。
合成运动的绘制方法如下:
将表示旋转矢量的圆周进行等分,等分的分数随意确定,本文等分为8等分,按照旋转矢量的旋转方向,从0开始标注标号,如6图所示。纵横方向的矢量圆的起始位置,用箭头表示。
依次从零点开始,横向矢量圆的0点位置引出直线至合成区域,纵向矢量圆的0点位置引出直线至合成区域,引出线在图中用虚线表示。纵横向0点位置的引出线相较于合成区域。相交点就是纵横运动的合成点,标注为0。按照同样的方向,参照纵横矢量的旋转的方向,依次再从1点引线至合成区域,相交点为合成运动的1点。依次类推,至8点结束。将合成区域的点,依次连接成曲线,就是在纵横相互垂直运动下,在给出的相位条件下的合成运动轨迹曲线。
5 同频率横梁纵横垂直简谐运动与陶瓷大板直线运动,在陶瓷大板表面合成的综合运动轨迹
上述的分析是在没有考虑陶瓷大板直线运动的情况下,单纯横梁纵横向相互垂直简谐运动的合成运动轨迹。在实际过程中,磨头是安装在横梁上,横梁的合成运动轨迹,也是磨头中心点的运动轨迹。磨头与陶瓷大板表面接触,研抛陶瓷大板的表面,因此,磨头在陶瓷大板表面的加工轨迹,是横梁纵横向垂直简谐运动的合成运动与陶瓷大板直线运动的再次合成。运动轨迹合成结果如图7所示。
图7对应着图6,例如图7(a)是图6(a)与陶瓷大板直线运动合成的结果,是横梁纵横向垂直简谐运动时,矢量圆旋转一周,陶瓷大板在移动的距离,纵横向垂直简谐运动与陶瓷大板直线运动在其表面合成的运动轨迹。
图7可看出:
(1)横梁纵横向简谐运动合成运动为一条斜直线时,磨头在陶瓷大板表面上的合成加工轨迹为倾斜的之字形长波。
(2)横梁纵横向简谐运动合成运动为斜椭圆、正圆、纵、横向正椭圆时,磨头在陶瓷大板表面上的合成加工轨迹都是长摆线轨迹。只不过是摆线轨迹有倾斜、正向、长短之分。
同频率时,纵横向垂直简谐运动与陶瓷大板直线运动在其表面合成的连续运动轨迹,如图8所示。图8对应着图7,如图8(a)对应着图7(a)。
6 不同頻率横梁纵横垂直简谐运动的合成轨迹
当横梁纵横垂直的简谐运动的频率不相等时,它们的合成运动就更加复杂, 相互垂直的两个简谐运动的频率相差很大,但是有简单的整数比值时,则合成运动具有稳定的封闭运动轨迹。这种频率成简单整数比时,所得到的稳定的合成轨迹线称为李萨如图形。
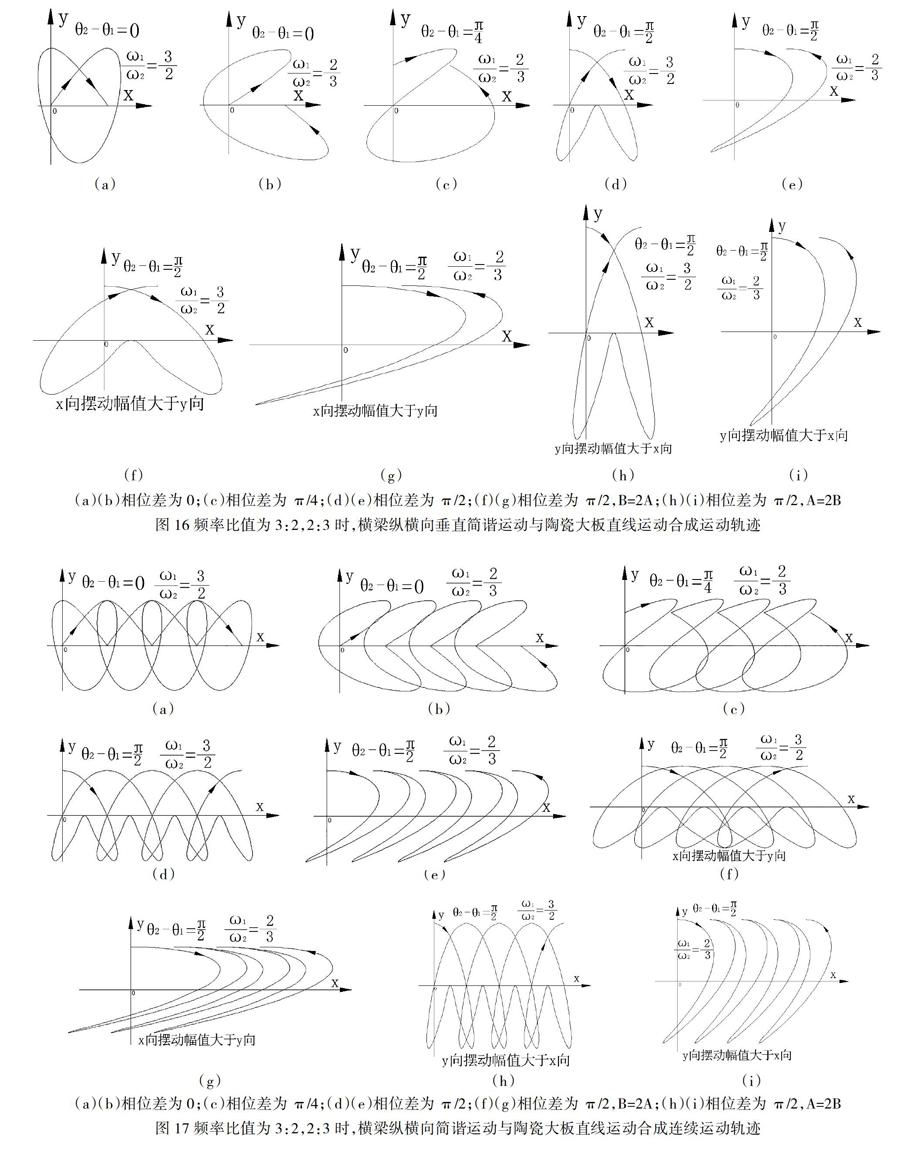
频率比值为3:2,2:3时,纵横向垂直简谐运动与陶瓷大板直线运动在其表面合成的运动轨迹,如图16所示。图16对应着图15,如图16(a)对应着图15(a)。
频率比值为3:2,2:3时,纵横向垂直简谐运动与陶瓷大板直线运动在其表面合成的连续运动轨迹,如图17所示。图17对应着图16,如图17(a)对应着图16(a)。
图15、16、17显示,频率比值为3:2,2:3时,横梁纵横向简谐运动合成轨迹是一个心形,这种轨迹会在陶瓷大板的边缘处残留很大的一个空白区域,会产生漏抛,以及抛光不均匀。



摘 要:针对现有陶瓷大板表面加工不均匀、漏抛问题,本文提出了陶瓷大板双摆动式抛光加工工艺,建立了横梁纵横向摆动数学模型,建立了同频率以及频率比值为2:1,3:1,1:2,1:3,3:2,2:3时,相位为0、π/4、π/2,不同摆动幅度下的合成运动轨迹,建立了该合成运动轨迹与陶瓷大板直线进给运动的合成加工轨迹。研究结果得出:同频率时,合成轨迹多是圆形和椭圆形;不同频率时,合成轨迹是李萨如图形。同频率时,合成加工轨迹多是长摆线,不同频率时,合成轨加工迹是多变的图形。心形轨迹不适合陶瓷大板加工,长摆线轨迹和8字形轨迹、上下8字形轨迹是最优的加工轨迹。同时给出了最优加工轨迹的加工工艺参数。
关键词:陶瓷大板;双摆动;长摆线;8字形;李萨如图形
1 前言
陶瓷大板目前在国内外市场炙手可热[1],当前的陶瓷大板还是沿用传动的摆动式抛光加工工艺,仅仅是将传统摆动式抛光机的宽度加大。当传统摆动式抛光机的宽度加大以后,就会出现一系列的问题[2、3],如:摆动频率与瓷砖进给之间的匹配关系,陶瓷大板的漏抛、表面磨削均匀性差等问题。
石材大板与陶瓷大板在加工工艺上有相似之处,因此石材大板的加工工艺对陶瓷大板的深加工具有借鉴意义。到目前为止,国内外最新石材大板的加工工艺有如下几种:圆形轨迹加工工艺、双摆动式加工工艺、单摆动式加工工艺。2018年厦门国际石材及其加工装备展会上,百利通、西斯特姆、萨克米等国外知名公司,均展出了石材双摆动式加工工艺。这种加工工艺仅仅在国外应用,在国内却未见厂家使用。这种工艺早在2015年意大利展会上就展出过,国内企业却没有跟风、也没有借鉴。原因如下:运动复杂、石材表面复合运动轨迹多变,没有基础理论研究做支撑,运动轨迹没有数学模型、工艺参数没有理论数据。再加上国外的技术封锁,这些因素制约了双摆动式抛光工艺在石材大板上的应用和推广。
本文提出了陶瓷大板双摆动式抛光加工工艺,建立横梁双摆动数学模型、及双摆动合成运动轨迹。建立横梁双摆动在陶瓷大板表面复合加工轨迹。给出最优化的复合加工轨迹的工艺参数。研究结果为双摆动式抛光机的设计提供理论基础、打破国外技术封锁,在国内陶瓷和石材行业的推广及应用提供理论基础。
2 陶瓷大板双摆动式抛光加工工艺原理
图1为陶瓷大板双摆动式抛光加工工艺原理图,陶瓷大板双摆动式抛光机有三种主要的运动:第一种是横梁的横向往复摆动,磨头安装在横梁上,横梁支撑在支撑座A、B上。横梁及其安装在其上的磨头,在电机的驱动下,在支撑座A、B上来回的作横向摆动。第二种是横梁的纵向往复摆动,支撑座A、B安装在机架A、B上,在电机的驱动下支撑座A、B,以及安装其上的横梁和磨头作纵向往复摆动。所谓的双摆动就是横梁作横向往复摆动的同时也作纵向摆动。第三种是陶瓷大板的直线进给运动,磨头在陶瓷大板表面的加工轨迹是横梁的横向、纵向的双摆动与陶瓷大板的直线运动三种运动复合的结果。由于结构设计的不同,很多时候,也可以是横梁在支撑座A、B上即作横向摆动,也作纵向摆动。而支撑座固定在机架上不动。
3 横梁纵横摆动的数学模型
下面将横梁的摆动进行简化,建立其数学模型。磨头安装在横梁之上,磨头的中心点位置在M点。在此取横梁支撑座的中心位置作为横梁摆动的静态平衡位置。如图2所示。取横梁支撑座的中点为位置作为坐标原点O,在图中所示,横梁是沿着上下方向摆动的,沿着运动方向取坐标y(向上为正)。磨头中点M的任意一点位置可有横梁的y坐标确定。
横梁的一个周期的横向摆动过程如下:横梁从静态平衡位置O开始,也就是横梁支撑座的中心位置开始。先是向上摆动,磨头中心点M摆动到上极限位置O1,接着从O1点开始返回向下摆动,通过横梁支撑座的中心位置之后,继续向下摆动,磨头中心点M摆动到下极限位置O2,接着从O2点开始返回向上摆动,到达横梁支撑座的中心位置O。横梁的一个周期的横向摆动结束。周而复始。
如图2所示,从横梁的横向摆动规律来看,其运动规律为简谐运动。接下来,本文采用模拟的方法展示横梁简谐运动的特性。横梁是按照前述的运动的规律开始运动,若在磨头中心点M的位置上放置一个小光源,使它的一束光照射在一条匀速水平移动的光敏纸带上,记录下横梁横向摆动的运动量随着时间的变化规律,横梁位移的时间历程是时间t的正弦函数,因此,横梁横向摆动这一运动过程可用下面正弦函数表达。
4 同频率横梁纵横垂直简谐运动的合成轨迹
横梁以及安装其上的磨头同时参与两个相互垂直方向(横梁的纵横摆动方向)的简谐摆动运动,因此横梁上磨头中心点的位移是这两个简谐摆动运动位移的矢量和。
设两个相互垂直的、同頻率的简谐运动分别在x轴和y轴上进行,位移方程分别为:
横梁沿着x、y轴实现纵横向运动的合成运动,位于边长分别为2A和2B的矩形中。如图5所示。
两个相互垂直方向简谐运动的运动轨迹可有各种形状,由横梁纵横两个方向摆动的频率、摆动幅度和初始相位决定。
下面分析横梁在纵横方向上同摆动频率情况下,不同初始相位时,相互垂直的两个简谐运动合成运动轨迹。
设定公式(4)中的参数按照如下三种情况的设定进行运动。
横梁纵横方向摆动的简谐运动规律,在此用旋转矢量表示。ω1、ω2旋转矢量的转动频率,转动的方向是相同的,矢量圆的半径A、B分别是横梁离开纵横向平衡位置的最远距离。旋转矢量的起始位置按照三种条件的初始相位设置进行。
合成运动的绘制方法如下:
将表示旋转矢量的圆周进行等分,等分的分数随意确定,本文等分为8等分,按照旋转矢量的旋转方向,从0开始标注标号,如6图所示。纵横方向的矢量圆的起始位置,用箭头表示。
依次从零点开始,横向矢量圆的0点位置引出直线至合成区域,纵向矢量圆的0点位置引出直线至合成区域,引出线在图中用虚线表示。纵横向0点位置的引出线相较于合成区域。相交点就是纵横运动的合成点,标注为0。按照同样的方向,参照纵横矢量的旋转的方向,依次再从1点引线至合成区域,相交点为合成运动的1点。依次类推,至8点结束。将合成区域的点,依次连接成曲线,就是在纵横相互垂直运动下,在给出的相位条件下的合成运动轨迹曲线。
5 同频率横梁纵横垂直简谐运动与陶瓷大板直线运动,在陶瓷大板表面合成的综合运动轨迹
上述的分析是在没有考虑陶瓷大板直线运动的情况下,单纯横梁纵横向相互垂直简谐运动的合成运动轨迹。在实际过程中,磨头是安装在横梁上,横梁的合成运动轨迹,也是磨头中心点的运动轨迹。磨头与陶瓷大板表面接触,研抛陶瓷大板的表面,因此,磨头在陶瓷大板表面的加工轨迹,是横梁纵横向垂直简谐运动的合成运动与陶瓷大板直线运动的再次合成。运动轨迹合成结果如图7所示。
图7对应着图6,例如图7(a)是图6(a)与陶瓷大板直线运动合成的结果,是横梁纵横向垂直简谐运动时,矢量圆旋转一周,陶瓷大板在移动的距离,纵横向垂直简谐运动与陶瓷大板直线运动在其表面合成的运动轨迹。
图7可看出:
(1)横梁纵横向简谐运动合成运动为一条斜直线时,磨头在陶瓷大板表面上的合成加工轨迹为倾斜的之字形长波。
(2)横梁纵横向简谐运动合成运动为斜椭圆、正圆、纵、横向正椭圆时,磨头在陶瓷大板表面上的合成加工轨迹都是长摆线轨迹。只不过是摆线轨迹有倾斜、正向、长短之分。
同频率时,纵横向垂直简谐运动与陶瓷大板直线运动在其表面合成的连续运动轨迹,如图8所示。图8对应着图7,如图8(a)对应着图7(a)。
6 不同頻率横梁纵横垂直简谐运动的合成轨迹
当横梁纵横垂直的简谐运动的频率不相等时,它们的合成运动就更加复杂, 相互垂直的两个简谐运动的频率相差很大,但是有简单的整数比值时,则合成运动具有稳定的封闭运动轨迹。这种频率成简单整数比时,所得到的稳定的合成轨迹线称为李萨如图形。
频率比值为3:2,2:3时,纵横向垂直简谐运动与陶瓷大板直线运动在其表面合成的运动轨迹,如图16所示。图16对应着图15,如图16(a)对应着图15(a)。
频率比值为3:2,2:3时,纵横向垂直简谐运动与陶瓷大板直线运动在其表面合成的连续运动轨迹,如图17所示。图17对应着图16,如图17(a)对应着图16(a)。
图15、16、17显示,频率比值为3:2,2:3时,横梁纵横向简谐运动合成轨迹是一个心形,这种轨迹会在陶瓷大板的边缘处残留很大的一个空白区域,会产生漏抛,以及抛光不均匀。

