第一视角的强化学习

    陈凯

    如在梦境中一般，他跌跌撞撞行进在幽暗的洞穴迷宫中，他依稀记起自己此行的目标——尽快找到那难以估价的宝藏，并避免遭到巨型蜘蛛的攻击。可是，下一步，是由此通往哪里，而此前，自己又是从哪条路来到此处，他却完全没有了印象，在火把的闪光中，他注意到狭窄通道的墙上留着一些神秘的记号……

    这是一个迷宫寻宝游戏，玩家的目的是找到宝藏，同时避开危险的动物，为了文章描述方便，迷宫的结构设计得很简单，如表1所示。

    迷宫里有11个直接或间接连通的空间，有一些地方被岩石堵住无法通行，开始游戏时，玩家在迷宫的左下角，而宝藏在迷宫的右上角，危险的动物紧挨着宝藏，要是玩家能看到这张迷宫结构图，那游戏未免太简单了，往上走两步，再往右走三步就完成了任务。然而，这是一个第一视角游戏，玩家只能看到自己当前所处空间的状况，而不知道上下左右其他空间的状况，于是为了找到宝藏，就只有随机四处行走来碰运气。还有一个麻烦的问题是，玩家所控制的角色是个失忆症重症患者，每次进入到新的空间，他的记忆就会被清空，就算是最终获得了宝藏或者撞上了危险动物，在回到初始位置重玩游戏时，刚才这种纯粹碰运气式的“努力”也都要全部再来一次。

    但若玩家可以在空间与空间的交界处留下一些特殊的信息，情况就能有所改善，由于每完成一步移动就会失忆，所以玩家不能把整個迷宫的结构图画出来，但至少可以记录一下，自己来到当前空间的这一步行进动作是否划算。

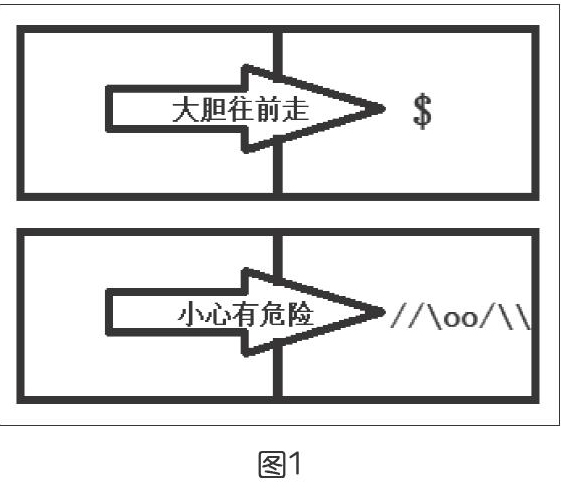
    比如说，若新进入的空间里有宝藏，可以在进入的交界处留下“大胆往前走”的标志;如果新进入的空间里有危险的动物，就在交界处留下“小心有危险”的标志，如图1所示。不过也有这样的情况，新进入的某个空间，称之为当前空间，这里并没有什么东西，但却能看到在当前空间通向下一个空间的交界处留下的标记是“大胆往前走”，那就可以在之前的空间与当前空间的交界处留下一个“值得往前走”的标记，如图2所示。

    

    

    

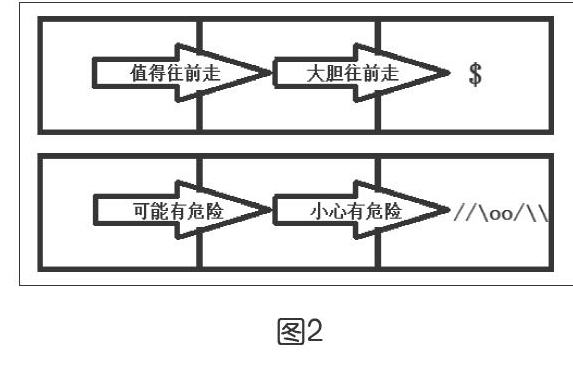
    以此类推，如果发现当前空间通往下一空间的交界处标记有“值得往前走”，那么还可以在之前空间通往当前空间的交界处留下“可以试着走”的标记。可是，为什么不全部标记“大胆往前走”呢？因为在一个复杂的迷宫里，通往宝藏的路径可能不止一条，虽然说在某次探险中标记了一条可以通往宝藏的道路，但有可能这一条完全靠蒙的道路弯弯绕绕，兜了一个不必要的大圈子才到达目的地，所以，只要不是紧挨着宝藏，标记就不能写得很绝对。通过上述这种方法，既可以把远处的状况信息，依靠临近空间的标记逐渐扩散开来，又能提供给探险的玩家多种行进的可能性，这正是Q-learning强化学习的重要思路。那么，这种思路是如何真正落实到人工智能算法的实现中去的？对这个问题的解答，便成为开展教学的主要内容。1.给迷宫编码

    为了处理迷宫中的各种信息，需要将迷宫的结构、迷宫里的东西、在迷宫中行走的动作以及特定动作执行后在空间交界处所留下的标记，都编码成数字或字母。

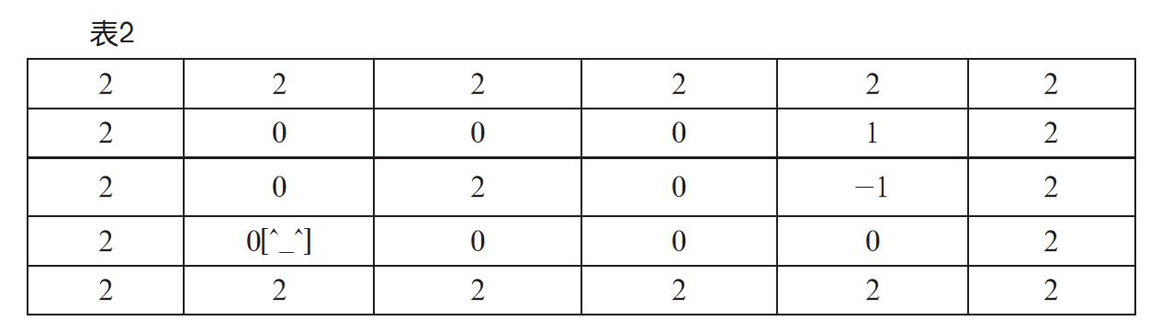
    例如，把可以进入的空无一物的空间标记为0，无法进入的岩石墙体标记为2，有宝藏的空间标记为1，有危险动物的空间标记为-1，于是迷宫成为一个二维数组，如表2所示。

    在游戏中，玩家的角色会变化位置，所以用x和y两个变量来确定玩家当前的位置，整个数组（列表）从下往上数从第0行到第4行共5行，从左往右数从第0列到第5列共6列。因为玩家的角色并不会穿墙术，所以将x和y都设置为1，表示他在最左下角的空间里。将这个空间布局用Python的列表来表示，就如图3所示的样子。

    

    

    

    

    然而还需要另外一张表，来记录空间交界处为每个行进动作所做的策略标记，因为在每个空间中，可能有上下左右四个行进方向，所以就需要用一个三维的数组（列表）来记录数据，如表3所示。

    用Python代码表示就如图4所示。

    可以将这个数组（列表）称为Q表，初始状态下，默认的策略标记都是0。[0，0，0，0]中用逗号隔开的四个部分，分别代表着向右、向下、向左和向上四种不同行进动作的策略值。值越大，就代表这个动作越划算，反之则是不划算。

    接下来，是给上下左右每一步行进动作编码，这里可以用四个字母代表上下左右四个方向，比如，“w”是上，“s”是下，“a”是左，“d”是右，这样编码有个好处，如果在键盘上控制角色的前进方向，也可以用“w”“s”“a”“d”这四个按键。用按键控制玩家的角色上下左右移动，并判定是否获取宝藏或遭遇危险动物的代码非常简单，如图5所示。

    代码中，将角色的y变量加1，等同于往右走;y变量减1，等同于往左走;x变量加1，等同于向上走;x变量减1，等同于向下走。限于篇幅本文没有列出全部代码，但补全代码十分容易，读者也可以自行设法利用函数，使得代码更为简洁。

    

    

    到这里，玩家已经可以控制角色在迷宫中自由探索了，不过到目前为止，还没有解决先前所说的失忆症问题。接下来的任务，是要使前一次通关的经验能够为后一次通关提供帮助，将每一次行进动作的划算程度记录到Q表中。2.充满智慧的数学公式

    相较于用一堆含混不清的文字来标记特定动作的划算程度，直接用一个数字作为动作的策略值，明显更有利于“无脑”的决策。比如，策略值数字大则推荐走，数字小则不推荐，因为游戏初始时，Q表中所有的策略值都是0，所以就需要根據特定行进动作的效果来更改值。

    比如，在游戏初始时，玩家角色可以向上走，也可以向右走，但向左和向下的路是不通的，即便一定要顽固去走，结果只是无端撞墙后回到原地，这时候就可以在Q表中记录一下策略值的变化：q[x][y][2]=q[x][y][2]-0.2。因为游戏初始时x和y是1，所以相当于是：q[1][1][2]=q[1][1][2]-0.2。

    结果，q[1][1][2]的值是-0.2。因为值变小了，表示这个行进方向不太划算。“[1][1][2]”是列表q的三个下标，第一个下标表示角色所处的行，第二个下标表示所处列，第三个下标表示角色的行进动作，“0”“1”“2”“3”分别代表向右、向下、向左、向上四个方向。

    如果角色向右走进入了藏有宝藏的空间，则公式是：q[x][y][0]=q[x][y][0]+0.5。

    为了说明这个动作非常划算，策略值变大了。类似地，如果进入到藏有危险动物的空间，策略值就会变小。

    以上公式都十分容易理解，但在Q-learning强化学习，最有智慧的公式，出现在玩家角色进入到空无一物的空间后，对动作策略所进行的修改。下面的代码是角色向上行进时，Q表中策略值发生的更改：q[x][y][3]=q[x][y][3]+0.1*（-0.1+0.9*max（q[x+1][y][0]，q[x+1][y][1]，q[x+1][y][2]，q[x+1][y][3]）-q[x][y][3]）。

    

    

    将代码分解如下：

    max（q[x+1][y][0]，q[x+1][y][1]，q[x+1][y][2]，q[x+1][y][3]），目的是取得新进入的当前空间通往下一空间交界处各行进策略值中的最大值。

    0.9*max（q[x+1][y][0]，q[x+1][y][1]，q[x+1][y][2]，q[x+1][y][3]），目的是要把这个策略值进行打折处理，0.9就是折扣率，比如说，在紧挨着宝藏的空间中，策略值是“百分百推荐这么走”，离开较远一些，则应该是“比较推荐这么走”。这样才能提供多条路径选择的可能。

    -0.1+0.9*max（q[x+1][y][0]，q[x+1][y][1]，q[x+1][y][2]，q[x+1][y][3]），因为要避免兜圈子多走路，只要是走了一步，那么策略值就要减少一些，所以这里减去0.1。

    0.1*（-0.1+0.9*max（q[x+1][y][0]，q[x+1][y][1]，q[x+1][y][2]，q[x+1][y][3]）-q[x][y][3]），把上述结果乘以学习率0.1，如果学习率设置得太高，结果可能是玩家会被框死在某条未必划算的路径上，如果设置得太低，那么行进动作策略的指示作用就难以体现出来。

    折扣率和学习率的取值大小并没有标准答案，需要不断调整以使得算法获得更优效果，所以，可以在代码起始时使用两个变量代表折扣率和学习率，使得程序调试更为方便，上页图6是实现玩家动作及Q表策略值更新的部分代码，限于篇幅，只提供向右行进并更改Q表策略值的代码，其他几个方向的行进代码其实是类似的。3.一边玩，一边学

    写到这里，笔者准备宣布一个稍微让人沮丧的消息，本文虽然讲了Q-learning强化学习算法的核心思想，也提供了部分实际可以运行的程序代码，但要完整实现Q-learning的算法，还有许多事情要做。比如说，若要让机器代替玩家自动分析数据并进行下一步动作的决策，就需要在代码中增加条件判断;为了让机器能探索更广阔的空间而不局限于先前行动的Q表的决策数据，就要引入随机函数，并需要在纯粹随机的动作和Q表的决策数据之间进行平衡;为了让代码具有更多普适性，还要改造数据结构，引入线性代数中“矩阵”的概念……笔者认为，如果人工智能教学面向的是基础教育领域整体的学习者，在课时和学习者当前知识技能水平受到限制的情况下，教学的重点应该在于促成学习者对机器学习的根本思想方法的领悟，而不在于完整的机器学习算法的代码的构建。

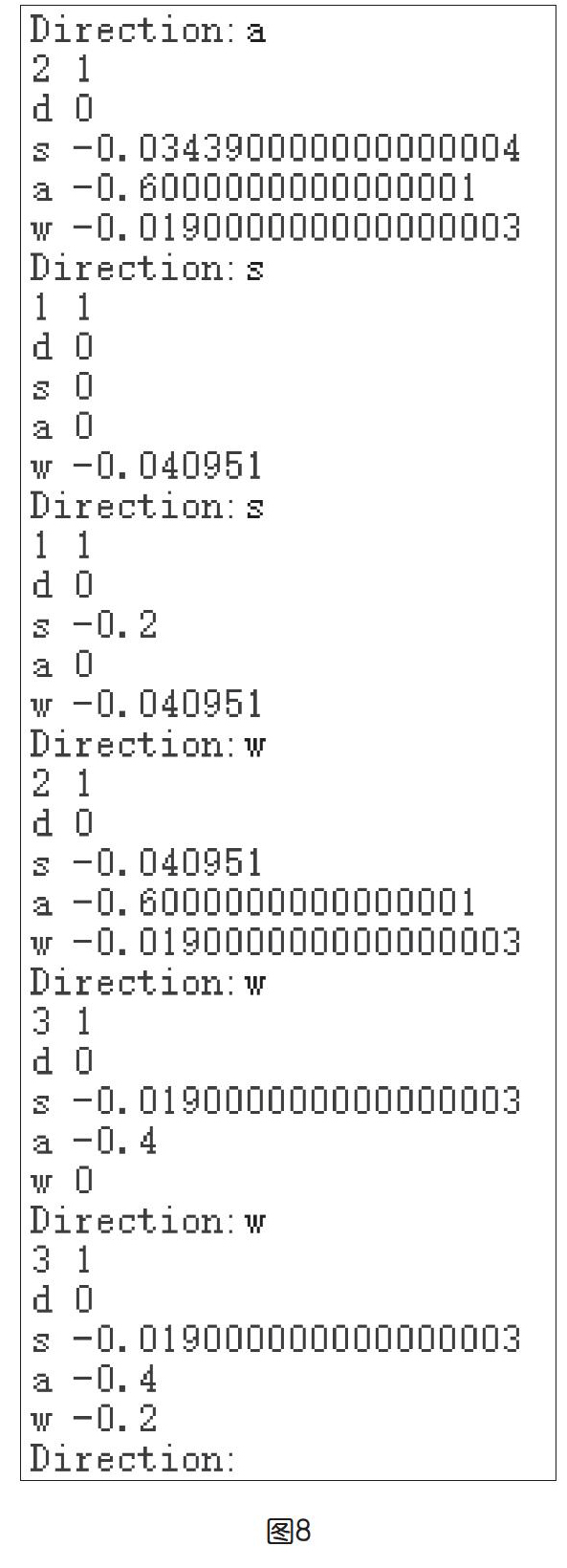
    本文提供的Q-learning强化学习算法的代码虽然并不具有机器智能学习的完整功能，但却提供了第一视角下亲身体验机器学习过程的可能，通俗来说，就是能够很容易玩起来，一边玩，一边思考那些不断变化的策略值的含义。在程序运行之初，界面中毫无有价值的信息，四个方向的空间交界处的数值都是0，玩家也只能随便瞎走，如上页图7所示。但在多次行动后，通往四个方向的空间交界处的数据就有了提示作用，如上页图8所示。

    比如，在最后一行的互动操作，应该选哪个方向行进呢？向右的“d”和向下的“s”所对应的数值都比较大且相差不多，所以可以随便选一个动作试试，人是这样判断的，若是编程让机器做出这样的判断，也并不是什么困难的事情。为了使得“失忆症”效果更强烈，也就是说，让玩家的行为更接近机器学习中机器的行为，还可以进行一些小变化，比如，将程序代码中指示当前空间位置的代码删除掉，或者让两位学生交替输入行进动作的方向，甚至两两组队开展寻宝比赛，看哪一组学生可以在规定时间内更多次获取到宝藏。

    在第一次乃至前几次寻宝过程中，空间交界处的策略值数据差别不是很大，但多次寻宝成功，或者多次遭遇危险动物失败后，这些数值的大小会逐步拉开差距，使得玩家的行进方向越来越明显，这就体现了Q-learning算法延迟获得回报的特征。只要多玩几次游戏，就能领悟为什么延迟回报对类似迷宫探险这样的游戏特别有用，这比多少单纯的口叙笔述都更有效。假想一下，在基础教育领域，面对全体学生讲授Q-learning算法却只有短短40分钟课时，那该怎么安排教学内容呢？笔者会拿出一半的课时来实施寻宝游戏的比赛，读者们又怎么想呢？