基于ANSYS的CSAMT法三维正演仿真模拟基础研究
邓伟+王少华+张露
摘要:介绍了基于ANSYS软件的CSAMT法三维正演的建模及网格划分方法,研究模型参数设置与卡尼亚视电阻率之间的关系,提出了CSAMT三维正演时模型参数设置建议及规律。研究结果表明:合理设置过渡区可以提高网格划分精度,非均匀划分网格可以有效减少网格数量,提高计算速度;线圈高度的变化会影响磁场垂直入射效果;线圈高度一定时,模型空气层厚度会对视电阻率值产生影响;模型地层厚度会对视电阻率值产生很大影响,测量有效深度与模型地层厚度间存在一定比例关系,从而保证视电阻率值的准确性和规律性。
关键词:CSAMT法;三维正演;ANSYS仿真;临界比例;视电阻率
中图分类号:TP391 文献标识码:A 文章编号:1009-3044(2016)12-0228-04
Abstract: This paper makes an introduction about modeling and meshing of 3D CSAMT forward modeling by ANSYS, researching the relation between model parameters and Cagniard resistivity, coming up with a reference about setting of 3D CSAMT modeling parameters. The results indicate: meshing accuracy is improved by use of transition regionm, inhomogeneous meshing can effictively decrease quantity and enhance simulation rate. Coil height can influence the incoming of magnetic field which should be vertical. When coil height is certain, air thickness of the model influence apparent resistivity. Depth of the ground has a strong influence on apparent resistivity, and there is a proportion relation between surveying depth and ground depth. An appropriate ground depth can keep the simulated result accurate and regular.
Key words:CSAMT; 3D forward modeling; Ansys simulation; critical proportion; apparent resistivity
1 概述
CSAMT法是一种易于操作且成本较低的地质探测手段,它采用有限长线电流源作为激发源,在一定距离外布设测线接收电场和磁场,从而获得卡尼亚视电阻率,并据此判断地表下各地层的地质构造[1]。目前,一维、二维以及2.5维CSAMT法正、反演研究已经较为全面[2-5],理论、模拟都很成熟。但是从实际问题考虑,特别是对于复杂局部地质体的勘探来说,三维CSAMT方法的正、反演才能更客观、准确地反映地质特征[6-9]。
通过理论方法求解三维正反演问题是相当困难,而有限元仿真在解决场问题上有着极大优势,采用有限元仿真软件ANSYS对三维地质模型进行正演模拟[10-11],研究模型建立、网格划分、参数设置、仿真计算、数据提取的方法,为三维CSAMT法正演提供一种参考。
2 ANSYS仿真模拟原理
2.1 CSAMT法视电阻率计算
3 仿真模型建立及视电阻率计算
考虑到工程实际情况,假设模型需要实现探测100m以内的地层视电阻率,即模拟时的有效穿透深度[≥100m]。根据收发距要求,[r=(3~5)h有效≥300~500m],选择收发距[r=500m],模型长、宽为[1km×1.3km];线圈内、外径[8m×12m];初始空气层厚度设为300m,地层设为200m,空气层几乎不导电,电阻率设为[106Ω·m],地层电阻率[ρ0=100Ω·m],线圈施加环向电流,电流密度[Js=10Am2]。
3.1 线圈高度变化与磁场入射角
在线圈内、外径一定时,线圈高度的变化会影响磁场线入射地面时的角度,而卡尼亚视电阻率的计算要求是相互垂直的磁场和电场分量,所以在测量区应该让磁场线尽量垂直入射,以保证计算的准确性。研究线圈磁场时采用二维模型,改变线圈高度,查看测量区[r≥500m]附近的磁场线入射角度。模拟结果如图2所示。
通过改变线圈高度可以看到,随着线圈高度减小,磁场线垂直入射效果越好,当线圈内、外径一定时,高度决定线圈截面积,但场强变化并不会改变磁场方向。进一步研究发现,当线圈高度为200m、100m、60m、30m时,入射角度近似为62°、85°、90°、90°,线圈高度下降到一定值以后就能具有很好的垂直入射效果。后续仿真模拟选取线圈高度为30m。
3.2 网格
三维模型示意如图1所示,整个模型外形为立方体,但线圈处于立方体内部,划分网格时必须进行有效切分且进行有效的网格过渡处理,以保证线圈处以及测量区域网格细化。线圈与边界、测量区与边界之间需有一定距离的过渡区,因为模型并不是无限大,所以模型边界处数据必定存在误差。三维模型网格划分结果如图3所示,在线圈网格外部设置了过渡网格,测量区与边界之间网格由细到粗,自然过渡,空气层网格等比例划分。
对于地层网格,有效深度以内部分采用等距离细网格划分,有效深度以外等比例网格划分。这样处理的好处是既保证了网格划分精度,又可以有效地控制网格数量,提高运算速度。
3.3 不同频率下视电阻率值
根据有效深度计算公式(3),不同激发频率的线圈产生的磁场能够穿透的地层深度不同。模型地层厚度为200m,由公式可推算出穿透10m~200m范围大致的线圈激发频率,首先在200~100000Hz激发频率范围内运行仿真模型,提取测量带中心处的电场、磁场分量,其值如表1所示。再利用公式计算出视电阻率,不同频率下视电阻率计算值如图4所示。
从图中可以看出,在高频区,视电阻率值与设定的电阻率值保持了较好地吻合,但是当场源频率下降到某一值(1000Hz附近)之后,视电阻率值快速增大,偏离真实值。这个结果是与采用有限长导线作为激发源的模拟效果相符的[12]。
3.4 空气层厚度对视电阻率值影响
空气层虽然认为近似不导电,但作为磁场传播介质,其厚度对穿过空气层进入地层的磁场有影响。控制其他参数,仅改变空气层厚度,计算有效深度为20m、30m、40m时的视电阻率值。不同空气层厚度是测量区中心点数据对应视电阻率值如图5所示。
从图中可以看出,在200m空气层厚度时整体偏离地层电阻率值较大,300m~600m范围内视电阻率值趋于稳定。这说明空气层厚度确实会对模拟结果产生影响,可以推测在其他参数一定时,只有当模型空气层厚度超过某一临界值之后,仿真结果才趋于稳定。具体是与线圈高度还是地层深度有关有待进一步探究。
3.5 地层深度对视电阻率值影响
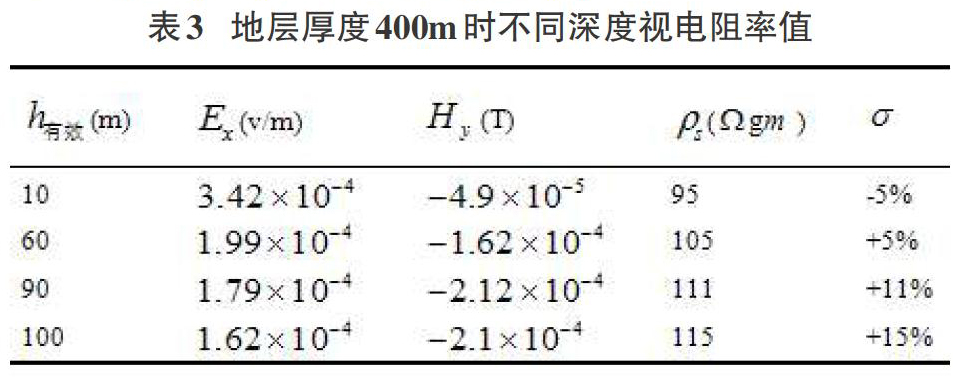
保持模型既定参数不变,空气层厚度设为300m,模型有效穿透深度为100m,根据有效深度计算公式,在10m~100m范围内按照每10m一个测深间隔的顺序,计算出对应谐波电流频率。在ANSYS中通过建立模型多载荷步分析,可一次完成10个频段计算,地层深度200m时视电阻率计算值如表2所示,表中[σ]表示视电阻率值与真实电阻率的偏差。
由表中数据可以看出,此时视电阻率的模拟效果并不理想,视电阻率值与真实值偏差范围达到了-26%~66%,测深100m时的视电阻率值更是远远偏离实际值。通过查看浅层地层和深层地层的感应电场线可以发现,浅层时的感应电场线是较为规则的,而一定深度后电场线将逐渐发生变形,越靠近边界这种现象越明显,这必将影响视电阻率计算值的准确性。
当探测深度为一定值时,应该对模型的地层深度适当加深,以保证提取数据的深度范围电场线变形较小。因此,改变模型地层深度,查看在不同深度下10m~100m范围内视电阻率值如何变化。
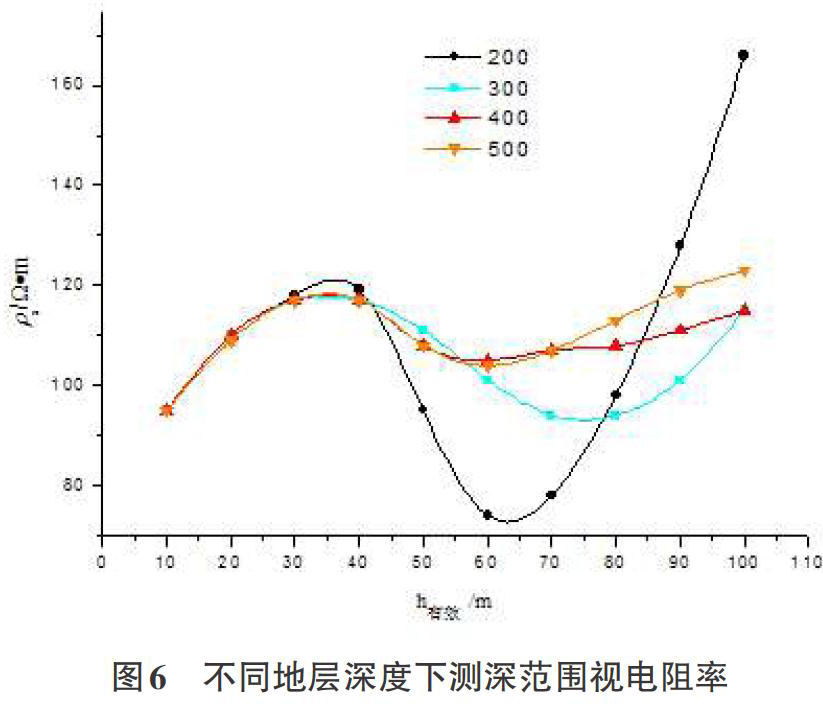
在300m~500m范围内改变地层深度,计算200m、300m、400m、500m深度下各频段的视电阻值,结果如图6所示。
可以看到,随着深度的增加,视电阻率值计算值逐渐趋于稳定,偏离程度减小。在400m时,10m~100m有效深度范围内,如表3所示,视电阻率值偏离真实电阻率值范围在-5%~15%,这已经能够很好的反映地层电阻率特征。
同时,由图6还可以发现,测深范围在10m~40m范围内时,地层深度200m~500m范围视电阻率值几乎相同,即测深[≤40m]时,地层深度设为200m即可确保计算准确性;而当有效深度为50m~60m时,只有在300m~500m范围视电阻率值接近,即地层深度[Hd≤60m]时,地层深度设为300m可保证计算准确性;最后,当有效深度范围为70m~100m时,地层深度取为400m~500m均可得到较为理想的视电阻率值。由上述分析可以发现,为了确保模型计算出的视电阻率值准确性,有效测量深度和地层深度之间存在着一个比例关系,在本文研究的参数下,比例系数大致为1:5,即地层深度为有效深度5倍时,可保证较好仿真效果。
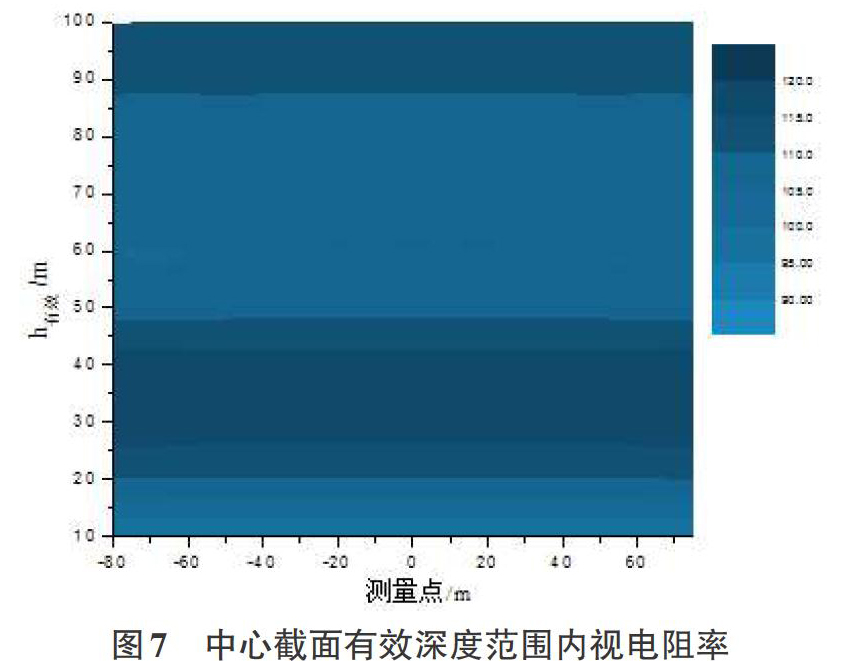
地层深度为400m时,误差上下限已经比较理想,此时,再提取测量带中心截面上以测量带中心为原点,-80m~80m范围内9个点的磁场、电场值,计算截面视电阻率。结果如图7所示。
通过截面视电阻率图可以看出,在-80m~80m范围内,视电阻值保持了很好的准确性。说明采用上述的模型处理方法进行三维正演的仿真,可以得到较好模拟效果。
4 结论
通过建立三维有限元仿真模型并对模型进行有效地网格处理、参数设置,得出了进行CSAMT三维正演模拟一些有参考价值的结论,具体如下:
①采用线圈作为激发源进行模拟仿真,有别于传统的偶极源激发源,卡尼亚视电阻率值能够很好反映测量区电阻率。线圈高度会影响磁场入射地面的角度,划分模型网格时,在线圈、测量区处要进行网格细化,模型各部分之间采用过渡网格、等比例划分网格可以保证运算精度并提高运算速度。
②空气层厚度对仿真结果有影响,当模型要求测深一定时,空气层厚度需要超过一临界值才能保证视电阻率计算值的准确性。
③地层厚度直接影响视电阻率计算值,只有合理调整纵向地层厚度才能保证一定范围内视电阻率值的准确性,总的规律是随着电磁波测量有效深度的增加,地层厚度需要增加。且在探测范围[≤]100m时,有效深度与地层厚度之间存在近似1:5的临界比例关系,模型地层厚度设为有效探测深度的5倍可以保证很好的仿真效果。
文中仅探究了以线圈为激发源的三维CSAMT法正演的有限元仿真实现方法以及部分参数的变化规律,主要是模型高度方向变化规律,对CSAMT三维正演研究提供一种参考,为下一步引入吸收边界的视电阻率研究提供基础支撑。模型长度与宽度对仿真应该也有一定影响,有待进一步研究并总结出更全面的规律。
参考文献:
[1] 底青云,王若.可控源音频大地电磁数据正反演及方法应用[M].北京:科学出版社,2008.
[2] 王若,王妙月.一维全资料CSAMT反演[J].石油地球物理勘探,2007,42(1):107-110.
[3] 龚强.CSAMT二维正演研究[D].北京:中国地质大学,2007.
[4] 郑仁淑,钟宏伟.地表上方电偶极源响应特征研究[J].工程地球物理学报,2005,2(5):349-350.
[5] 许广春.CSAMT法在实际应用中的若干问题[J].物探与化探,2011,35(6):810-812.
[6] 王若.CSAMT三维单分量有限元正演[J].地球物理学进展,2014,29(2):840-843.
[7] 陈锐.CSAMT三维交错采样有限元差分数值模拟并行算法研究[D].北京:中国地质大学,2012.
[8] 黄临平,戴世坤. 复杂条件下三维电磁场有限元计算法[J].地球科学—中国地质大学学报,2002,27(6):775-780.
[9] 阎述,陈明生. 电偶极源频率电磁测深三维地电模型有限元正演[J]. 煤田地质与勘探,2000(3):50-56.
[10] 张倩.ANSYS 12.0电磁学有限元分析从入门到精通[M].北京:机械工业出版社,2010.
[11] 谢龙辉,耿煜,邱婉. ANSYS电磁场分析[M]. 北京:电子工业出版社,2012.
[12] 王若,王妙云,卢元林. 三维三分量CSAMT法有限元正演模拟研究初探[J]. 地球物理学进展,2007,22(2):584.

