1100铝合金Taylor杆撞击变形与断裂数值模拟研究

2023.03.15

魏刚冯岩

摘要：Taylor杆撞击实验指的是平头金属杆弹正撞击光滑的刚性板，其最初目的用来获取材料动态性能参数或者进行材料动态本构方程的验证。将Taylor杆撞击速度进一步提高，可以使圆柱弹体发生开裂、开花甚至破碎失效，为研究冲击载荷下材料的断裂失效行为的提供了一个较好的手段。本文在已有1100铝合金Taylor杆撞击实验结果的基础上，结合材料性能测试，开展了对应的ABAQUS/EXPLICT数值模拟研究，获得了与撞击实验一致的变形和断裂模式，且各变形与断裂模式的速度范围和实验也非常吻合。在此基础上，提取数值模拟中失效单元的关键信息，揭示了1100铝合金Taylor杆撞击失效机理。

关键词：1100铝合金;Taylor杆撞击;数值模拟;变形与断裂模式;失效机理

1 概述

1100铝合金指含铝量99.0%的普通工业纯铝，不可热处理强化，强度较低，但延展性非常好。前期为了研究高延性材料在冲击载荷下的变形与断裂特性，在轻气泡上开展了1100铝合金Taylor杆撞击实验[1，2]，弹体名义尺寸Φ12.6mm×50.4mm，名义质量17 g。典型的实验结果列于表1中，其中mi，Li和Di分别为弹体的初始质量，初始长度和直径;V0为弹体初始撞击速度;Lf和Df为弹体剩余长度和头部直径，Lunc为弹体未变形长度，Npetals为发生花瓣断裂的弹体花瓣数目，弹体初始及Taylor撞击变形后的尺寸测量方式如图1所示[1，2]。回收到弹体的典型变形与断裂模式参见图2[1，2]。在前期实验基础上，结合材料性能测试，利用ABAQUS/EXPLICT开展与试验工况对应的数值模拟研究，在验证有效性的基础上，利用数值模拟对1100铝合金Taylor杆的断裂机理进行分析。

为了集中关注弹体变形和断裂，靶板均采用弹性钢靶，即弹性模量取为200GPa，且不考虑弹靶之间的接触摩擦。

3 数值模拟结果及分析

3.1 数值模拟结果及有效性验证

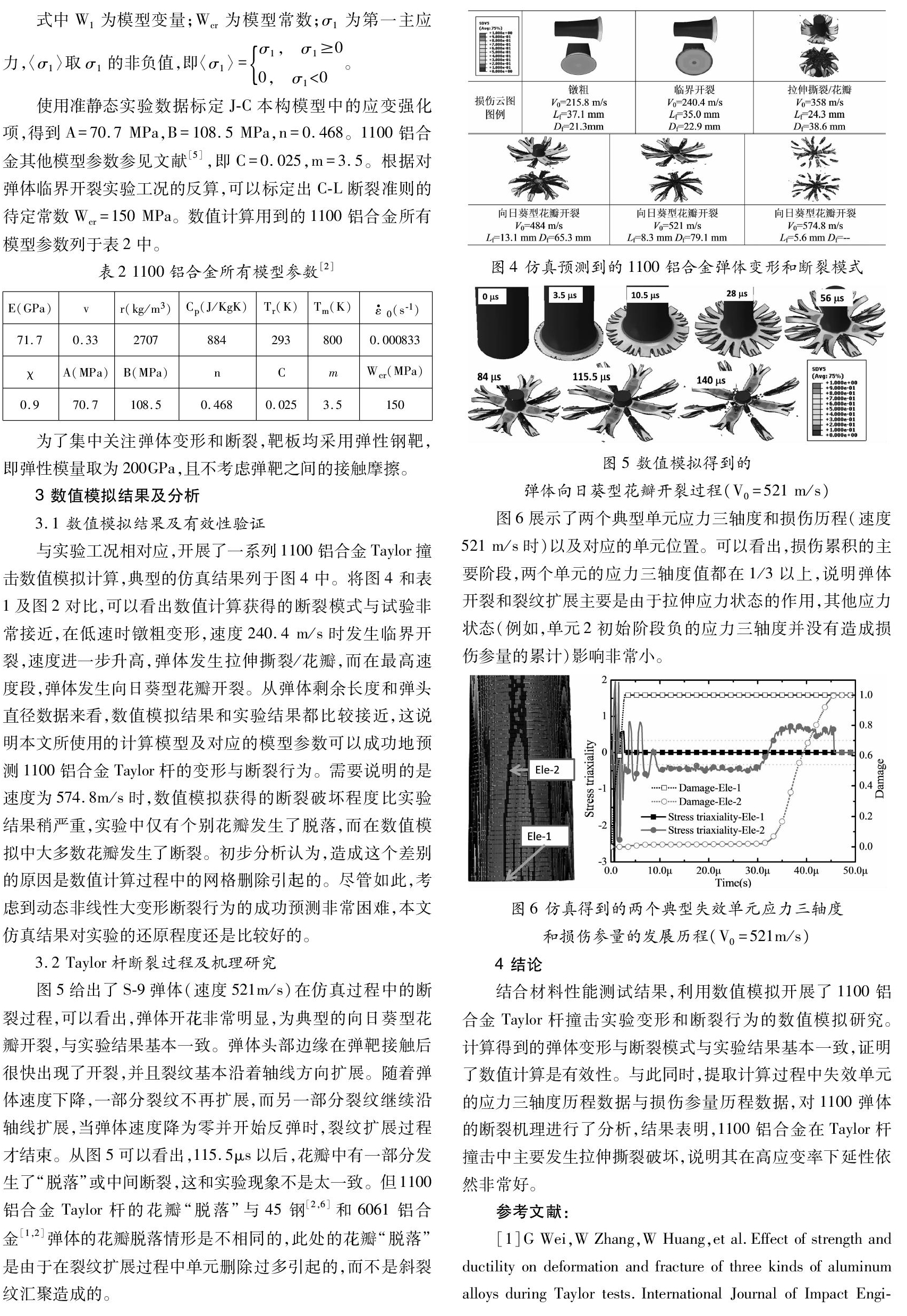
与实验工况相对应，开展了一系列1100铝合金Taylor撞击数值模拟计算，典型的仿真结果列于图4中。将图4和表1及图2对比，可以看出数值计算获得的断裂模式与试验非常接近，在低速时镦粗变形，速度240.4 m/s时发生临界开裂，速度进一步升高，弹体发生拉伸撕裂/花瓣，而在最高速度段，弹体发生向日葵型花瓣开裂。从弹体剩余长度和弹头直径数据来看，数值模拟结果和实验结果都比较接近，这说明本文所使用的计算模型及对应的模型参数可以成功地预测1100铝合金Taylor杆的变形与断裂行为。需要说明的是速度为574.8m/s时，数值模拟获得的断裂破坏程度比实验结果稍严重，实验中仅有个别花瓣发生了脱落，而在数值模拟中大多数花瓣发生了断裂。初步分析认为，造成这个差别的原因是数值计算过程中的网格删除引起的。尽管如此，考虑到动态非线性大变形断裂行为的成功预测非常困难，本文仿真结果对实验的还原程度还是比较好的。

3.2 Taylor杆断裂过程及机理研究

图5给出了S-9弹体（速度521m/s）在仿真过程中的断裂过程，可以看出，弹体开花非常明显，为典型的向日葵型花瓣开裂，与实验结果基本一致。弹体头部边缘在弹靶接触后很快出现了开裂，并且裂纹基本沿着轴线方向扩展。随着弹体速度下降，一部分裂纹不再扩展，而另一部分裂纹继续沿轴线扩展，当弹体速度降为零并开始反弹时，裂纹扩展过程才结束。从图5可以看出，115.5μs以后，花瓣中有一部分发生了“脱落”或中间断裂，这和实验现象不是太一致。但1100铝合金Taylor杆的花瓣“脱落”与45钢[2，6]和6061铝合金[1，2]弹体的花瓣脱落情形是不相同的，此处的花瓣“脱落”是由于在裂纹扩展过程中单元删除过多引起的，而不是斜裂纹汇聚造成的。

图6展示了两个典型单元应力三轴度和损伤历程（速度521 m/s时）以及对应的单元位置。可以看出，损伤累积的主要阶段，两个单元的应力三轴度值都在1/3以上，说明弹体开裂和裂纹扩展主要是由于拉伸应力状态的作用，其他应力状态（例如，单元2初始阶段负的应力三轴度并没有造成损伤参量的累计）影响非常小。

4 结论

结合材料性能测试结果，利用数值模拟开展了1100铝合金Taylor杆撞击实验变形和断裂行为的数值模拟研究。计算得到的弹体变形与断裂模式与实验结果基本一致，证明了数值计算是有效性。与此同时，提取计算过程中失效单元的应力三轴度历程数据与损伤参量历程数据，对1100弹体的断裂机理进行了分析，结果表明，1100铝合金在Taylor杆撞击中主要发生拉伸撕裂破坏，说明其在高应变率下延性依然非常好。

参考文献：

[1]G Wei，W Zhang，W Huang，et al.Effect of strength and ductility on deformation and fracture of three kinds of aluminum alloys during Taylor tests.International Journal of Impact Engineering，2014，73：75-90.

[2]魏刚.金属动能弹变形与断裂特性及其机理研究[D].哈尔滨工业大学，2014.

[3]GR Johnson，WH Cook.A Constitutive Model and Data for Metals Subjected to Large Strains，High Strain Rates and High Temperatures.Proceedings of the seventh international symposium on ballistics，Hague，Netherlands.1983：541-547.

[4]MG Cockroft，DJ Latham.Ductility and the Workability of Metals.Journal of the Institute of Metals.1968，96：33-39.

[5]DJ Steinberg.Equation of State and Strength Properties of Selected Materials.Lawrence Livermore National Laboratory.1991.

[6]魏剛，张伟，邓云飞.基于J-C模型的45钢本构参数识别及验证.振动与冲击，2019，38（05）：181-186.

项目：本文受中国民航大学科研启动基金基金项目（2015QD01S）资助

作者简介：魏刚（1987—），男，博士，讲师，研究方向：冲击动力学与材料力学性能测试。