小波变换在信号奇异性特征检测中的应用

    龙腾飞　郭巍　申睿

    

    

    

    摘 要：奇异性检测在类似故障诊断这样的工程应用中意义非凡，其中一项就是关于信号故障奇异性特征的提取。通过数学软件Matlab做了关于小波变换在噪声信号的奇异性特征和故障信号检测中的仿真实验。结果表明，小波分析在非平稳信号特征检测中有着较好的稳定性和可靠性。

    关键词：小波变换；奇异点；模极大值；Matlab仿真

    近年来，小波分析理论成为众多学术团体和学科领域共同关注的热点。它是应用数学家和数据处理工程师在各自领域研究中分别独立发现的。随着小波分析在应用数学和工程科学领域的迅速发展，尤其是计算机和信息处理技术的普及，其在信号特征检测中的应用越来越受到人们的关注。对于稳定不变的信号来说，傅立叶分析是理想的处理工具，但在实际工程应用中由于绝大多数信号是非平稳的，其最佳处理工具则是小波分析。

    1 信号奇异性的相关理论[1-2]

    奇异信号也称突变信号，在诸如图像边缘检测、机械故障诊断、电力系统故障、脑电图、心电图的异常等实际问题中，每一个细小的变化都对应着信号的突然变化。因此，研究信号的奇异性突变检测有着十分重要的意义。

    1.1 奇异信号的种类

    一般说来，信号的奇异性有两种：一种是其幅值在某一时刻内由于发生了突变而产生了非连续信号，我们把其幅值的突变点称为第一类间断点；另一种是信号的外观很光滑且幅值不发生突变，而信号的一阶倒数有突变但不连续，我们把幅值的突变点称为第二类间断点。

    1.2 信号奇异性与Lipschitz指数

    信号的奇异点表征了信号的突变特征，有时表现为间断或尖峰，有时则表现为某阶导数的不连续。从数学的角度分析，如果函数f（t）存在间断点或其某阶导数不连续，则称该间断点为函数f（t）的奇异点。转换成信号领域，我们习惯用利普西兹指数（Lipschitz）α来刻画信号f（t）在该点处的奇异程度。

    一般情况下，我们用某一点处的利普西兹指数α表征信号函数f（t）在该点处的奇异性大小：α越大信号的光滑度越好，在该点处拥有越小的奇异性；反之，α越小信号的光滑度越差，在该点处拥有越大的奇异性。

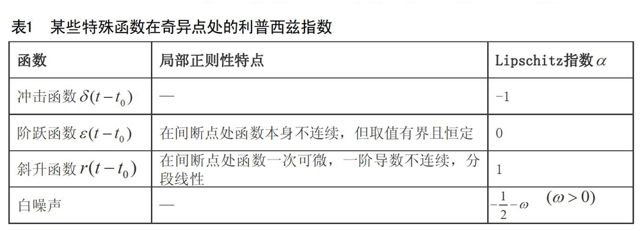
    如果信号函数f（t）在时间点t0处可导，则该点的利普西兹指数α>1；如果f（t）在t0连续不可导，则该点的利普西兹指数α=1；假若f（t）在t0点不连续且其值有限，则该点的利普西兹指数0<α<1。如表1所示，给出了冲击函数、阶跃函数、斜升函数以及白噪声在奇异点处的利普西兹指数一览。

    2 小波变换在奇异性信号检测中的应用

    2.1 小波变换与信号的奇异性检测的相关理论

    在工程应用中，故障的发生往往会带来信号峰值的突然变化。因此，研究奇异点所隐含的信息将为解决实际问题提供极大帮助[3]。

    研究表明，小波变换的模极大值与变换尺度和奇异指数α之间有如下关联：当α=0时，无论尺度如何变化，小波变换的模极大值都不变；当α>0时，随着尺度的增大，小波变换的模极大值跟着增大；当α<0时，随着尺度的增大，小波变换的极大值随之减小。白噪声是一种特殊的随机分布信号，它的利普西兹指数保持α<0，故随着尺度的增大，其小波变换的极大值将减小。

    据此，结合已有研究成果可以进一步推导得出：信号f（t）的小波变换模极值点就是它自身的信号奇异点，描述该奇异点特征的利普西兹指数则可以通过计算小波变换尺度的衰减细况得到。

    2.2 仿真实验

    2.2.1 故障奇异信号检测的Matlab仿真

    系统如果发生故障会出现噪声信号，我们可以通过小波变换提取噪声特征的方式进行系统故障的精确定位，进而做到故障修复。

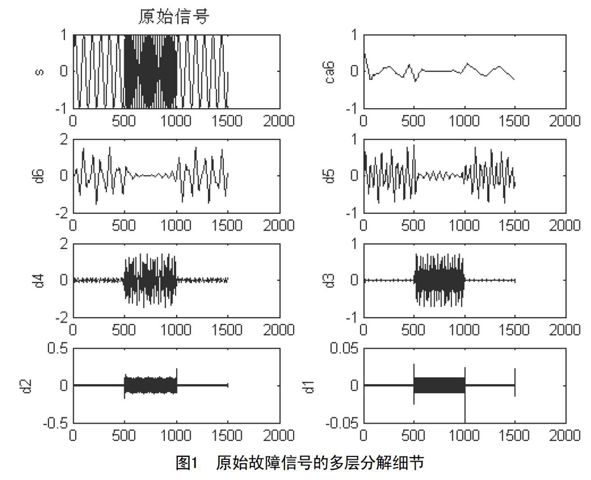
    在仿真实验中，对信号f（t）先进行多尺度分解，随后重构其不同尺度的高频部分[4，5]，得到了相应的噪声成分。实验中使用db3小波基对系统异常时的输出信号进行了六层多分辨率分析。如图1所示。

    仿真结果分析：由图1可以看出，该实例中出现的间断点是第一类间断点，通过db3小波对信号进行多尺度分析，由细节信号可以很明显判断出故障的位置，在t=500时，系统出现了异常情况，在t=1000时，系统工作恢复了正常。观察图1，可以发现经过用db3小波对系统异常时输出信号进行六层多分辨率分析的过程，实际上是每层分解是用不同的高、低通滤波器对上一层的低通信号进行滤波处理，最终的分解信号中第六层的低频信号ca6是得到的信号的低频成分，而经过六层分解得到的高频信息成分分别为dl、d2、d3、d4、d5、d6，它们在频率分辨率和时间分辨率两项数据上的表现刚好相反，即频率分辨率越来越高，而时间分辨率会越来越小。第一层分解的d1高频系数清楚地确定了故障信号所持续的时间段。

    2.2.2 用Matlab检测噪声奇异信号

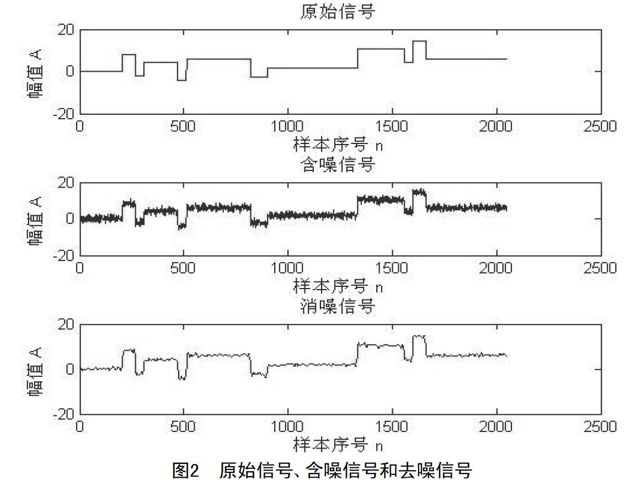
    在实际应用中，信号往往都夹杂着噪声，这无疑增加了检测奇异点的难度。本仿真实例中引入的是一个含高斯白噪声的矩形波信号，如图2所示。在利用小波变换对含噪信号进行奇异点检测时有两种方法：一是对含噪信号采用适当的处理方法进行去噪处理，然后对消噪信号进行小波分解；二是利用小波函数对含噪信号f（t）进行直接分解，通过分解出来的的第一层细节信号特征估算出噪声所在的大体位置，进而在小波分解的更深层次上展现出信号的奇异点[5，6]。

    使用db3小波对原始信号进行六层多分辨率分析，得到的小波分解图，如图3所示，在第一层细节信号中可以清晰地看到奇异点的位置。接下来，对含噪信号进行去噪处理，即抑制信号中的无用部分，增强信号中的有用部分。观察图2，处理后的信号大体上保留了初始信号的特征，同时去除了噪声干扰，去噪效果比较明显。对消噪信号进行小波分解，由第一层和第二层细节信号能够粗略地判断出奇异点的位置，而直接对含噪信号进行小波分解，第一层细节信号噪声影响是很明显的，信号奇异性在更深层次的细节信号d3、d4表现了出来，如图4所示。

    因此，如果一个系统发生了故障，往往会带来输出信号的奇变，所混杂的噪声信号也会随之增强。因此，在提取系统输出信号特征时进行去噪处理，同时重点分析系统输出信号的高频分量特征可以有效实现系统故障的检测。

    3 结语

    小波变换在信号处理中被称为显微镜，通过局部模极大值的性质能精确分析信号在小波变化下的局部奇异性，给出各奇异点的位置。实验表明，小波变换在故障信号、噪声信号的奇异性特征检测方面有着较好可靠性和稳定性，正成为当前应用数学和工程学科中一个迅速发展的新领域。

    [参考文献]

    [1]李章勇，姜瑜，王伟，等.基于小波变换的皮电信号滤波及奇异性检测[J].科学技术与工程，2013（4）.

    [2]陈光，俞金方，杨清华.一种基于小波奇异值检测的鱼雷电磁引信目标信号特征识别方法[J].鱼雷技术，2013（1）.

    [3]陈克祥.多小波理论在输电线故障定位中的应用研究[D].合肥：安徽大学，2012.

    [4]洪从鲁，赵慧.小波变换在输电线路故障检测中的应用[J].信息通信，2012（4）.

    [5]廖晓辉，梁恒娜，丁倩. 基于小波变换的电力电缆故障测距研究[J].郑州大学学报：工学版，2013（3）.

    [6]魏阿妮.基于小波变换的心电信号奇异性的检测分析研究[D].西安：陕西师范大学，2012.