失谐连续双跨梁结构振动特性的理论和实验研究

2023.03.15

周盛林　李凤明

摘要：基于Euler-Bernoulli梁理论建立了双跨梁结构的动力学模型，采用模态分析方法求解动力学方程，根据边界条件获得双跨梁的频率方程，由此求解出双跨梁的固有频率，以此为基础进一步得到结构各点的时间响应历程曲线。针对双跨梁的两跨长度不等长造成的结构尺寸失谐，分析了不同跨长比对结构振动特性的影响，将理论计算结果与有限元仿真和实验结果进行比较，得到了较好的吻合。研究结果对于工程领域中失谐双跨梁结构的动力学分析和设计具有一定的参考价值。

关键词：双跨梁；失谐；振动特性；实验研究

中图分类号：0326；TBl23

文献标志码：A

文章编号：1004-4523（2017）01-0149-06

DOI：10.16385/j.cnki.issn.1004-4523.2017.01.020

引言

周期多跨梁结构在航空航天、高速列车、土木建筑、机械工程等多个领域都具有广泛应用，由于多跨梁结构的复杂性，对其动力学行为的研究是动力学与控制领域的难点问题，逐渐受到国内外力学界专家学者的重视。目前为止，针对梁结构的研究大多集中在单跨梁上，对于多跨梁的研究主要集中在周期谐调梁上。周期多跨梁在实际加工制作过程中，由于制造误差或者实际工程需要，会出现各个子结构尺寸不相等、材料参数差异等各种失谐情况。而失谐多跨梁由于结构的特殊性，对其动力学问题的分析比较复杂，迄今为止，对于失谐多跨梁动力学特性的研究还比较少，因此有必要针对失谐多跨梁结构的动力学特性展开深入研究。

对于谐调和失谐多跨梁振动特性的研究，采用较多的方法是模态展开法、传递矩阵法等。Mikata采用模态展开法研究了多跨梁结构的模态正交性，给出了谐调双跨梁结构动力学响应的计算方法。Li和Song采用模态展开法研究了失谐双跨梁的振动特性及其控制问题，分析了失谐程度对结构振动行为和控制效果的影响。Li和Wang采用传递矩阵方法研究了随机失谐多跨梁的振动局域化问题，研究发现结构的尺度失谐会导致周期结构的频率通带区间变小甚至消失，出现振动局域化现象。基于波传递矩阵方法，Bouzit和Pierre[93研究了双耦合多跨梁中的波动局域化和能量转化现象，研究发现跨长的小量失谐也会导致振动能量局限在结构的局部区域，并且能量可以在不同的波模态之间转化。Chen和Wang采用传递矩阵法研究了周期Timoshenko梁结构中弯曲波的主动控制问题。

虽然目前对于失谐多跨梁的动力学问题已经有了一些研究结果，但是有关该问题的研究多集中在理论研究上，实验研究结果还不多见。本文针对失谐双跨梁结构进行分析研究，基于Euler-Bernoulli梁理论建立双跨梁的动力学模型，根据边界条件获得双跨梁的频率方程，求解此超越方程获得结构的各阶固有频率，进而得到结构的响应时间历程曲线。采用振动实验测试技术和有限元仿真方法，对失谐双跨梁结构的动力学特性进行研究，将所得有限元仿真和实验结果与相应的理论计算结果进行比较，验证了理论计算结果的正确性。此外，分析了梁的截面高度及失谐双跨梁的不同跨长比对结构振动特性的影响规律。

1.结构运动方程的建立和求解

如图1所示，双跨梁左右两端均为铰支，中间支承也是铰支。梁截面为矩形，梁截面的高度与宽度分别为h和6，I为梁的截面惯性矩，L1和L2分别为双跨梁的各跨长度，梁的横截面积为A，材料的弹性模量为E，密度为p。

从表1可以看出，本文的理论解与有限元仿真结果吻合较好，尤其在低频区域吻合很好，前5阶固有频率的相对误差在3%以内，从而验证了本文理论分析方法的可行性。

2.2参数变化对双跨梁固有频率的影响

在上述算例的基础上，进一步研究几何参数h和各跨不同跨长比（短跨与长跨的比值）对结构固有频率的影响。表2给出了针对跨长比为0.67時，失谐双跨梁的固有频率随梁高度h的变化情况；表3给出了双跨梁的固有频率随跨长比的变化情况。失谐双跨梁的固有频率随梁截面高度增加而增加，并且增加速度较快，这说明梁的截面高度对其固有频率影响较大。从表3可以看出，双跨梁的高度取0.0009m、其他参数不变时，跨比越大，梁的第一阶固有频率越高（跨比为1时对应谐调双跨梁）。同时可以发现，跨比对双跨梁的低阶固有频率影响较大，越到高阶随着跨比的变化频率的偏差率越小。

3.失谐双跨梁的自由振动分析

3.1理论研究

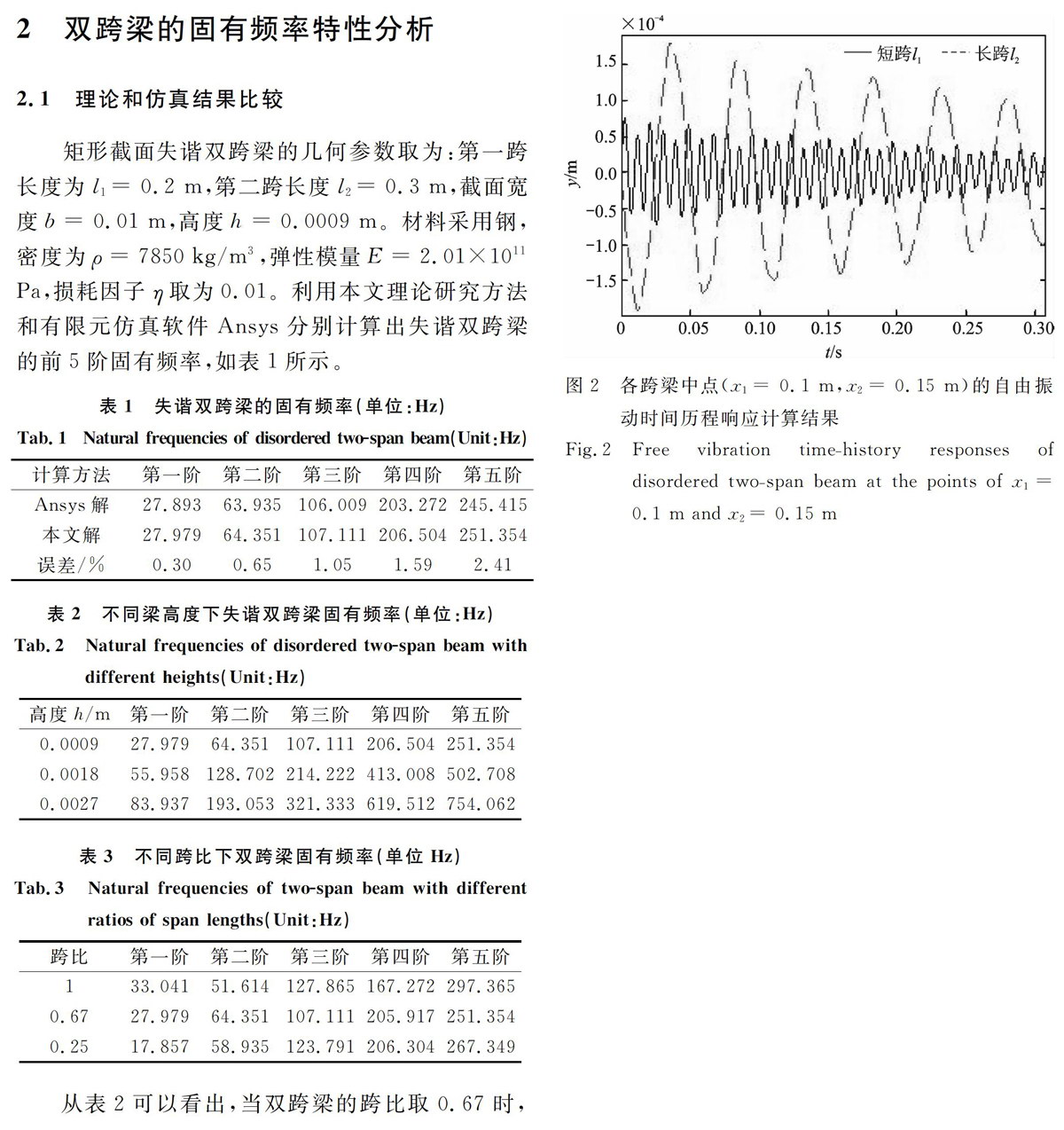
在上述结构固有频率研究的基础上，本小节将采用理论方法对失谐双跨梁的自由振动特性进行分析研究。失谐双跨梁的结构和材料参数取值与第2.1节中的取值完全相同。分别计算各跨梁的中点、以及关于中间支撑的对称点的自由振动时间历程响应，并进行对比分析。具体计算结果如图2和图3所示。

从图2和3可见，对于各跨梁上的对应点，长跨梁的振幅比短跨梁的振幅大，另外可见，考虑结构阻尼的影响时，随着时问的增加，双跨梁的振动响应幅值逐渐降低。同时，短跨梁的振动频率与长跨梁的振动频率不一致，短跨梁的振动频率要高一些。根据图2和3中的响应曲线可计算出，长跨梁的振动频率为27.9Hz，短跨梁的振动频率为64.5Hz。对比表1中双跨梁结构的各阶固有频率可知，长跨梁主要以整体双跨梁的第一阶固有频率做自由振动，同时受到二阶固有频率的影响；短跨梁以第二阶固有频率做自由振动，同时也受到一阶固有频率的影响。失谐双跨梁的这些特殊振动特性在实际工程应用中应该加以注意。

3.2实验研究

通过上一小节的理论分析可知，失谐双跨梁的每一跨分别以不同的频率和振幅做自由振动。为了进一步验证上面理论分析结果的正确性，本小节将开展失谐双跨梁的自由振动实验研究。

实验模型严格按照第3.1节理论研究中的结构和材料参数设计，具体实物模型和实验装置如图4和5所示。其中在双跨梁模型的支承位置处焊接一个带有光滑孔洞的圆环，而支承钢片上的螺杆则穿过圆环，实现了梁可转动的简支边界条件；中间支承和右边支承将圆环孔洞水平方向留稍大一点空间，即实现了滑动简支的效果。在实验过程中，采用LMs公司的力锤进行敲击，使用具有高稳定性的基恩士（LK-Navigator）激光位移传感器测试，并记录测试点的实时位移响应，利用Matlab对所测点实验数据分析绘图，并比较分析所得实验数据。

实验时需控制好力锤，以较小的力敲击梁，使梁的变形处于线弹性范围内，以便实验结果与理论结果相符，同时需要注意力锤敲击的方式，防止二次碰撞。安置好光测传感器，对准测试点，打开信号处理器和计算机，设置好测试通道和测试点数以及数据存储方式。调整好锤击角度，开始敲击。

与3.1节中理论分析相对应，分别取各跨梁中点、以及关于中间支撑的对称点的时程历程响应进行测试分析，具体实验结果如图6和7所示。由图6和7可见，对于两跨梁上的对应点，显然长跨的振幅比短跨的振幅大，并且短跨的振动频率与长跨的振动频率不一致。各跨梁以某階频率做振动，同时受到另外一阶频率的影响。通过分析图6和7可知，长跨梁和短跨梁的振动频率分别为26.3Hz和62.1Hz，与第3.1节中的理论计算结果（27.9Hz和64.5Hz）吻合较好，从而验证了理论分析结果的正确性。

此外，由图6和7还可以看出，实验测得的结构时间历程响应曲线随着时问的增加，响应幅值逐渐衰减，主要原因是实验试件双跨梁简支处的摩擦产生了阻尼，以及实验过程中存在结构阻尼和空气阻尼等。同时可以发现，结构响应幅值降低的程度与考虑了结构阻尼效应的理论计算结果（图2和图3）吻合较好。

5.结论

针对失谐连续双跨梁结构的自由振动问题进行了理论和实验研究，理论分析结果与有限元仿真和实验结果吻合较好。通过研究表明，本文理论分析方法具有较高的精确度，计算量也比较小，能够更加简单直接地在本论文基础上进行结构的优化设计。通过分析研究，可以得到如下结论：

（1）失谐双跨梁的固有频率随梁截面高度的增加而增加，并且增加速度较快；不同跨长比下，比率越大，梁的一阶固有频率越高。

（2）跨长比对双跨梁的低阶固有频率影响较大，越到高阶，跨长比的变化对结构固有频率的影响越小。

（3）对于各跨梁的对应点，长跨梁的自由振幅幅值比短跨梁的大；短跨梁和长跨梁分别以不同的频率做自由振动，短跨梁的振动频率要高一些。

（4）理论和实验分析表明，长跨梁主要以整体失谐双跨梁的第一阶固有频率做自由振动，同时受到二阶固有频率的影响；短跨梁以整体结构的第二阶固有频率做自由振动，同时受到一阶固有频率的影响。

本文的研究结果和方法对于工程领域中失谐双跨梁结构的动力学分析和设计具有一定的参考价值。