时频脊融合方法及时变工况行星齿轮箱故障识别
江星星 李舜酩 周东旺 陈远帆 石娟娟


摘要:行星齿轮箱的瞬时频率(转速)精确提取是行星齿轮箱时变运行工况下故障诊断的关键。现有一些时频脊提取算法在提取瞬时频率时受到振动信号幅值变化以及时频变换结果中噪声成分的干扰,存在鲁棒性问题。为了解决这一问题,提出了一种双向搜索时频脊融合方法,并且将其进一步推广到多时频脊融合的概念中。然后,应用提出方法提取实际工程中时变工况行星齿轮箱高速轴的瞬时转速。再通过与现有两种方法对比以及阶次分析,验证了时频脊融合方法提取高速轴转速的可靠性与准确性。最后,在行星齿轮箱转速提取的基础上,利用阶次分析以及推导出的行星轮轴承故障频率的计算式,识别出了行星齿轮箱中的行星轮轴承内圈存在故障。
关键词:故障诊断;行星齿轮箱;时频脊;阶次分析;瞬时频率
中图分类号:THl65+.3;TN911.7
文献标志码:A
文章编号:1004-4523(2017)01-0127-08
DOI:10.16385/j.cnki.issn.1004-4523.2017.01.017
引言
2014年12月法国里昂大学举办的CMMNO(Condition Monitoring of Machinery in Non-sta-tionary Operation)会议发出行星齿轮箱“挑战”,要求“针对某实际工程中时变工况状态下的行星齿轮箱,从其振动信号中提取齿轮箱高速轴转速以及识别出齿轮箱出现轴承故障的部位”。笔者作为来自13个国家的23个参加者之一参与“挑战”。
行星齿轮箱在车辆、直升机和风力发电机组的传动系统中应用广泛,其故障诊断问题不容忽视。振动信号分析是齿轮箱状态监测的一种常用且有效的技术手段。行星齿轮箱运行工况的变化导致振动信号呈现非线性、非平稳特性,造成传统的时域和频域分析方法失效。时频分析将一维信号变换到由时问和频率离散点组成的网格面,能有效地揭示非平稳信号中蕴含各分量随时间变化的特征。常见的时频分析方法,像wigner-Ville分布、以Wigner-ville分布为基础的双线性时频分布、Hilbert-Huang变换、小波变换等各有优缺点。在考虑到本文分析信号具有数据量特大、蕴含分量非常多的特点,同时为使目标时频脊线具有足够的分辨率,采用計算效率高且满足工程要求的短时傅里叶变换(short Time Fou-rier Transform,STFT)作为时频分析工具。
从时频矩阵中精确地估计参考轴转速对应的瞬时频率是实现无转速计信号参照的行星齿轮箱故障诊断重要一步。最简单的时频脊提取算法是峰值检测法,但也最易受噪声成分干扰。文献[12-13]针对连续小波变换得到的时间一尺度平面,采用具有时频点幅值和相邻点频率波动的两项约束建立代价函数提取时频脊,然后文献[14]针对时一频面提出了与其相似的脊线搜索法。文献[11]为了避免对初始搜索点位置的限制,也利用相同的代价函数建立了双向时频脊搜索算法。这类代价函数只利用了相邻时频点信息,一旦时频面局部位置出现强噪声或干扰分量的影响,易造成脊线提取失效。小波脊线提取方法也常用于脊线提取,对单分量或多分量信号中高能量的分量提取效果较好,但对于多分量信号中能量较弱的分量难以识别。
因CMMNO会议发出“挑战”的行星齿轮箱的转速变化,造成信号中蕴含多分量的瞬时频率和幅值都随时间发生改变,且待提取的目标脊线能量较弱。为此,仅仅采用单一代价函数或模极大值提取时频脊,会因信号幅值变化和噪声的干扰,造成脊线提取失效。针对此问题,提出一种双向搜索时频脊融合方法。主要思想是利用单一代价函数得到多条脊线,再根据脊线差值中包含的信息,以突变特征来识别融合区间,将各条脊线中最接近真实脊线的信息进行合并,实现行星齿轮箱高速轴的转速的提取,以解决单一时频脊不能兼顾目标分量在时频面内全局变化的问题。最后,利用阶次方法识别故障轴承的位置。
1.行星齿轮箱“挑战"及其初步分析
“挑战”的行星齿轮的结构示意图如图1所示,量多,而小波变换具有频率分辨率随分解尺度变化的特性,造成中高频分量混叠。此外,由图4(时问、频率分辨率分别为1s,0.5Hz)可以知,分析信号中各分量的频率和幅值变化剧烈,其中箭头1,5指示信号中两个能量较大、频率变化的分量位置;箭头4所示为一能量较弱、频率变化的分量;箭头2,3其中各齿轮参数如表1所示。振动信号采集过程中,其输入转速大致在13~15r/rain之间,采样频率为5000Hz,采样时间在548s左右。信号时域波形如图2所示,可以看出其幅值随时间变化较明显。观察图3频谱图中可知信号大部分能量集中在0~2000Hz。为了揭示信号蕴含各分量的本质,图4,5分别为信号的两种时频分布。短时傅里叶变换对于中、高频分量的表示明显优于连续小波变换(复morlet小波基,主要是因为信号中的中、高频分所示为频率不变两分量,“挑战”方告知采集传感器置于齿轮箱附近电机侧,可推测与电机产生的高频干扰分量或与齿轮箱结构固有频率相关。
由行星齿轮箱中各齿轮对运动关系,输入轴转速与高速轴(齿轮7所在轴)传动比iiH为
3.高速轴转速提取及其准确性验证
3.1行星齿轮箱高速轴转速提取
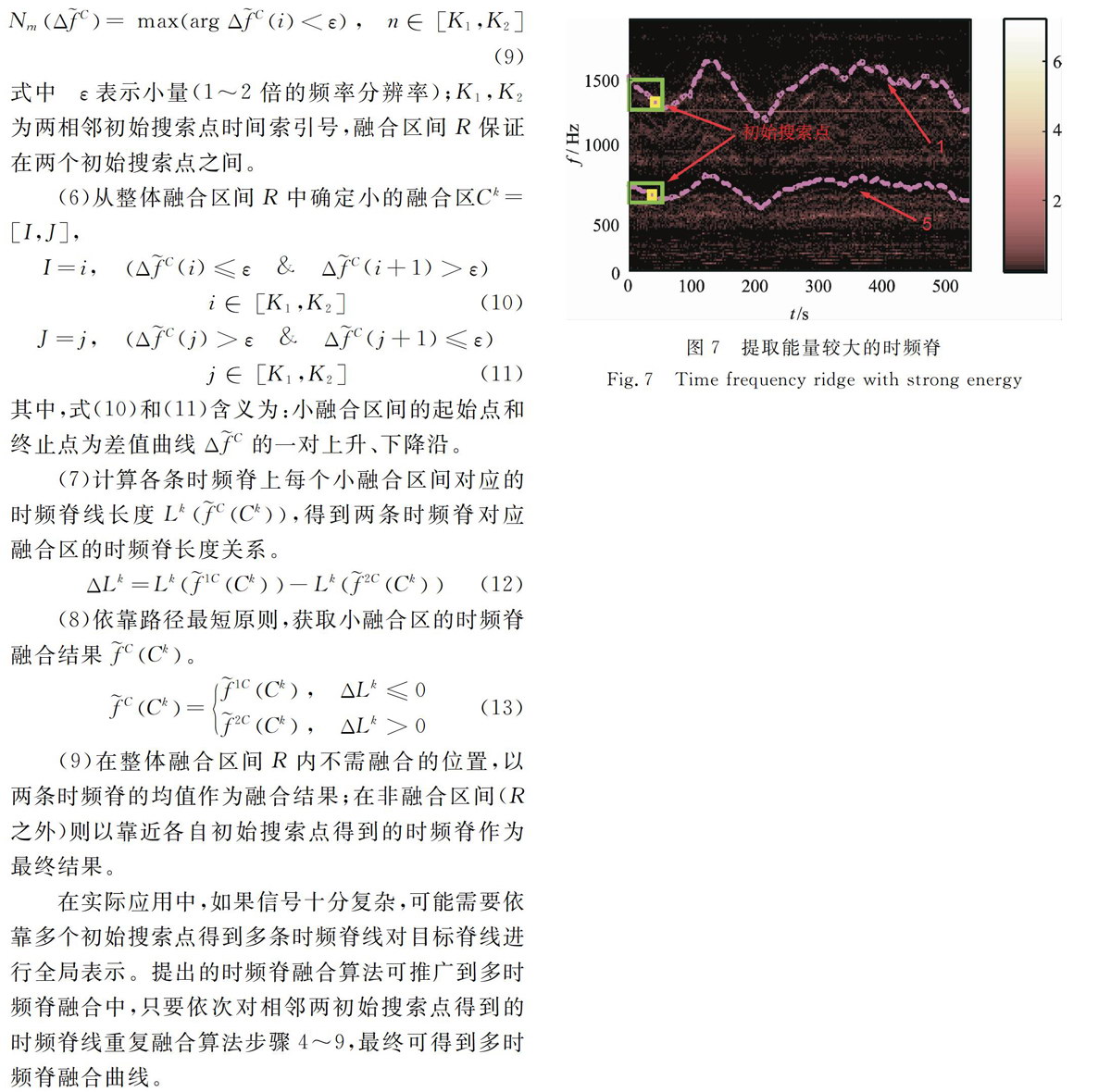
针对“挑战”行星齿轮箱振动信号中能量较大的分量提取,首先利用式(2)设定一个初始搜索点(确定初始搜索点位置时,局部时频矩阵只要大致包含待提取脊线即可)。如果待提取脊线能量较大,一般单一代价函数可以识别出时频脊。以时频图4中箭头1和5指示能量较大的时频脊提取为例,如图7所示在信号前50s选择图所示矩形框位置为局部时频矩阵区间,确定各自初始搜索点为P1(43s,1338Hz),P5(38s,592Hz)),然后利用融合方法步骤3中的代价函数提取到图中粗虚线所示时频脊线。本文搜索半带宽fw设置为20Hz,虽然搜索带宽固定,但搜索频率范围是随着当前搜索脊点的前或后一时刻已确定的频率点值而动态变化。因此半带宽值不用过大,甚至过大的半带宽反而会因时频脊附近的强噪声干扰带来较大的误差,而较小的半带宽亦可提高计算效率。因图4中箭头1指示的能量较大时频脊与箭头2指示的固定频率成分相交,所以在提取箭头1指示的时频脊之前需将箭头2指示分量去除。另外,在提取一些能量较弱的时频脊时,也需要将其临近的一些能量较大的时频脊分量先去除,防止对能量较弱的时频脊提取造成干扰。考虑到信号时频变换后,各分量存在一定的带宽,但脊线提取的代价函数中含频率变化率约束项,所以只要去除相邻脊线能量较大的频率点即可,一般在能量较大的时频脊线上、下去除3~4倍频率分辨率的带宽成分。
同样,针箭头4指示的能量较弱脊线(前述分析表明其为高速轴齿轮啮合频率曲线)的提取,在图8所示信号两端包含目标脊线的局部区域(图中矩形框位置)确定两初始搜索点P41(40s,676Hz),P42(543s,631Hz)。再利用时频脊融合法步骤3中代价函数搜索时频脊。图8中可以很直观地看出两初始搜索点对应的时频脊线在两端出现突变,单一时频脊线难以表示目标脊线。此外,图9所示提取脊线的中间局部放大位置也存在一些不重合区问。
为解决上述目标脊线提取失效的问题,采用提出的时频脊融合方法。其中,在融合过程中对如图8所示的两条时频脊线进行差值,得到图10所示差值曲线;再通过差值曲线的信息,确定整体时频脊融合区间(图中两方形点位置)。然后,在整体融合区间内依次查找小融合区。可从图10中间局部放大位置看出整体融合区间中存在非常多的小融合区域(图中峰值位置);最后获取到完整的时频脊融合结果。根据高速轴齿轮的齿数,可将提取时频脊转化为图11所示高速轴转速曲线。
时频脊融合方法得到的高速轴转速与初步分析得出其大部分运行转速在1550~1800r/min之间相吻合。为进一步说明提出方法的有效性,利用模极大值脊线提取框架和单一代价函数分析实验信号得到高速轴转速,对比各方法转速提取的结果可知模极大值法在初始阶段存在局部波动,然后出现发散,最后收敛于箭头5指示的能量较大时频脊;单一代价函数在中间位置存在局部波动,最后阶段也出现发散现象。为进一步评价转速提取的精确性,下节将利用提取转速信息将原始信号变为角度域信号,然后观察信号的阶次谱。如果能够清晰地检测到各齿轮对啮合频率及其倍频对应的阶次,也可说明提取的转速有效。
3.2时频脊融合方法提取转速的准确性验证
阶次分析是以参考轴转速作为参照,对原始信号进行角度域重采样(角度域采样点数与原始采样点一致,保证阶次的分辨率),可将非平稳信号变换为平稳信号。图12是以时频脊融合方法得到的高速轴转速作为参照进行角度域变换后信号的时频图,图中出现了许多平稳分量。箭头4指示的一条平直线为高速轴齿轮啮合频率脊线。与图4中箭头4指示的时频脊线对比,可知利用提取转速信号进行重采样,得到了平稳信号,说明提取转速的有效性與精确性。
另外,对照原始信号频谱图3和阶次谱图13,可知阶次谱图中峰值多且显著。为了进一步验证提取转速的有效性,下面检测阶次谱中各峰值能否与齿轮箱各齿轮对啮合频率一一对应。
通过表1,2的参数以及式(19)计算得到行星轮轴承内圈故障频率fBPF1,对应的阶次为0.1909。图17为阶次谱的局部放大。图18光标显示了3,4倍的行星轮轴承内圈故障频率fBPF1对应的两个阶次的位置。对照图17和18可清楚地检测到3,4倍的行星轮轴承内圈故障频率fBPF1对应的两个阶次频率加上行星架转频f1的调制之后,频率3fBPF1±f1和4fBPF1±f1对应的阶次位置存在明显的峰值,所以可以确认三个行星轮轴承中有一轴承内圈出现了 故障。
5.结论
(1)提出的时频脊融合方法解决了一般时频脊提取方法易受信号幅值变化、噪声等因素干扰引起的时频脊线提取失效的问题。同时,时频脊融合方法推广到多时频脊融合中,可进一步解决更加复杂的振动信号中弱能量时频脊提取的问题。
(2)与两种现有脊线提取方法对比可知,提出的时频脊融合方法在跟踪脊线时更加可靠。另外,在角度域信号的阶次谱中清晰地检测到了各齿轮对啮合频率及其倍频的对应阶次,也证明了提出的时频脊融合方法提取高速轴转速的准确性。
(3)从试验信号的阶次谱中观察到了行星轮轴承内圈故障特征频率,实现故障诊断。同时也验证了推导出的行星轮轴承故障频率计算式的正确性。该计算式为行星轮轴承故障诊断提供了依据。
(4)本文针对实际工程中的行星齿轮箱振动信号处理(信号采样时间长),直接采用短时傅里叶变换,再利用时频脊融合方法提取转速,最后通过阶次谱识别出轴承故障位置的处理技术,具有计算效率高的特点,非常适合于工程应用。致谢
感谢法国里昂大学提供的行星齿轮箱“挑战”机会和Maia Eolis公司无私贡献行星齿轮箱振动信号,以及审稿专家和编辑的宝贵建议。

