多智能体的振动噪声前馈主动控制技术
崔怀峰 胡如夫 陈南
摘要:传统振动噪声主动控制系统在灵活性、通用性和稳定性等方面存在缺陷,难以适应外界环境的动态性和不确定性。由此考虑将多智能体技术与经典的控制理论自适应前馈FxLMS控制算法综合起来形成有效智能控制系统。根据主导振动噪声的结构模态分解振动噪声控制问题,比较结构特征频率声压和一预设阈值大小来定义控制器操作域。综合各种功能函数和自适应FxLMS算法形成控制单元(控制器智能体)。通过最大声压频率和特征频率之差小于某一常数a来定义决策函数,以决策各控制单元的优先启动。提取传递函数至上层组织作为加权系数以实现各控制单元之间的合作。通过调整常数a能够实现不同控制器的灵活启动,并利用智能体之间的合作实现系统的通用性和稳定性。
关键词:振动噪声;前馈主动控制;多智能体技术;智能控制
中图分类号:TB535;TB532
文献标志码:A
文章编号:1004-4523(2017)01-0062-09
DOI:10.16385/j.cnki.issn.1004-4523.2017.01.009
引言
与振动噪声主动控制发展的长久历史、人力物力的大量投入相比,主动控制技术的实用化进程目前还没达到人们最初的预期,主要原因是很多研究成功的主动控制系统在稳定性、通用性、安装维护便利性等方面存在某一项或几项缺点,严重制约了它们的推广应用。由此考虑综合多智能体技术与自适应前馈算法建立振动噪声主动控制系统,以期解决上述难题,实现以车厢、机舱等为研究背景的复杂封闭空间智能降噪。
智能体能在特定环境下感知环境,并能自治地运行以代表其设计者或使用者实现一系列目标的实体或计算程序。智能体具有自治性、主动性和社会性等特性,被看成是多智能体系统的微观层次,可以实施要求一定“智商”的特定的功能;而有关智能体问的关系研究则构成多智能体系统的宏观层次,其特点在于通过对各层次智能体的组织与协作,完成那些需要更高灵活性、环境适应性以及柔性的综合功能。目前基于多智能体的控制技术正受到控制学术界和工程应用界极大关注。
在振动噪声控制研究领域中,控制算法是至关重要的。有源声控制普遍采用自适应前馈FxLMS(Filtered-x Least Mean Square,x滤波最小均方)算法,并且基于此算法的产品已推向市场。振动噪声主动控制大多也采用该算法。它的缺点是鲁棒性差、对控制通道误差敏感,因此对它的性能分析和改进一直是热点问题。同时,由于复杂结构与声场耦合导致的高维动态系统、恶劣变化的环境、问接传感机制以及尚不完善的建模工具所必然导致的物理模型不确定性等诸多因素的影响,使得控制系统的通用性和稳定性成为其能否应用于实践的关键因素。目前,振动噪声主动控制领域用到的算法还有:鲁棒H∞控制理论、遗传算法等,但需要克服它们计算量大、实时性差等缺点。本文综合自适应前馈FxLMS控制算法及其智能体的智能应激反应算法形成控制器的核心软件部分,以解决不确定性干扰导致的系统自适应和稳定性等问题。另外,智能体的模块化及其控制框架的设计可实现系统的强可扩展性。
目前传统振动噪声主动控制大多是在整体系统单一层次进行建模,尽管这种方法设计思路简单明确,但对复杂高维耦合连续分布参数结构系统,实践证明其控制效果并不理想。同时,系统大多采用分布式控制,导致其难以大规模工程应用。因为系统中各控制单元尽管有共同的控制目标,但缺乏交流与合作的灵活性,难以适应复杂耦合系统的稳定状态对随机干扰的敏感性。因此如何解决控制单元和整体控制架构之间的冲突与协调问题成为关键技术。针对复杂耦合系统,国际最新的技术趋势是分布控制若干“机敏单元”,实现对高维耦合系统的动力学特征或过程的控制。本文研究符合这一趋势,提出基于多智能体的振动噪声主动控制技术。智能体之间能够交互的复杂模式适合解决分布式控制问题,尤其适合控制和求解数据等在本质上是分布式的问题,并能够提供高稳定性和高效率的解决方法。
综上所述,针对高维耦合分布参数复杂结构系统,应不再遵循传统主动控制只在整体单一层次建模分析并设计控制系统的思路,在控制逻辑和设计方法上,将多智能体理论和自适应控制算法有机结合起来以解决复杂分布式振动噪声控制问题,追求使系统具有更好自适应能力和稳定性,真正使振动噪声主动控制对复杂结构系统成为可行并应用于工程实践。
1.声场模型
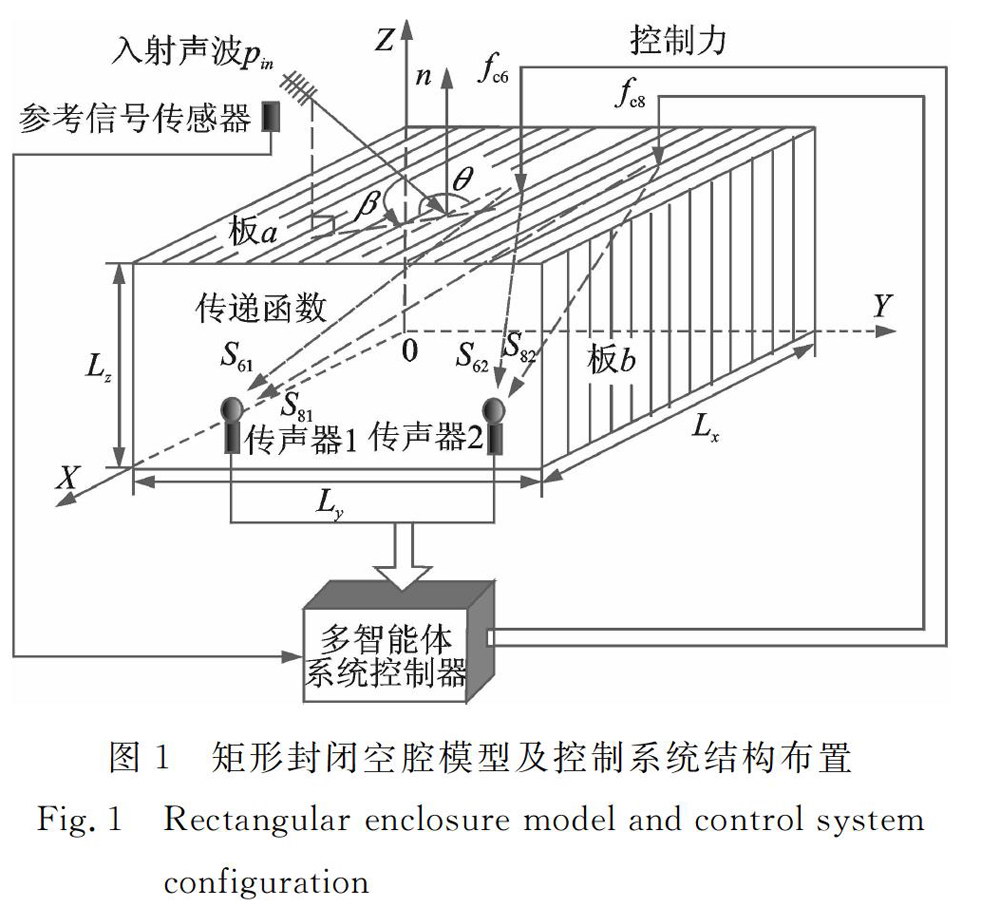
国内外研究人员在分析封闭空腔内声场时,大多选取全刚性壁或最多只含一块弹性壁的封闭空腔作为研究对象,但现实生活中的封闭空腔,比如车厢、机舱等都是由多块弹性壁组成。为了更好模拟实际封闭空腔的声场,本文选取声场模型为由2块简支撑弹性板和4块刚性板组成的矩形封闭空腔,如图1所示。考虑弹性板的简支撑边界条件是因为一个简支撑矩形板比较接近许多实际结构的状态。两弹性板分别被标记为板a和板6,其所在位置坐标分别为x=Lz=Lx和y=Ly彈性板均假设为各向同性。矩形腔的长、宽、高分别为0.868,1.15,1.0m。弹性板均为铝板,其弹性模量E=71GPa,质量密度p1=2700kg/m3,泊松比u=0.3。铝板厚度主要对结构模态产生影响,当结构模态变化时腔内主导振动噪声会随之变化。本文方法具有一定通用性和可扩展性,易于解决此类情况,故板a和板6的厚度不妨均取6mm。声速为c=344m/s,空气的质量密度p=1.21kg/m3。
一外部声场作用在板a上,使得板a向腔内辐射振动噪声。外部声场假设为一平面波Pin,入射角度为β=45°(与水平面之间的夹角)和θ=135°(与z轴之问的夹角)。假定空腔外部入射声波和辐射声波之问的干涉忽略不计。分布控制力fci(i=1,…,L)也施加在板a上,以有效抑制板a的声辐射。本文声场模型与参考文献中的声场模型相比,初级干扰仅考虑外声源激励,即声场建模只需将参考文献[23]中的干扰点力(初级激励之一)忽略即可,为简洁起见不再推导。
2.基于多智能体的振动噪聲控制系统
2.1振动噪声控制问题分解
封闭空腔内振动噪声由受到初级激励的弹性板的结构模态和空腔的声模态所主导,尤其是当弹性板和空腔的特征频率接近时将产生强烈的结构声耦合,导致腔内声压在该频率上出现峰值。当封闭空腔尺寸不是很大时,腔内振动噪声主要由几阶结构模态所主导,如果控制了这几阶结构模态,即可实现显著降噪。由此考虑将封闭空腔结构声控制问题按照对封闭空腔声场贡献较大的几阶结构模态将其分为若干子控制问题。
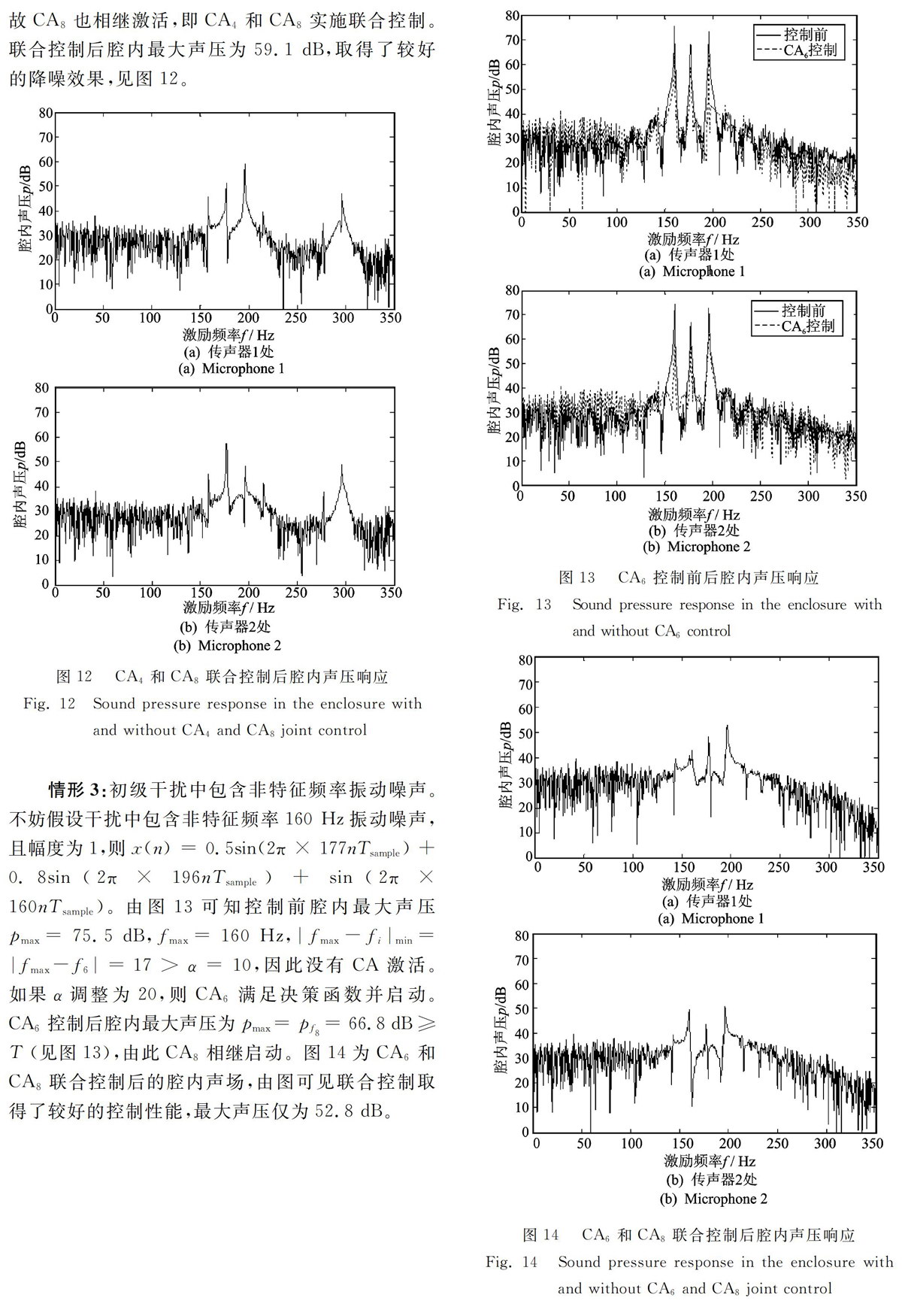
下面首先给出在外声源作用下的腔内初级耦合声场,如图2所示。由图2和表1可知,板a的第1(30Hz),4(119Hz),6(177Hz),7(186Hz),8(196Hz),9(219Hz),10(255Hz)阶模态对腔内声场贡献较大,不妨以板盘的第6和第8阶模态为例,将腔内振动噪声控制问题分解为针对板a第6和第8阶模态振动噪声的两个子控制问题,并分别表示为CA。(控制器智能体6,Controller Agent6)和CA8(控制器智能体8,Controller Agent8)。
2.2子控制问题求解
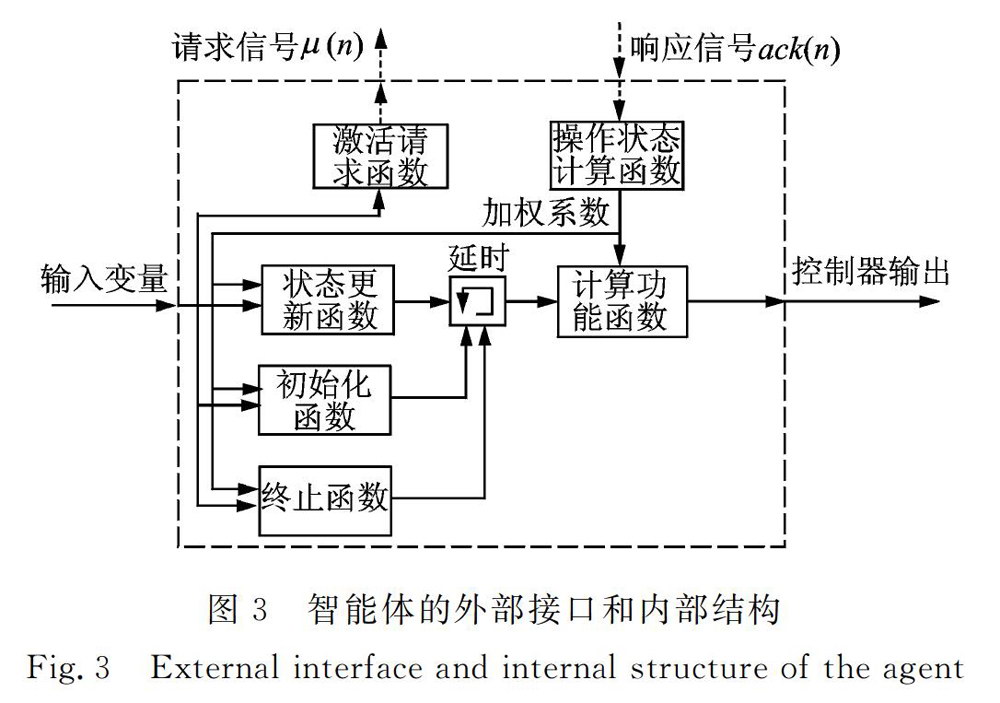
子控制问题的解决方案由控制器智能体来执行。控制器智能体包括外部接口和内部结构。它的外部接口是由输入、输出、激活请求信号和应答信号接口组成,如图3所示。输入接口用于接收传感器信号,输出接口用于发送控制电压信号给点力致动器。激活请求信号(表示为u(n))和应答信号(表示为ack(n)接口用于协调与系统中其他的控制器智能体之问的行为关系。其中,n表示离散时间序列。
控制器智能体的内部结构由用于实现其功能行为的函数组成,主要包括激活请求函数、计算功能函数和操作状态计算函数等。下面具体讨论各个函数的功能和定义。
首先,激活请求函数用来定义控制器智能体的操作域和计算激活请求信号,并发送给上层组织(协调对象结构)。激活请求函数定义为
Pfi≥T, i=6,8(1)式中i为板a的模态阶数,fi为板a的第i阶模态所对应的特征频率,pfi为特征频率fi上的腔内声压,rf为振动噪声标准阈值。如果满足激活条件(1),则控制器智能体被激活并向上层组织发送二进制激活请求信号u(n)(=1),然后上层组织通过协调机制处理激活请求信号,并发送响应信号以决定控制器智能体操作状态是激活还是保持不激活。
计算功能函数的作用是根据控制算法获得期望的控制信号或控制行为。计算功能函数中的控制算法采用自适应前馈FxLMS算法,其控制框图如图4所示。图中相关符号的含义分别为:P(z)为初级通道传递函数;s(z)为次级通道传递函数;S(z)为次级通道传递函数的估计;w(z)为自适应滤波器,线性预测初级振动噪声以最小化残留噪声;z(n)为y(n)经过S(z)滤波输出信号和声压误差信号e(n)合成的参考信号;z(n)为z(n)经S(z)滤波得到的信号,称为滤波-x信号;e(n)为传声器测得的声压误差信号;d(n)为初级激励在传声器处产生的声压信号,即初级振动噪声;s(n)为次级源在传声器处产生的声压信号;y(n)为自适应滤波器生成的次级电压信号,用于驱动点力致动器。在仿真中,P(2),S(z),S(x)和w(x)均利用有限脉冲响应(FIR)滤波器进行建模。图5为计算功能函数模块的外部接口和内部结构。
操作状态计算函数用于识别来自协调对象的应答信号,当应答信号ack(n)从0变为1时,控制器智能体执行初始化函数,反之执行终止函数,实现智能体在激活和禁止状态之问的转换。更新函数用于更新系统内部的状态变量。
CA之问的合作是通过协调对象向其发送相应的加权系数来实现。因为CA控制行为之问的耦合表现为相互间的传递函数,故将传递函数提取出来储存在协调对象中作为加权系数。通过协调对象结构将各CA组织成振动噪声主动控制系统,如图7所示。整个系统控制流程如图8所示。因为有两个传声器,故激活请求函数中的pfi由较大声压的传声器得到,协调对象中的最大声压同样如此。
4.结论
传统主动控制系统尤其是多通道控制系统在动态干扰环境下缺乏灵活性、社会性和自治性等智能属性,难以满足工程应用中所需系统的强稳定性和通用性。本文将多智能体技术与自适应FxLMs算法综合起来建立智能控制系统,并通过仿真得到以下结论:
(1)针对不同频率振动噪声,调整决策函数中的常数a以启动相应的控制器,实现灵活降噪,并使控制系统平稳运行。
(2)将传递函数作为加权系数设计控制器之问的合作机制,使控制单元易于添加或移除,提高了系统的通用性。
(3)传统主动控制系统具有一定自适应性和较好的降噪水平,在此基础上综合多智能体技术使控制单元能够自治并相互交流(社会性),实现智能降噪技术以取得更佳降噪效果。

