变温度场中刚柔耦合功能梯度梁系统的动力学特性研究
黎亮 章定国 郭永彬


摘要:基于刚柔耦合动力学和热力学建模理论,研究变温度场环境下的旋转柔性功能梯度梁系统的动力学问题。功能梯度梁由陶瓷和金属两种材料组成,假设梁的典型物性参数为梁厚度方向坐标的幂函数。设计两种材料梯度分布规律,考虑功能梯度梁上任意位置附着集中质量,在梁纵向位移中计及由于横向变形而引起的纵向缩短项,即非线性耦合变形量。考虑温度梯度变化对系统动力学特性的影响,求解得到功能梯度梁沿厚度方向分布的温度场,在功能梯度梁本构关系式中计及热应变。采用假设模态法描述变形,运用第二类Lagrange方程推导得到系统的刚柔耦合动力学方程。仿真结果表明,集中质量位置和材料梯度分布规律的选取都将对系统动力学特性产生重大影响,第二种梯度分布规律下的功能梯度梁抗热载荷冲击性能优于第一种梯度分布规律下的功能梯度梁。
关键词:多体动力学;功能梯度材料梁;刚柔耦合;温度场
中图分类号:0313.7;0322
文献标志码:A
文章编号:1004-4523(2017)01-0009-11
DOI:10.16385/i.cnki.issn.1004-4523.2017.01.002
引言
在航空航天领域中,结构的运动部件往往在高温、高载的严酷工况下经历大范围运动,这使得航天器结构设计成为一个复杂、多学科交叉的问题。为满足各种复杂工况,既保证结构耐高温高热又不影响结构的强度特性,需要设计出新型功能复合材料并建立相应复合结构的多物理场耦合动力学模型。
中心刚体一柔性梁系统是一类具有代表性的刚柔耦合系统简化模型,有关该模型的动力学建模方法的研究以及刚柔耦合问题的研究工作已经日臻完善。近年来,学者们已经开始关注考虑热效应的热耦合动力学问题,并将上述研究工作推广至温度场下的柔性多体系统。刘锦阳和洪嘉振采用假设模态法针对温度场下做大范围运动的柔性梁刚柔耦合系统建立了一次近似耦合动力学模型,在本构关系式中计及热应变,研究了低速转动工况下柔性梁系统动力学的几何非线性效应。刘锦阳等建立了带中心刚体柔性曲梁的刚柔耦合模型,该模型结合了混合坐标法和绝对坐标法的特点,基于小变形假设,在应变能中计及热应变,研究了温度变化引起的曲梁的热膨胀对系统动力学性态的影响。刘锦阳和崔麟采用虚功原理建立了适用于求解大变形问题的热载荷作用的柔性梁的热传导方程和旋转刚体一梁系统的刚柔耦合动力学方程,研究了热流引起的温度梯度对弹性变形和刚体转动的影响及大变形情形下的几何非线性效应。魏麟欢等利用一次近似耦合模型理论,采用广义Ham-ilton原理推导得到了中心刚体一楔形梁一质点系统的动力学模型,研究了考虑热冲击效应的系统动力学响应规律。上述研究工作的研究对象都是局限于传统均质材料柔性梁刚柔耦合系统,尚未推广到应用日益广泛的先进功能型复合材料梁刚柔耦合系统。文献[18-20]关注并研究了含功能梯度材料(Func-tionally Graded Materials,FGM)的旋转刚柔耦合系统的动力学特性,但相关的研究侧重于系统动力学建模方法推广,忽略了对FGM结构在实际温度梯度环境下工作的动力学特性的分析。Oh等率先开展了温度场下旋转功能梯度材料涡轮机叶片的振动特性研究,但其研究工作忽略了对系统刚柔耦合动力学特性的分析。目前,考虑温度场效应的功能梯度材料复合结构的研究并不完善,尚未建立基于热力学和刚柔耦合动力学理论的功能梯度材料结构的热刚柔耦合动力学模型。
本文以做大范围旋转运动的中心刚体-FGM梁一集中质量系统为研究对象,基于高次刚柔耦合动力学理论和热力学理论进行动力学建模,推导获得变温度场环境下的旋转柔性FGM梁系统的动力学方程。所考虑的变温度场随空间变化而不随时间变化。假设FGM梁的各项物理特性沿着梁厚度方向按两种不同幂律规律分布,通过泰勒级数展开法求解得到相应的梯度变温度场。通过数值仿真算例研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性。
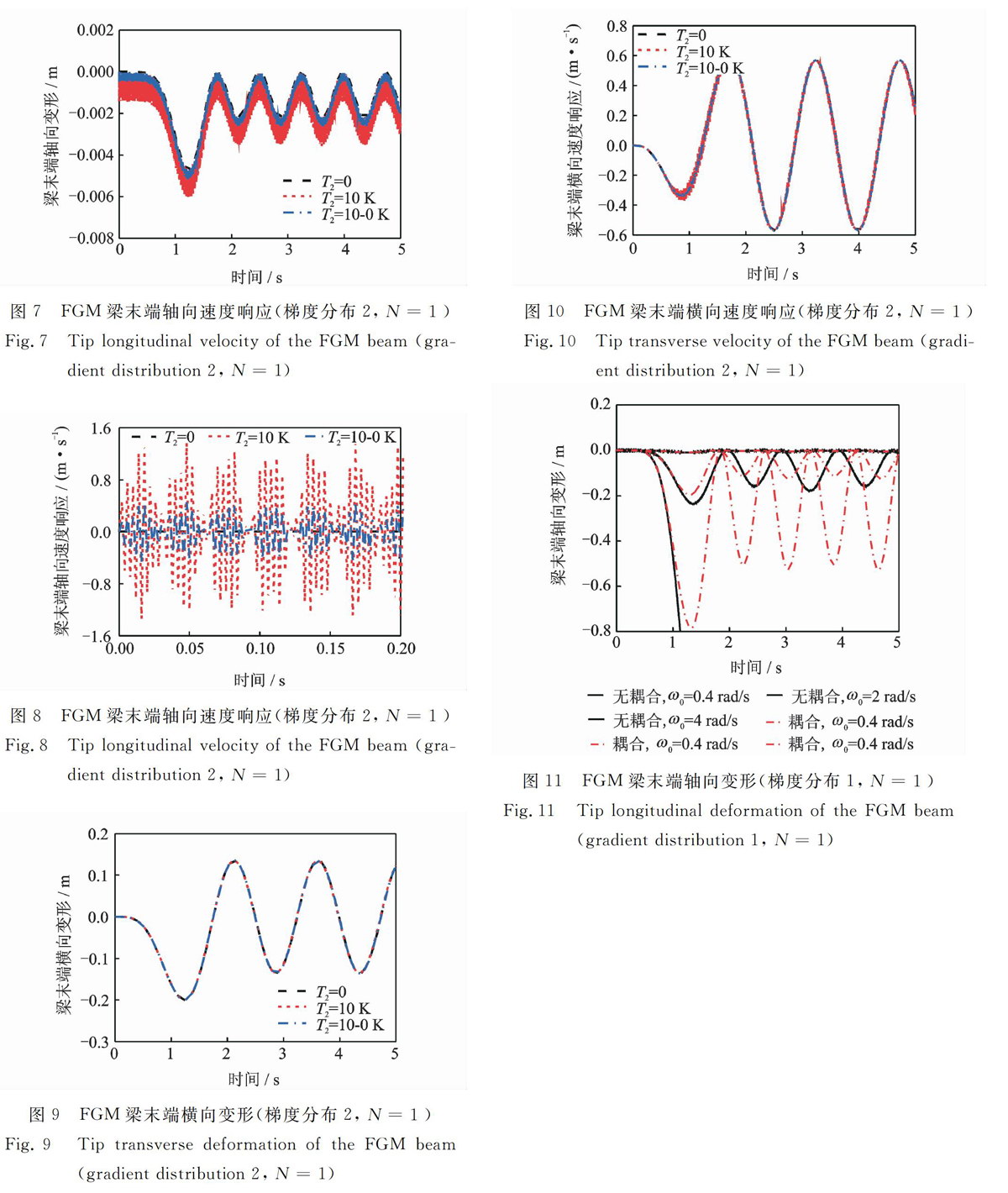
图7和8分别给出了梯度分布2(N=1),三种温度场环境下FGM梁末端轴向变形图和轴向速度响应图。比较图3和7可知,同等温度载荷作用下,梯度分布2的FGM梁末端的轴向变形幅值小于梯度分布1的,其轴向变形的振荡现象较梯度分布1的FGM梁的更为平稳。比较图4和8发现,两种FGM梁末端的轴向速度响应相差不大。图9和10分别为梯度分布2(N=1),三种温度场环境下FGM梁末端横向变形图和横向速度响应图。从图9可以看出,无论是受恒温度载荷还是梯度变温度载荷作用,梯度分布2的FGM梁末端横向变形均与未受热载荷时的横向变形曲线基本重合。图10中,受热载荷作用的FGM梁的横向速度响应除了在大范围运动角速度展开过程中有较为明显的振荡外,在稳态匀速转动过程中已经无明显振荡,且与不考虑热载荷作用的无振荡速度曲线基本重合。比较图5和9以及图6和10可以发现,同等温度载荷作用下,梯度分布2的FGM梁末端的横向变形幅值和横向速度响应幅值均小于梯度分布1的FGM梁的横向变形幅值和横向速度响应幅值,后者速度响应的振荡幅度明显高于前者。由此可见,同等几何参数下的两种FGM梁,在保持相同体积分数指数及质量的前提下,梯度分布2的FGM梁的抗热冲击载荷性能大大优于梯度分布1的FGM梁。
图11和12分别给出了不考虑非线性耦合变形量与考虑非线性耦合变形量情形下FGM梁末端轴向变形和横向变形响应情况。显然,随着。的增大,无耦合模型计算结果趋于发散,而耦合模型计算结果仍保持收敛,说明本文模型具有更广泛适用性,其计算结果精度更高。
图13和14分别给出了温度场下两种FGM梁(N=0.5)末端軸向及横向变形响应随着集中质量位置变化的影响情况。从图中可以看到,FGM梁的变形响应幅值随着集中质量位置趋向梁末端而逐渐增大。温度场对梯度分布1的FGM梁的动力学响应的影响明显强于对梯度分布2的FGM梁的影响。
3.2系统大范围运动未知
研究外部驱动力对中心刚体FGM梁一集中质量系统的动力学特性的影响,此时系统的大范围运动规律是未知的。设作用在中心刚体上的驱动力矩为Fr=5exp(-120t),系统物理参数与上一小节相同,仍然考虑上述三种温度场环境。
图15(a)和(b)分别给出了受温度场影响,梯度分布1情况计算得到的中心刚体的角位移与角速度响应图。从图中可以看出,热载荷也会导致中心刚体的大范围角位移产生高频振荡,梯度变温度场(T1=10-OK)下刚体位移、速度响应要比恒定温度场(T1=10K)的偏小且更加稳定。图16(a)~(d)分别给出了梯度分布1情况下FGM梁末端的变形与速度响应图。显然,梁末端的轴向和横向变形均能观察到热致振荡现象。图17(a)和(b)分别给出了受温度场影响,梯度分布2情况计算得到的中心刚体的角位移与角速度响应图。图18(a)~(d)分别给出了梯度分布2情况下FGM梁末端的变形与速度响应图。分别对比两种梯度分布情况下系统动力学响应图,第2种分布情况下相应的刚体部件和柔性梁附件的位移(变形)响应幅值均远远小于第1种分布情况,而相应的速度响应却相差不大。
4.结论
本文建立了中心刚体-FGM梁一集中质量系统在变温度场作用下的动力学方程,研究了温度载荷对大范围运动已知和未知情形下的系统动力学特性的影响,得到如下结论:
(1)大范围运动已知情形,当FGM梁受热载荷冲击时,其末端轴向变形和速度响应均呈现高频振荡。温度场对FGM梁横向变形的影响较对轴向变形的影响偏弱。FGM梁的变形响应幅值随着集中质量位置趋向梁末端而逐渐增大。由于非线性耦合变形量的计人,系统动力学响应在大范围转速为高速情况下的数值计算结果较无耦合模型的结果更为精确。
(2)大范围运动未知情形,梁末端的轴向和横向变形均能明显观察到热致振荡现象,热载荷也会导致中心刚体的大范围角位移产生高频振荡。
(3)同等几何参数下的两种FGM梁,在保持相同体积分数指数及质量的前提下,梯度分布2的FGM梁的抗热冲击载荷性能大大优于梯度分布1的FGM梁。
(4)梯度变温度场对系统动力学响应的影响要弱于恒定溫度场,热载荷导致的振荡现象可通过设计柔性FGM梁的材料梯度分布规律得到一定程度抑制。

