基于韦伯模式的中考数学试题与课程标准的一致性研究

    吴晓红 莫宗赵 周莹

    

    

    

    【摘 要】 近年来，中考试题与课程标准的一致性成为学业评价领域的热点课题.基于本土化的韦伯模式，从知识种类、知识深度、知识广度、知识分布平衡性一致性四个维度，对2019年桂林、贵港两地中考试卷与课程标准一致性进行研究.研究结果表明：第一，两份试卷在各维度一致性整体上良好;第二，两份试卷在各学习领域与课程标准的一致性水平表现不一.未来中考命题要更加重视课程标准，确保中考试题与课程标准的高度一致性，尤其是要适当地提高知识的考查广度，降低部分考查内容的难度

    【关键词】 中考数学试题;课程标准;韦伯模式;一致性

    《基础教育课程改革纲要（试行）》指出：国家课程标准是教材编写、教学、评估和考试命题的依据，是国家管理和评价课程的基础[1].《教育部关于积极推进中小学评价与考试制度改革的通知》也指出：初中毕业、升学考试命题必须要依据国家课程标准[2].中考作为义务教育阶段的终结性考试，其具有“牵制教育目的、引导教育过程和评价教育结果”等功能[3].因此，中考数学试卷与课程标准（《义务教育数学课程标准（2011年版）》）的一致性水平，不仅直接关系到数学试题的质量，还关系到课程标准在教学中的落实.通过查阅文献发现，尽管近年来对中考数学试卷与课程标准一致性研究广受关注，但鲜有研究者对广西地区的中考数学试卷与课程标准进行研究.鉴于此，本研究以2019年桂林、贵港两地中考数学试卷为研究样本，研究中考数学试卷与课程标准的一致性，以期为中考数学命题提供参考和借鉴，促进课程标准在教学中更好地落实.

    1 研究对象与工具

    1.1 研究对象

    本研究以2011年教育部颁布的《义务教育数学课程标准（2011年版）》（以下简称“课程标准”）和2019年桂林、贵港两地中考数学试卷为研究对象.

    1.2 研究工具

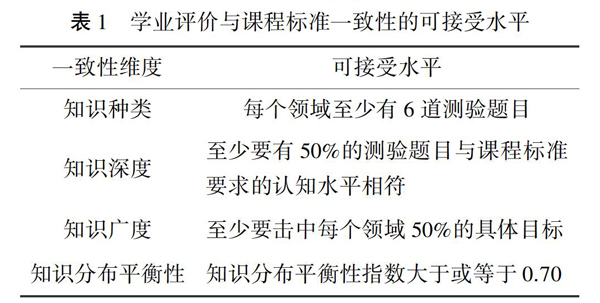
    “一致性分析范式”是指判定和分析课程系统各相关要素吻合程度的理念、程序与方法的总和.目前，国内外用于一致性研究的模式主要有韦伯模式（Webb?Model）、“SEC”模式（Surveys?of?Enacted?Curriculum?Model）、成功模式（Achieve?Inc.Model）等.本研究采用韦伯模式为研究工具，分析中考数学试题与课程标准的一致性水平状况.韦伯模式的一致性可接受水平判断标准如表1所示

    2 研究过程

    2.1 韦伯模式的本土化

    2.1.1 知识深度水平的划分

    韦伯模式的知识深度划分为回忆、技能或概念、策略性思维、拓展性思维四个层级，考虑到中国与美国在课程标准等方面存在着差异，而中考是对学习结果的评价，故按我国课程标准中的结果性目标进行编码，将知识深度水平划分为四个层级：了解、理解、掌握、运用.

    2.1.2 课程标准目标层次划分

    韦伯指出，课程标准的内容目标呈现“金字塔”式的层级体系，金字塔的顶部是“学习领域”，金字塔的中部是“主题”，即学习领域的下级目标，金字塔的底部是“具体目标”，即主题的下级目标.课程标准把课程内容划分为四个部分：数与代数、图形与几何、统计与概率、综合与实践[4].为了将课程内容进一步细化分析，结合初中数学知识内容的划分特点和“综合与实践”内容不适合在中考数学试卷中考查等情况，在参考徐帆[5]、周莹[6]等人的研究基础上，将课程标准的课程内容划分为七个学习领域：数与式、方程与不等式、函数、图形的性质、图形的变化、图形与坐标、统计与概率.

    2.2 研究对象的编码

    2.2.1 课程标准的编码

    基于韦伯模式的理念，对课程标准进行编码.首先，对课程标准的七大学习领域数与式、方程与不等式、函数、图形的性质、图形的变化、图形与坐标、统计与概率依次编码为1，2，3，4，5，6，7;其次，对每个学习领域下的主题进行编码为1.1，1.2，1.3，1.4，…最后，对具体目标进行编码为1.1.1，1.1.2，1.1.3，…此外，在编码过程中如果某一具体目标出现多个行为动词或者多个短语时，需要进行拆分编码;如果某一具体目标有两个层次的认知水平行为动词，则按照认知水平高的行为动词进行编码.按照以上的编码原则，将课程标准中的具体目标共编码为378个.其中，“数与式”包含4个主题，73个具体目标;“方程与不等式”包含2个主题，20个具体目标;“函数”包含4个主题，35个具体目标;“图形的性质”包含7个主题，161个具体目标;“图形的变化”包含5个主题，50个具体目标;“图形与坐标”包含2个主题，14个具体目标;“统计与概率”包含2个主题，25个具体目标.

    2.2.2 中考试题的编码

    首先，对试题及解答过程进行分步，分析每一步考查的知识点及其认知水平;然后，参照课程标准的编码表找到对应的具体目标，对试题进行编码;同时，对具体目标的实际考查水平与课程标准的要求进行比较，若考察知识点水平高于课程标准的要求，则记为“A”，相符记为“B”，低于记为“C”.试题编码以2019年贵港市中考数学试卷第1题为例：

    【例】1.计算（-1）3的结果是（）.

    A.-1B.1C.-3D.3

    本题考查有理数的乘方运算.通过对照课程标准编码表，考查的知识点对应“1.1.14掌握有理数的乘方运算”的具体目标，要求的认知水平为“掌握”.在解决这道题目时，学生需要掌握有理数乘方的运算法则，考察知识点的认知水平与课程标准的要求是相符，所以编码为“1.1.14?B”.

    3 研究结果及分析

    3.1 知识种类一致性分析

    知识种类一致性标准是用来判断评价项目涉及的内容主题范畴与课程内容标准中描述的内容主题范畴是否是一致的[7].由表2可知，在“图形的性质”领域下击中具体目标的题目数最高，桂林卷达到74个，贵港卷则达到了110个;在“数与式”学习领域击中的目标数次之，分别击中了51个、45个;在“图形的变化”学习领域下击中的目标数位于第三，分别击中了21个、27个;在“方程与不等式”“图形与坐标”“统计与概率”三个学习领域下击中具体目标的题目数依次减少，桂林卷在“統计与概率”学习领域下击中的题目数最少，击中量为9个，但也达到了可接受水平.从总体来看，2019年桂林、贵港两地的中考数学试卷在七大学习领域中击中具体目标的题目数都达到了6个以上.根据韦伯模式的可接受水平，两套试卷在七大学习领域与课程标准的知识种类一致性较好.

    3.2 知识深度一致性分析

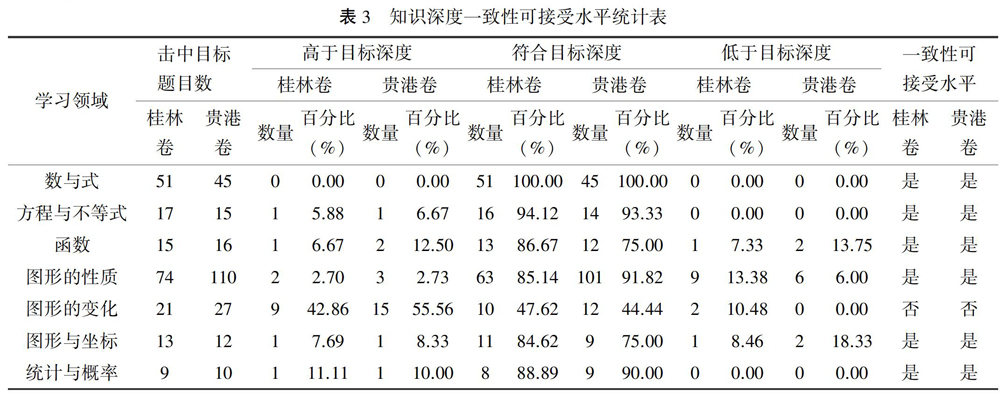
    知识深度的一致性标准被用来判断所评价的认知要求与内容标准中期望学生“应当知道什么”的目标是否相一致[8].由表3可知，两套试卷在“数与式”学习领域与课程标准的知识深度一致性水平最好，达到了100%，而在“图形的变化”学习领域与课程标准的知识深度一致性水平最不理想，分别是47.62%、44.44%.此外，两套试卷在“方程与不等式”“函数”“图形的性质”“图形与坐标”“统计与概率”五个学习领域与课程标准的知识深度一致性水平都较好，均达到了50%以上.根据韦伯模式的可接受水平，两套试卷在七大学习领域与课程标准的知识深度一致性较好.

    3.3 知识广度一致性分析

    知识广度的一致性标准被用来判断课程标准中所涉及的知识跨度与学生为了正确回答评价项目所需的知识跨度是否相一致[9]，即判断试卷考查的知识范围与课程标准要求掌握的知识范围是否一致.由表4可知，两套试卷在七大学习领域的知识广度在29%到51%之间，大部分学习领域的知识广度低于50%.按照韦伯模式的可接受水平为不少于50%的判断标准，两套试卷的知识广度一致性并不理想，只有在“方程与不等式”学习领域知识广度一致性都达到了可接受水平.而考虑到中考是在一定时间内完成一定量试题的考查，也就限定了题量，从而限定了知识考查的范围.因此，将知识广度一致性的可接受水平下调为40%，然而，两套试卷在“函数”“图形的性质”“图形的变化”学习领域知识广度一致性仍然未达到可接受水平.此外，桂林卷在“数与式”“图形与坐标”学习领域知识广度一致性达到可接受水平，在“统计与概率”学习领域知识广度一致性没有达到可接受水平;而贵港卷则是在“统计与概率”学习领域知识广度一致性达到可接受水平，在“数与式”“图形与坐标”学习领域知识广度一致性没有达到可接受水平.

    3.4 知识分布平衡性一致性分析

    知识分布平衡性是指考察各個测验题目在各项具体目标之间分布的均匀程度[10].知识分布平衡性指数是知识分布平衡度一致性的评价指标，它的计算公式为：

    知识分布平衡性指数=1-∑1O-IkH2.

    其中，O表示被命中领域的目标总数，Ik表示击中目标的试题数，H表示命中该领域的试题总数.若平衡性指数不低于0.7，则达到知识分布平衡性的可接受水平.由表5可知，2019年桂林、贵港两地的中考数学试卷在“图形与坐标”学习领域的平衡性指数分别是0.64、0.65，介于0.6到0.7之间，知识分布平衡性一致性没有达到可接受水平.而在其它六大学习领域的平衡性指数都达到了0.7以上，知识分布平衡性一致性均达到可接受水平，特别地，两套试卷在“统计与概率”学习领域知识平衡性表现出了最好的一致性，平衡性指数都达到了1

    4 结论与思考

    4.1 结论

    基于韦伯模式的2019年桂林、贵港两地中考数学试卷与课程标准一致性研究结果表明：第一，两份试卷在各维度一致性整体上良好.其中，“知识种类”“知识深度”“知识平衡性”三个维度与课程标准的一致性较好，而“知识广度”维度与课程标准一致性较差，这与中考试卷是以“限时限量”考查形式有关.第二，两份试卷在各学习领域与课程标准的一致性水平表现不一.桂林卷在“数与式”“方程与不等式”“图形与坐标”三个学习领域与课程标准的一致性较好，在“图形的变化”学习领域的一致性较差;贵港卷在“方程与不等式”“统计与概率”两个学习领域一致性较好，在“图形的变化”学习领域的一致性较差.

    4.2 思考

    鉴于在实际教学中，大部分教师把中考作为日常授课的“航标”，中考“考什么”、“怎么考”，教师就“教什么、“怎么教”，这就导致了一些中考不常考的知识点在教学中被忽略，而对反复考查的知识点倍受重视，把这些知识点当作教学的“重点”，这会影响学生知识结构的完整性.此外，部分知识点的考查难度远远超出了课程标准的认知要求，而教师为了提高学生的考试成绩，不得不在教学中人为地拔高这些知识点的学习难度，从而加重了学生的学习负担.因此，为了更好地发挥课程标准在教学中的主导作用，提高中考试卷与课程标准的一致性就显得尤为重要.因此，未来中考命题要更加重视课程标准，确保中考试题与课程标准的高度一致性，尤其是要适当地提高知识的考查广度，降低部分考查内容的难度

    参考文献

    [1]中华人民共和国教育部.基础教育课程改革纲要（试行）[M].北京：人民教育出版社，2001.

    [2]中华人民共和国教育部.教育部关于积极推进中小学评价与考试制度改革的通知[EB/OL].http：//www.moe.gov.cn/srcsite/A26/s7054/200212/t20021218_78509.html，2002-12-18.

    [3]郑若玲.论高考的教育功能[J].教育导刊，2005（1）：4-6.

    [4]义务教育数学课程标准（2011年版）[S].北京：北京师范大学出社，2012，3.

    [5]徐帆，张胜元，孙庆括.初中数学学业评价与课程标准的一致性研究——以福建省五套数学试卷为例[J].数学教育学报，2019，28（3）：98-102.

    [6]周莹，廖丽红，梁鑫，黄怀芳.初中数学教材与课程标准的一致性研究——以“人教版”和“湘教版”中的函数习题为例[J].数学通报，2017，56（5）：6-9，14.

    [7][8][9]刘学智.论评价与课程标准一致性的构建：美国的经验[J].全球教育展望，2006（9）：35-39.

    [10]刘学智，张雷.学业评价与课程标准的一致性：韦伯模式本土化探究[J].外国教育研究，2009（12）：13-17

    作者简介 吴晓红（1991—），女，广西南宁人，广西师范大学数学与统计学院硕士研究生，主要从事数学课程与教学论研究;

    莫宗赵（1993—），男，广东肇庆人，广西师范大学数学与统计学院硕士研究生，主要从事数学课程与教学论研究;

    周莹（1962—），女，浙江嵊州人，广西师范大学数学与统计学院教授，硕士生导师，主要从事数学课程与教学论研究，本文通讯作者.