粘弹性人工边界在地震工程中应用研究综述
陈宝魁 王东升 成虎
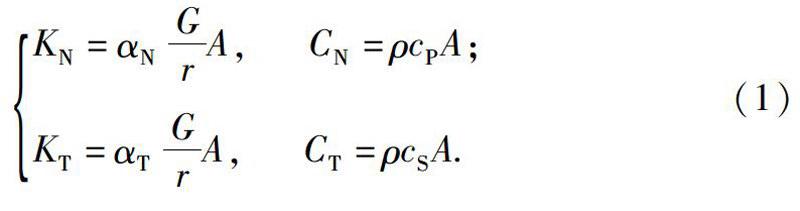

摘要:介绍粘弹性人工边界在结构一地基动力相互作用等问题中应用的研究现状。重点叙述了粘弹性人工边界在有限元计算中的实现方法及其在地震工程中的应用。粘弹性人工边界方法具有方便实现、计算精度高、稳定性强等优点,是解决近场波动问题的一种重要手段。随着粘弹性人工边界理论及其在有限元软件中的应用日渐成熟,其在工程抗震分析等方面将具有广阔的应用前景。
关键词:粘弹性人工边界;地震工程;结构一地基动力相互作用;近场波动
中图分类号:TU432 文献标识码:A 文章编号:1000-0666(2016)01-0137-06
0 引言
诸如大坝、核电站、跨海桥梁等大型工程的抗震分析,一般需要考虑地震波在无限域地基中的传播(辐射阻尼)效应,通常称为结构一地基动力相互作用或近场波动问题(廖振鹏,2002;杜修力,2009;Todorovska,2009;Kausel,2010;Lou et al,2011)。目前有限元方法是解决结构-地基动力相互作用问题的常用手段,如果地基范围截取过大会导致计算量几何级数增大,对于大型工程甚至无法完成运算。从无限域中截取近场有限区域,并在其边界处施加人为处理的虚拟边界条件(Wolf,Song,2002;邱流潮,金峰,2006;Hatzigeorgiou,Beskos,2010;Du,Zhao,2010;Ghandil,Behnamfar,2015)来模拟远场无限地基的辐射阻尼效应,这是当前采用的主要方法。正确定义和设置人工边界,使结构基础或地表产生的散射波在人工边界上被吸收或穿过边界进入无限域,决定了计算是否准确与高效。
基于波动理论提出的人工边界大致可分为时空耦联的全局人工边界和局部人工边界两类。局部人工边界具有实现简单、计算量小等优点,因此被广泛应用(杜修力等,2006),本文讨论的粘弹性人工边界属于局部人工边界中的一种。通常局部人工边界亦可分为位移型人工边界条件(Kausel,1988;Wolf,1986;Higdon,1987,1991;Liao,Wong,1984)与应力型人工边界条件两类。位移人工边界条件用于时步积分时,可能会出现数值失稳,并且此问题尚未得到根本解决;而应力人工边界在有限元积分方法稳定时,不存在人工边界失稳问题(杜修力等,2006)。因此,在近场波动有限元分析中应力型人工边界具有重要的应用价值。应力型人工边界包括粘性边界(Jiao et al,2007)、粘弹性边界(Liu,Lv,1998;刘晶波,吕彦东,1998;刘晶波等,2006a)等。粘弹性人工边界因具有物理意义清晰,精度良好、稳定性好等优点,被众多学者研究并应用于比较各类应力型人工边界在数值分析中的效率与精度。
近年来,研究人员对粘弹性人工边界的理论与应用进行了大量研究(刘晶波等,1998,2006a,b,c,2007;王振宇,刘晶波,2004),并且该方法已经在多种有限元软件中实现,并取得若干研究进展(杜修力,赵密,2006;谷音等,2007;张燎军等,2008;蒋新新等,2013)。由于粘弹性人工边界方法是21世纪初才提出并完善的,大量研究主要集中在近10年。目前在通用的商业有限元软件中尚缺乏相应的独立模块以方便应用,这给设计人员在工程中应用粘弹性人工边界带来了困难,导致粘弹性人工边界在实际工程中的应用与其理论研究进展很不对称。本文综述了粘弹性人工边界方法的研究进展,总结了粘弹性人工边界在多种动力有限元分析软件中的应用成果,并在此基础上提出了粘弹性人工边界在有限元计算与工程应用上的不足与展望。
1 粘弹性人工边界研究进展与实现方法
在早期发展的人工边界理论(廖振鹏,2002;Kausel,1988;Wolf,1986;Higdon,1987,1991)中,相对简单的局部人工边界是Lysmer和Kuhlem-eyer(1969)提出的粘性人工边界,其概念清晰、容易实现,得到了广泛的应用。但粘性人工边界仅考虑对散射波能量的吸收,忽略了半无限地基的弹性恢复能力,因此存在低频稳定性问题,即在低频力作用下可能发生整体漂移。为克服以上问题,Deeks和Randolph(1994)、刘晶波和吕彦东(1998)基于柱面波的波动方程建立了二维粘弹性人工边界。
1.1 粘弹性边界单元实现
考虑介质中辐射阻尼影响的近场波动问题可以采用数值和解析两种计算方法。解析法着重于分析问题本质,计算结果为精确解,但对于大型工程的动力分析,很难用解析的方法解决。相对而言引入粘弹性人工边界的数值法具有很强的适用性和灵活性,方便应用于理论研究与实际工程。
1.1.1 集中粘弹性人工边界
粘弹性人工边界在有限元分析中一般可以等效为在截取的人工边界节点上并联弹簧(K)-阻尼(C)系统,这种处理方法简称为集中粘弹性人工边界。
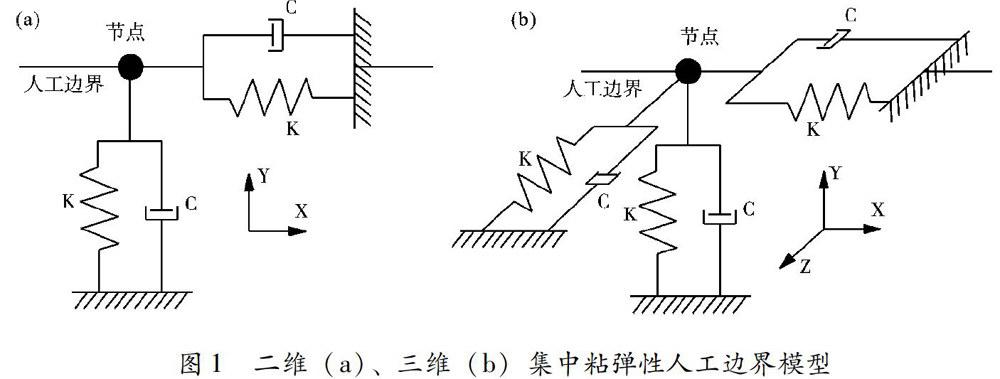
如果将基于全空间波动理论推导的二维粘弹性人工边界应用于半空间问题,粘弹性人工边界的刚度系数将偏大。因此引入人工边界参数αN与αT对粘弹性人工边界中的弹簧刚度系数进行调整。图1为二维与三维粘弹性人工边界模型,其中弹簧与阻尼系统物理参数的公式为(刘晶波等,2005,2006a;Liu et al,2006)式中,KN、KT为法向与切向刚度系数,CN、CT为阻尼器的法向与切向阻尼系数,G为介质剪切模量,cS和cP为S波与P波波速,ρ为密度,r为波源至人工边界的距离,αN、αT为法向与切向粘弹性人工边界的修正系数;在二维问题中,αN的经验取值范围是0.8~1.2,T为0.35~0.65,谷音等(2007)推荐取αN=1.0,αT=0.5;在三维问题中αN的经验取值范围是1.0~2.0,αT取为0.5~1.0,谷音等(2007)、尹广斌等(2012)推荐αN=1.33,αT=0.67;A表示的是单元节点的控制面积。对于直接在边界单元节点施加物理系统的集中粘弹性人工边界,在二维或三维模型中需考虑边界单元节点所控制的边长或面积。王振宇和刘晶波(2004)进一步提出了成层地基中每层介质边界弹簧-阻尼系统的参数;赵密(2004)提出了基于衰减平面散射波的粘弹性人工边界条件。
1.1.2 等效一致粘弹性人工边界
刘晶波等(2006a)在二维集中粘弹性人工边界基础上,提出等效一致粘弹性人工边界及其边界单元的计算方法。假定(分布式)粘弹性人工边界的内部自由度可类似单元一样由差值函数和节点处自由度确定,进而通过与平面固体有限元刚度矩阵对比,可以得到一致粘弹性人工边界单元的相关等效物理参数(刘晶波等,2006a;谷音等,2007):式中,G、E和μ分别为等效一致粘弹性边界单元的等效剪切模量和等效弹性模量和等效泊松比;αN与αT为法向与切向粘弹性人工边界的修正系数,其取值参见式(1);h为边界单元的厚度。如果采用各向同性材料本构关系建立等效一致粘弹性人工边界单元,μ和E并不能独立地按式(2)中的E取值,μ也应同时满足刘晶波等(2006a)推导的式(17)的要求。
刘晶波等(2006a)、谷音等(2007)推导得出另一个重要的单元材料参数,等效粘弹性边界单元的材料阻尼比例系数为
在三维模型中,一致粘弹性人工边界等效单元参数G、E和μ的计算公式与上述提到的二维模型完全相同,但边界单元的材料阻尼比例系数η的求解公式略有不同,为
在二维或三维有限元模型中,比较集中粘弹性人工边界与等效一致粘弹性人工边界的动力分析结果(程恒等,2009),发现两种粘弹性人工边界具有相同的计算精度,且与解析解的结果十分接近;并且两种粘弹性人工边界计算结果的准确性明显好于固定边界与粘性人工边界的计算结果(杜修力等,2006;刘晶波,吕彦东,1998;刘晶波等,2006a,b;谷音等,2007;张燎军等,2008;卢华喜等,2008)。
1.2 粘弹性人工边界的地震动输入方法
粘弹性人工边界有限元模型的波动输入方法主要分为内源问题和外源(波源)问题。内源问题即在人工边界内的模型中考虑波动输入,在人工边界范围内直接输入动力荷载,而产生的散射波可由粘弹性人工边界吸收。内源输入方法相对简单,已在地震工程领域广泛应用(杜修力等,2006;谷音等,2007;刘晶波等,2002,2006a)。
外源问题是指在人工边界外施加波动输入,即在人工边界节点处输入地震动来计算模型的地震响应。Joyner和Chen(1975)最早提出并改进了将波动输入转化为等效荷载输入到粘性人工边界的方法。随后,刘晶波等(1998,2004,2006b)提出了适合粘弹性人工边界的波源输入方法,在边界节点处采用力学中脱离体概念,经推导得到施加于粘弹性人工边界的等效荷载F(t)的公式:
F(t)=τ0(x,y,t)+Ch·ω0(x,y,t)+Kb·ω0(x,y,t). (5)式中,τ0(x,y,t)为人工边界上的节点应力;Ch和K0h分别为粘弹性人工边界的刚度与阻尼系数,可由式(1)确定;ω0(x,y,t)为已知入射位移场,而ω0(x,y,t)与应力τ0(x,y,t)均可由ω0(x,y,t)得到。
2 粘弹性人工边界方法在通用有限元软件中的应用
由于粘弹性人工边界方法在有限元软件中易于实现,因此已经得到相关研究人员的关注,其在SAP、Nastran、ANSYS、LS-DYNA、ADINA、ABAQUS等通用有限元软件中均已实现,且被广泛应用于研究与工程问题。
刘晶波和吕彦东(1998)首先通过编制外挂程序,将粘弹性人工边界分析方法并入Super SAP中。在给定了边界单元参数以及波源输入方法的基础上,分析了二维半圆山谷在平面波入射时的反应,将SAP中的有限元解与解析解对比,发现两种解具有很好的一致性。刘晶波等(2002)同样利用Super SAP对高压聚乙烯装置压缩机基础的动力反应进行分析,结果表明引入粘弹性人工边界对大型动力机器基础进行有限元分析是必要的,并可以给出更合理的基础设计与地基处理方法。
刘晶波等(2006b)结合粘弹性人工边界与振型叠加法对结构一地基相互作用问题进行分析,并将其在有限元软件Nastran中实现,证明了该计算方法准确、高效。另外,刘晶波(2006a)、谷音等(2007)提出等效一致粘弹性人工边界的计算方法,利用Nastran软件将该边界计算方法在二维与三维模型中实现。
刘晶波等(2007)同样将等效一致粘弹性人工边界及其波动输入法在ANSYS软件中实现。徐静等(2009)采用粘弹性人工边界模拟远场无限介质的波动辐射效应,利用ANSYS分析桩-土-输电塔体系相互作用问题。郜新军等(2010,2011)利用多源粘弹性人工边界方法,在ANSYS中实现了考虑斜入射波与局部地形等情况下的结构一地基动力相互作用分析。蒋新新等(2013)通过在ANSYS中构建虚拟对称结构体系,解决了边坡场地条件下粘弹性人工边界模型计算土-结构相互作用分析中,由于外边界输入荷载不一致而导致的结构响应发散或位移漂移问题。宋贞霞和丁海平(2007)研究了粘弹性人工边界在LS-DYNA中的实现。
张燎军等(2008)、尹广斌(2012)、程恒等(2009)实现了粘弹性人工边界在ADINA中的应用,并将结果与粘性边界、固定边界以及扩展边界(精确解)的结果进行比较,验证了粘弹性人工边界计算结构-地基动力相互作用问题的精确性与稳定性。并利用粘弹性人工边界在ADINA中计算了三向地震荷载作用下坝体-地基-库水,以及泵站-地基-水体的动力相互作用算例。张小玲等(2008)采用饱和孔隙介质的Biot动力固结理论,利用粘弹性人工边界在ADINA中建立海床一管线相互作用的计算模型,结果表明粘弹性人工边界在求解瞬态动力问题上比固定边界更优越、更接近于数值解。
梅魁和孟凡深(2010)探讨了粘弹性人工边界在ABAQUS中的实现,并应用其对混凝土重力坝二维横截面模型进行动力分析。陈震和徐远杰(2012)基于波动理论及ABAQUS用户程序实现了粘弹性人工边界单元在ABAQUS中的应用并验证了外源波动输入的准确性。
综上,图2总结了粘弹性人工边界在有限元软件中实现的流程;表1统计了粘弹性人工边界在不同软件中的应用要点与相关成果。
3 结论
粘弹性人工边界的理论在有限元软件中的应用趋于成熟,随着大型工程在抗震分析中对结构一地基动力相互作用的关注日渐增多,其在诸如大坝、核电站、跨海桥梁等重大工程的抗震分析中,将具有广阔的应用前景。
(1)粘弹性人工边界具有物理概念清晰,计算精度高及稳定性强的优点,是考虑地基辐射阻尼及近场波动问题的一种有效计算方法。
(2)粘弹性人工边界目前已在多种通用有限元软件中实现,包括SAP、Nastran、ANSYS、LS-DYNA、ADINA、ABAQUS等。其在诸如大型机器对结构基础动力反应的内源输入问题中,具有方便实现、计算精确等优点,已经在实际工程中广泛应用。
(3)粘弹性人工边界提出的时间相对较短,工程人员对其理论与实现方法尚缺乏足够理解。对于外源输入问题,其在通用有限元软件中一般需要做适当变换或二次开发才能方便应用,这一定程度上影响了粘弹性人工边界在工程问题中的应用。
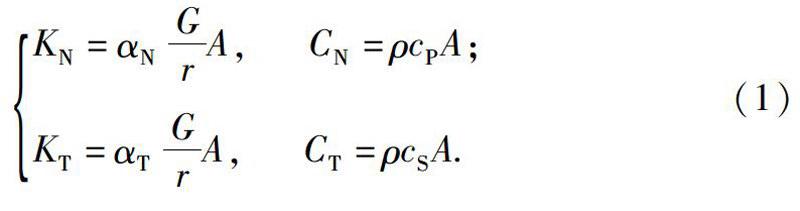


摘要:介绍粘弹性人工边界在结构一地基动力相互作用等问题中应用的研究现状。重点叙述了粘弹性人工边界在有限元计算中的实现方法及其在地震工程中的应用。粘弹性人工边界方法具有方便实现、计算精度高、稳定性强等优点,是解决近场波动问题的一种重要手段。随着粘弹性人工边界理论及其在有限元软件中的应用日渐成熟,其在工程抗震分析等方面将具有广阔的应用前景。
关键词:粘弹性人工边界;地震工程;结构一地基动力相互作用;近场波动
中图分类号:TU432 文献标识码:A 文章编号:1000-0666(2016)01-0137-06
0 引言
诸如大坝、核电站、跨海桥梁等大型工程的抗震分析,一般需要考虑地震波在无限域地基中的传播(辐射阻尼)效应,通常称为结构一地基动力相互作用或近场波动问题(廖振鹏,2002;杜修力,2009;Todorovska,2009;Kausel,2010;Lou et al,2011)。目前有限元方法是解决结构-地基动力相互作用问题的常用手段,如果地基范围截取过大会导致计算量几何级数增大,对于大型工程甚至无法完成运算。从无限域中截取近场有限区域,并在其边界处施加人为处理的虚拟边界条件(Wolf,Song,2002;邱流潮,金峰,2006;Hatzigeorgiou,Beskos,2010;Du,Zhao,2010;Ghandil,Behnamfar,2015)来模拟远场无限地基的辐射阻尼效应,这是当前采用的主要方法。正确定义和设置人工边界,使结构基础或地表产生的散射波在人工边界上被吸收或穿过边界进入无限域,决定了计算是否准确与高效。
基于波动理论提出的人工边界大致可分为时空耦联的全局人工边界和局部人工边界两类。局部人工边界具有实现简单、计算量小等优点,因此被广泛应用(杜修力等,2006),本文讨论的粘弹性人工边界属于局部人工边界中的一种。通常局部人工边界亦可分为位移型人工边界条件(Kausel,1988;Wolf,1986;Higdon,1987,1991;Liao,Wong,1984)与应力型人工边界条件两类。位移人工边界条件用于时步积分时,可能会出现数值失稳,并且此问题尚未得到根本解决;而应力人工边界在有限元积分方法稳定时,不存在人工边界失稳问题(杜修力等,2006)。因此,在近场波动有限元分析中应力型人工边界具有重要的应用价值。应力型人工边界包括粘性边界(Jiao et al,2007)、粘弹性边界(Liu,Lv,1998;刘晶波,吕彦东,1998;刘晶波等,2006a)等。粘弹性人工边界因具有物理意义清晰,精度良好、稳定性好等优点,被众多学者研究并应用于比较各类应力型人工边界在数值分析中的效率与精度。
近年来,研究人员对粘弹性人工边界的理论与应用进行了大量研究(刘晶波等,1998,2006a,b,c,2007;王振宇,刘晶波,2004),并且该方法已经在多种有限元软件中实现,并取得若干研究进展(杜修力,赵密,2006;谷音等,2007;张燎军等,2008;蒋新新等,2013)。由于粘弹性人工边界方法是21世纪初才提出并完善的,大量研究主要集中在近10年。目前在通用的商业有限元软件中尚缺乏相应的独立模块以方便应用,这给设计人员在工程中应用粘弹性人工边界带来了困难,导致粘弹性人工边界在实际工程中的应用与其理论研究进展很不对称。本文综述了粘弹性人工边界方法的研究进展,总结了粘弹性人工边界在多种动力有限元分析软件中的应用成果,并在此基础上提出了粘弹性人工边界在有限元计算与工程应用上的不足与展望。
1 粘弹性人工边界研究进展与实现方法
在早期发展的人工边界理论(廖振鹏,2002;Kausel,1988;Wolf,1986;Higdon,1987,1991)中,相对简单的局部人工边界是Lysmer和Kuhlem-eyer(1969)提出的粘性人工边界,其概念清晰、容易实现,得到了广泛的应用。但粘性人工边界仅考虑对散射波能量的吸收,忽略了半无限地基的弹性恢复能力,因此存在低频稳定性问题,即在低频力作用下可能发生整体漂移。为克服以上问题,Deeks和Randolph(1994)、刘晶波和吕彦东(1998)基于柱面波的波动方程建立了二维粘弹性人工边界。
1.1 粘弹性边界单元实现
考虑介质中辐射阻尼影响的近场波动问题可以采用数值和解析两种计算方法。解析法着重于分析问题本质,计算结果为精确解,但对于大型工程的动力分析,很难用解析的方法解决。相对而言引入粘弹性人工边界的数值法具有很强的适用性和灵活性,方便应用于理论研究与实际工程。
1.1.1 集中粘弹性人工边界
粘弹性人工边界在有限元分析中一般可以等效为在截取的人工边界节点上并联弹簧(K)-阻尼(C)系统,这种处理方法简称为集中粘弹性人工边界。
如果将基于全空间波动理论推导的二维粘弹性人工边界应用于半空间问题,粘弹性人工边界的刚度系数将偏大。因此引入人工边界参数αN与αT对粘弹性人工边界中的弹簧刚度系数进行调整。图1为二维与三维粘弹性人工边界模型,其中弹簧与阻尼系统物理参数的公式为(刘晶波等,2005,2006a;Liu et al,2006)式中,KN、KT为法向与切向刚度系数,CN、CT为阻尼器的法向与切向阻尼系数,G为介质剪切模量,cS和cP为S波与P波波速,ρ为密度,r为波源至人工边界的距离,αN、αT为法向与切向粘弹性人工边界的修正系数;在二维问题中,αN的经验取值范围是0.8~1.2,T为0.35~0.65,谷音等(2007)推荐取αN=1.0,αT=0.5;在三维问题中αN的经验取值范围是1.0~2.0,αT取为0.5~1.0,谷音等(2007)、尹广斌等(2012)推荐αN=1.33,αT=0.67;A表示的是单元节点的控制面积。对于直接在边界单元节点施加物理系统的集中粘弹性人工边界,在二维或三维模型中需考虑边界单元节点所控制的边长或面积。王振宇和刘晶波(2004)进一步提出了成层地基中每层介质边界弹簧-阻尼系统的参数;赵密(2004)提出了基于衰减平面散射波的粘弹性人工边界条件。
1.1.2 等效一致粘弹性人工边界
刘晶波等(2006a)在二维集中粘弹性人工边界基础上,提出等效一致粘弹性人工边界及其边界单元的计算方法。假定(分布式)粘弹性人工边界的内部自由度可类似单元一样由差值函数和节点处自由度确定,进而通过与平面固体有限元刚度矩阵对比,可以得到一致粘弹性人工边界单元的相关等效物理参数(刘晶波等,2006a;谷音等,2007):式中,G、E和μ分别为等效一致粘弹性边界单元的等效剪切模量和等效弹性模量和等效泊松比;αN与αT为法向与切向粘弹性人工边界的修正系数,其取值参见式(1);h为边界单元的厚度。如果采用各向同性材料本构关系建立等效一致粘弹性人工边界单元,μ和E并不能独立地按式(2)中的E取值,μ也应同时满足刘晶波等(2006a)推导的式(17)的要求。
刘晶波等(2006a)、谷音等(2007)推导得出另一个重要的单元材料参数,等效粘弹性边界单元的材料阻尼比例系数为
在三维模型中,一致粘弹性人工边界等效单元参数G、E和μ的计算公式与上述提到的二维模型完全相同,但边界单元的材料阻尼比例系数η的求解公式略有不同,为
在二维或三维有限元模型中,比较集中粘弹性人工边界与等效一致粘弹性人工边界的动力分析结果(程恒等,2009),发现两种粘弹性人工边界具有相同的计算精度,且与解析解的结果十分接近;并且两种粘弹性人工边界计算结果的准确性明显好于固定边界与粘性人工边界的计算结果(杜修力等,2006;刘晶波,吕彦东,1998;刘晶波等,2006a,b;谷音等,2007;张燎军等,2008;卢华喜等,2008)。
1.2 粘弹性人工边界的地震动输入方法
粘弹性人工边界有限元模型的波动输入方法主要分为内源问题和外源(波源)问题。内源问题即在人工边界内的模型中考虑波动输入,在人工边界范围内直接输入动力荷载,而产生的散射波可由粘弹性人工边界吸收。内源输入方法相对简单,已在地震工程领域广泛应用(杜修力等,2006;谷音等,2007;刘晶波等,2002,2006a)。
外源问题是指在人工边界外施加波动输入,即在人工边界节点处输入地震动来计算模型的地震响应。Joyner和Chen(1975)最早提出并改进了将波动输入转化为等效荷载输入到粘性人工边界的方法。随后,刘晶波等(1998,2004,2006b)提出了适合粘弹性人工边界的波源输入方法,在边界节点处采用力学中脱离体概念,经推导得到施加于粘弹性人工边界的等效荷载F(t)的公式:
F(t)=τ0(x,y,t)+Ch·ω0(x,y,t)+Kb·ω0(x,y,t). (5)式中,τ0(x,y,t)为人工边界上的节点应力;Ch和K0h分别为粘弹性人工边界的刚度与阻尼系数,可由式(1)确定;ω0(x,y,t)为已知入射位移场,而ω0(x,y,t)与应力τ0(x,y,t)均可由ω0(x,y,t)得到。
2 粘弹性人工边界方法在通用有限元软件中的应用
由于粘弹性人工边界方法在有限元软件中易于实现,因此已经得到相关研究人员的关注,其在SAP、Nastran、ANSYS、LS-DYNA、ADINA、ABAQUS等通用有限元软件中均已实现,且被广泛应用于研究与工程问题。
刘晶波和吕彦东(1998)首先通过编制外挂程序,将粘弹性人工边界分析方法并入Super SAP中。在给定了边界单元参数以及波源输入方法的基础上,分析了二维半圆山谷在平面波入射时的反应,将SAP中的有限元解与解析解对比,发现两种解具有很好的一致性。刘晶波等(2002)同样利用Super SAP对高压聚乙烯装置压缩机基础的动力反应进行分析,结果表明引入粘弹性人工边界对大型动力机器基础进行有限元分析是必要的,并可以给出更合理的基础设计与地基处理方法。
刘晶波等(2006b)结合粘弹性人工边界与振型叠加法对结构一地基相互作用问题进行分析,并将其在有限元软件Nastran中实现,证明了该计算方法准确、高效。另外,刘晶波(2006a)、谷音等(2007)提出等效一致粘弹性人工边界的计算方法,利用Nastran软件将该边界计算方法在二维与三维模型中实现。
刘晶波等(2007)同样将等效一致粘弹性人工边界及其波动输入法在ANSYS软件中实现。徐静等(2009)采用粘弹性人工边界模拟远场无限介质的波动辐射效应,利用ANSYS分析桩-土-输电塔体系相互作用问题。郜新军等(2010,2011)利用多源粘弹性人工边界方法,在ANSYS中实现了考虑斜入射波与局部地形等情况下的结构一地基动力相互作用分析。蒋新新等(2013)通过在ANSYS中构建虚拟对称结构体系,解决了边坡场地条件下粘弹性人工边界模型计算土-结构相互作用分析中,由于外边界输入荷载不一致而导致的结构响应发散或位移漂移问题。宋贞霞和丁海平(2007)研究了粘弹性人工边界在LS-DYNA中的实现。
张燎军等(2008)、尹广斌(2012)、程恒等(2009)实现了粘弹性人工边界在ADINA中的应用,并将结果与粘性边界、固定边界以及扩展边界(精确解)的结果进行比较,验证了粘弹性人工边界计算结构-地基动力相互作用问题的精确性与稳定性。并利用粘弹性人工边界在ADINA中计算了三向地震荷载作用下坝体-地基-库水,以及泵站-地基-水体的动力相互作用算例。张小玲等(2008)采用饱和孔隙介质的Biot动力固结理论,利用粘弹性人工边界在ADINA中建立海床一管线相互作用的计算模型,结果表明粘弹性人工边界在求解瞬态动力问题上比固定边界更优越、更接近于数值解。
梅魁和孟凡深(2010)探讨了粘弹性人工边界在ABAQUS中的实现,并应用其对混凝土重力坝二维横截面模型进行动力分析。陈震和徐远杰(2012)基于波动理论及ABAQUS用户程序实现了粘弹性人工边界单元在ABAQUS中的应用并验证了外源波动输入的准确性。
综上,图2总结了粘弹性人工边界在有限元软件中实现的流程;表1统计了粘弹性人工边界在不同软件中的应用要点与相关成果。
3 结论
粘弹性人工边界的理论在有限元软件中的应用趋于成熟,随着大型工程在抗震分析中对结构一地基动力相互作用的关注日渐增多,其在诸如大坝、核电站、跨海桥梁等重大工程的抗震分析中,将具有广阔的应用前景。
(1)粘弹性人工边界具有物理概念清晰,计算精度高及稳定性强的优点,是考虑地基辐射阻尼及近场波动问题的一种有效计算方法。
(2)粘弹性人工边界目前已在多种通用有限元软件中实现,包括SAP、Nastran、ANSYS、LS-DYNA、ADINA、ABAQUS等。其在诸如大型机器对结构基础动力反应的内源输入问题中,具有方便实现、计算精确等优点,已经在实际工程中广泛应用。
(3)粘弹性人工边界提出的时间相对较短,工程人员对其理论与实现方法尚缺乏足够理解。对于外源输入问题,其在通用有限元软件中一般需要做适当变换或二次开发才能方便应用,这一定程度上影响了粘弹性人工边界在工程问题中的应用。

