基于神经网络的光栅莫尔条纹误差模型参数优化

    杨仁付+金佑来+金仁贵

    

    

    

    摘要：光栅莫尔条纹的误差模型是一种多峰的复杂正弦波动函数级数形式，单一的基于导数的非线性参数拟合方法可能无效，神经网络方法不依赖于函数导数，仿真实验表明模型参数的拟合符合实际。

    关键词：神经网络；光栅莫尔条纹；参数拟合

    中图分类号：TP18 文献标识码：A 文章编号：1009-3044（2016）12-0204-02

    Abstract： The error model of grating moire fringe is a multi peak complex sine wave function in series form， simply based on the derivative of the nonlinear parameter fitting method may be invalid. Neural network method does not rely on the derivative of the function， the simulation experiments show that the fitting of model parameters are consistent with the actual.

    Key words： neural network； grating moire fringe； parameter fitting

    1 概述

    光栅长周期不匀误差会导致莫尔条纹波形的正交性和正弦性变差，给信号检测和处理带来系统误差[1]，甚至导致无法读取信号波形，通过对莫尔条纹误差进行分析，建立误差理论模型，对误差的产生、控制有重要意义。

    模型函数的参数拟合，本质上对含有参数的某种误差函数的优化。尽管有各种形式的优化方法，有基于函数导数的各种牛顿与拟牛顿方法、共轭梯度法、非线性最小二乘法，以及不需要函数导数的各种直接方法和智能算法，但都不能直接用于本项目所涉及的模型函数，它是一个复杂的具有级数形式的正弦波动函数

    2神经网络算法

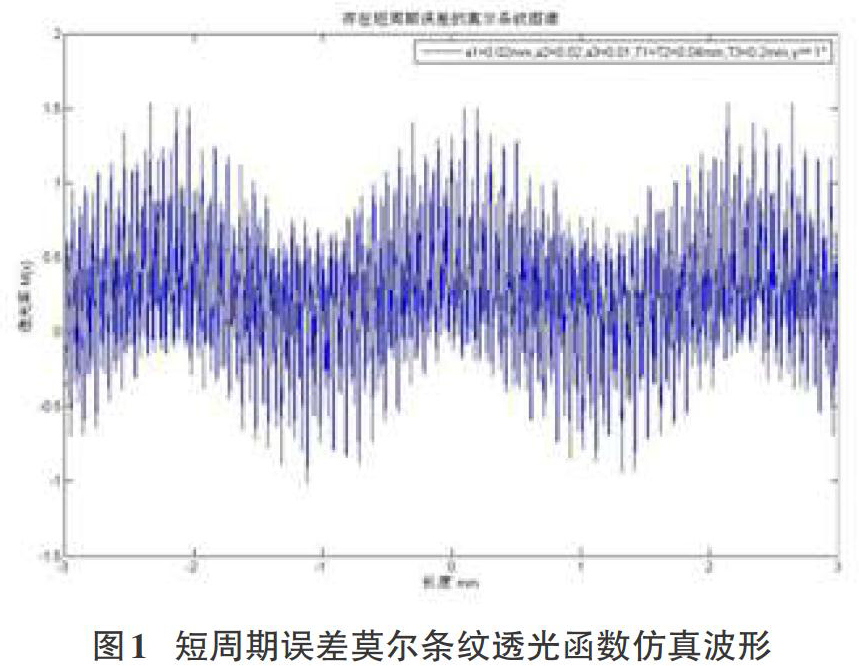
    如图1所示的BP网络是三层结构，包括输入层、隐含层和输出层，采用输出反馈算法。

    但是，BP网络有以下一些主要缺陷[3，]：

    1）存在局部极值问题，且收敛速度慢

    2）网络的输入、输出单元数和隐含层难以确定，要根据经验，无理论指导规则；

    3）存在过学习现象，网络泛化能力较差

    4 结束语

    本文研究的目标函数模型是通过理论研究得出的，难点在于它是隐函数，又带有级数形式，其误差形式是多峰多谷，相当繁杂，用现有的基于导数的优化方法进行参数拟合难以奏效，而神经网络方法不依赖于函数导数，鲁棒性强，但也存在过学习和局部极小点现象，学习过程较为复杂。

    参考文献：

    [1] 朱孝立，陈军宁.基于Ronchi光栅的莫尔条纹函数建模[J].系统仿真学报，2010，22（1）：12-15.

    [2] 杨仁付，朱孝立，陈军宁.Ronchi光栅误差的数值仿真[J].激光技术，2012，1（36）：37-39.

    [3] 杨仁付.基于遗传算法的BP神经网络在建模预测中的应用[J].铜陵学院学报，2007，5（6）：72-74.

    [4] 徐俊波.反馈神经网络进展[J].化工自动化及仪表，2003，30（1）：6-10.

    [5] 阎平凡，张长水.人工神经网络与模拟进化计算[M].北京：清华大学出版社，2000.

    [6] 许东，吴铮.基于MATLAB6.x的系统分析与设计[M].西安：西安电子科技大学出版社，2002.

    [7] 梁志国，张大治，孙王景宇，等.四参数正弦曲线拟合的快速算法[J].计测技术，2006，26（1）：4-7.

    [8] 金佑来.混合误差回归参数估计的强相合性的一个注记[J].广西民族师范学院学报，2012（3）：1-4.

    [9] 金佑来.混合误差线性模型回归参数估计的强相合性[J].池州学院学报，2011（6）：26-27.