基于混沌和FRFT的彩色图像加密算法

    邢丽坤+华正春+牛秀龄+李昕+武月

    

    

    

    摘要：为了增强图像的保密性，恢复原彩色图像信息，提出了一种基于混沌和分数阶Fourier变换的彩色图像信息加密的算法。具体加密过程为：首先将原图像信号分为[R、G、B]三个灰色图像，其次对各个图像做混沌算法加密，最后再进行离散FRFT加密，输出最终的密文。利用MATLAB的仿真实验表明，此算法的图像加密和解密效果较好，能够较好的隐藏和保存彩色图像的信息。

    关键词：混沌加密；FRFT；彩色图像加密

    中图分类号：TP18 文献标识码：A 文章编号：1009-3044（2016）12-0201-03

    Abstract： In order to strengthen the confidentiality of the image， and to restore the original color image information. This paper proposes a color image based on chaos and fractional Fourier transform encryption algorithm. Specific process is： First of all， Let the image is divided into three parts，for R、G、B. And then the chaotic encryption， finally the discrete FRFT encryption. Use of MATLAB simulation show that the algorithm has good encryption and decryption，It can better hide and save the information of color image.

    Key words： chaotic encryption； FRFT； color image encryption

    随着互联网和计算机的迅速发展，作为信息载体的图像的安全性保障也受到越来越多人的关注。但是因某些图像所包含的信息是涉及个人隐私且不便为外人所知的，甚至有些是牵涉国家安全机密的，故图像信息的保密性也变得越来越重要[1]。

    在以往分数阶Fourier变换的加密算法中，虽然因阶次敏感而加密算法较多，但是其对分数阶域的少量系数进行加密，加密的隐蔽性稍差，且使用的是单色光照输入图像，使解密图像丢失了原有的色彩[2]。为加强加密效果，恢复原有的彩色图像，本文将混沌变换和FRFT相结合，以此来更好的加密和恢复彩色图像的信息。

    1 混沌和FRFT的基本理论

    1.1 分数阶Fourier变换的理论

    在对图像信号进行加密处理时，要利用离散的傅里叶变换做算法运行，且利用二位FRFT的可叠加性，可分为两次一维离散FRFT加密，分别有两个变换阶次，两个随机纯相位掩膜，故而可以进一步增强图像加密算法的隐秘性和可靠性[4]。

    1.2 混沌加密

    混沌系统加密应用的序列是由系统迭代产生的，混沌系统具有随机性以及敏感性等等[5]。且使用混沌加密的另一优点就是：由混沌序列的方程是很难猜到其初始值的。在使用其加密时先应用混沌系统对图像的行和列置乱加密，有混沌序列控制每一行循环的位数，同样也要对每一列循环若干次[6]。

    但是仅仅使用混沌加密图像信息，也有些不足之处：计算精度的限制以及周期性的混沌序列使得安全性有时较低，在低位的混沌系统加密中隐秘和保密性不够高[7]。针对单一的混沌加密的不足，此文提出将混沌系统和FRFT结合起来，以此提高图像信息的隐秘性，以及更好地恢复彩色图像的信息[8]。

    1.3 彩色图像加密和解密过程

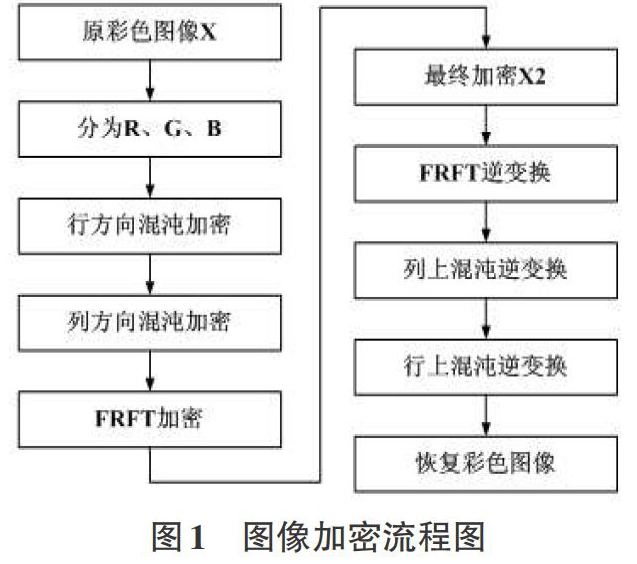
    本文的混沌和FRFT加密相结合的彩色图像加密算法的大致过程如下：

    1）先读取彩色图像，将其分为[R、G]、[B]三部分灰度图像[9]，如图2；

    2）利用混沌系统加密对R、G、B三部分分别在行和列方向上加密，得到混沌加密图像R1、G1、B1，如图3；

    3）对R1、G1、B1做两次一维的FRFT，其中相位掩膜和阶次都是随机可变的[10，11]，得到最终的加密图像R2、G2、B2，如图4；

    4）解密是编码的逆变换，先对最终的加密图像R2、G2、B2做FRFT的逆变换，然后在对其在列和行上做混沌加密的逆变换，如图5、6，

    5）把R2、G2、B2的灰度图像结合在一起恢复成原彩色图像，如图7。

    下图此算法的流程图如下：

    2 仿真和分析

    2.1 仿真结果

    2.2 仿真分析

    通过MATLAB的仿真可知，图2是原始彩色图像分解成三部分灰度图像，各代表图像的红色、绿色和蓝色分量；图3是经过混沌系统加密的图像，图4是在经过离散FRFT加密的图像，比较看出两者结合的加密更能隐藏原图像信息，图6、图7是解密后的图像，和原彩色图像1比较，原图像信息和颜色都可以完整的显示出来。图8是混沌解密密钥错误时的图像，图9是FRFT解密密钥不对时的图像，比较图6、7、8、9可看出任意混沌密钥和分数阶的密钥不正确时，得出的图像都不能正确的显现出三种分量的图像以及原图像的信息。

    从表1可以看出，即使阶次的误差很小，均方误差的值也是很大的，[psnr]得值也较小，使得彩色图像恢复的失真；只有在正确的密钥时，MSE的值最小和[psnr]值最大，图像才能准确的呈现。

    3 结论

    本文提出了一种基于混沌系统加密和离散FRFT加密的算法，实现了此算法对图形的多次加密解密过程，使得两种算法得到互补，提高了信息的隐蔽性以及较好地恢复了彩色图形的信息。通过MATLAB的仿真实验表明，此方法可以较好地对图像信息保密，且较准确的恢复彩色图像的信息。通过表1可知此算法对密钥的误差比较敏感，使阶次的误差很小，均方误差的值也是很大的，[psnr]得值也会变小，即在正确密钥的情况下，MSE的值最小和[psnr]值最大，图像信息才能较好地恢复，也由此加强了图像信息的安全特性。

    参考文献：

    [1] 崔得龙，肖明，左敬龙. 一种基于分数阶傅里叶变换的改进图像加密算法[J].成都信息工程学院学报，2010，25（1）：22-25.

    [2] 王静. 分数阶傅里叶变换在信号处理和图像滤波中的研究[D].上海： 华东师范大学，2007：36-43.

    [3] 陶然， 邓兵， 王越. 分数阶傅里叶变换及其应用[M].北京： 清华大学出版社，2009：12-132.

    [4] H. M. Ozaktas and B. Barshan. D Mendlovic and LOnural. Convolution， Filtering， and Multiplexing in fractional Fourier Domains and their relation to Chirp and Wavelet Transforms [J]. J. Opt. Soc . Amer. A. ，1994，11（2）：547-559.

    [5] 张文全，薛侠，周南润.基于相位恢复和混沌图的多图像并行加密算法[J].计算机工程与应用，2012.48（23）.63-66.

    [6] V.Namias. The fraction order Fourier transform and its application to quantum mechanics [J]. J of Appl Math ，1980（25）：241-265.

    [7] 王银花，柴晓冬，周成鹏，等. 基于分数阶傅里叶变换的混沌图像加密方法[J].计算机工程，2007，33（12）：172-174.

    [8] 杨倬，冯久超，方霞. 一种基于混沌和分数级傅里叶的图像加密算法[J].计算机科学，2008，35（9）：239-240.

    [9] 何俊发，李俊，王红霞. 不对称离散分数阶傅里叶变换实现数字图像的加密变换[J].光学技术，2005，31（ 3） ：410-412.

    [10] V. A shok Narayanan：， K.M.M. Prabhu. The Fractional Fourier transform： Theory， Implementation and Eorr Analysis[J]. Microprocessors and Microsystems，2003（27）：5111-521.

    [11] 王雅庆，周尚波. 基于分数阶Fourier变换的数字图像加密算法研究[J].计算机应用研究，2011，28（7）： 2738-2741.

    [12] 张兆祥，田沛.基于分数阶傅立叶变换的图像加密研究[J].仪器仪表用户，2007，14（5）：87-88.