结构物理参数时域识别的振动台试验研究
王祥建 崔杰


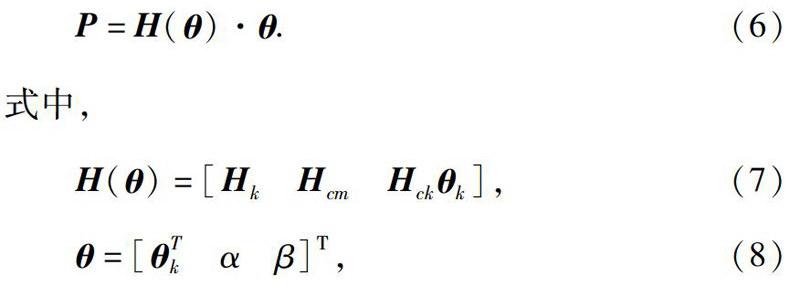
摘要:在输入未知条件下,为了识别非线性参数系统,并消除噪声异常点的影响,引入修正Levenberg-Mar-quardt法和矩形窗法,建立SVD-mLM法,改进了复合反演算法。为了验证改进算法,设计一个五层单跨钢框架模型进行振动台试验,测试获得含有真实噪声的动力响应,采用改进的复合反演算法,研究了结构物理参数时域识别和输入反演问题。振动台试验研究表明结构物理参数识别和输入反演结果是可信的,验证了SVD-mLM法、矩形窗法和改进的复合反演算法在识别结构物理参数和反演输入时的可行性和有效性。
关键词:振动台试验;结构物理参数识别;地震动反演;复合反演算法;非线性参数系统
中图分类号:TU352 文献标识码:A 文章编号:1000-0666(2016)01-0114-06
0 引言
复杂系统的动力特性往往需要通过系统识别确定出来,以便满足某些需求。结构动力学中的系统识别方法,通常是用来求解逆问题,利用已测量的数据识别结构的动力特性。随着计算技术、试验技术和有效数学工具的高速发展,系统识别已成为土木工程领域内的重要研究方向,这是因为系统识别技术能够调查并减小土木结构与其设计模型的差异,对于数值分析中建立完善有限元模型和振动台试验中优化设计试验模型,都有着至关重要的现实意义。在结构健康检测中的损伤识别方面,系统识别也扮演着同样重要的角色,可以通过系统识别方法获得动荷载(如地震、爆炸等)作用后结构的动力特性,了解结构系统的当前状况,并开展相应的处理措施。
对于土木工程的动力学系统,在通常情况下数学模型是已知的,系统识别的过程仅需要获得结构参数,故可称为参数识别。在过去的四十多年里,国内外许多学者开展了大量的参数识别研究,并提出了许多行之有效的研究方法。如:人工神经网络法(Artificial Neural Network Approach,简称ANN)(Huang et al,2003)、小波分析法(Wavelet Analysis Method,简称WAM)(Shi,Chang,2012)、基于傅里叶变换的方法(FourierTransform Based Method,简称FTM)(Rocco et al,2012)、基于有限元迭代最小二乘法(Finite Ele-ment-based Iterative Least-squares Methods,简称ILS)(Wang,Haldar,1994;王祥建等,2008,2015;Wang,Cui,2011)、多模型自适应遗忘与外生变量自回归耦合法(Adaptive Forgettingthrough Multiple Models and auto-regression with Ex-ogenous Variables,简称AFMM-ARX)(Gong et al,2014)、频域分解法(Frequency Domain Decomposi-tion,简称FDD)(Brincker et al,2001)、自然激励技术与特征系统实现算法联合法(Natural Excita-tion Technique and Eigen-system Realization Mlgo-rithm,简称NExT-ERA)(Siringoringo,Fujino,2008)、随机减量技术(Random Decrement Tech-nique,简称RDT)(Ibrahim,1977)、扩展卡尔曼滤波技术(Extended Kalman Filter Technique,简称EKF)(Toki et al,1989;尚久铨,1991)等。
一般来说,利用动力测试数据识别结构参数时,时域法能够避免频域法中时频变换引起的截断误差,从而提高参数识别的精度。用结构物理参数评估结构状态,比模态参数更直观明了。采用单元水平的有限元迭代最小二乘法,能够识别出每个单元(每个构件或者再细分的每段构件)的结构参数,这样即可非常准确的定位损伤。在实际工程动力测试中,因各种制约条件的存在,输入信息往往很难被准确获得(王祥建,201 1)。针对这些原因,王祥建等(2011,2015)基于复合反演方法、引入矩形窗法建立SVD-mLM(sin-gular value decomposition coupled with modified Lev-enberg-Marquardt)方法求解非线性参数方程,数值结果表明改进的复合反演法在噪声存在的条件下,能够较高精度地识别结构参数或损伤。本文将通过对五层结构模型的振动台试验,进一步验证该改进的复合反演法的鲁棒性和有效性。
1 方法
1.1 复合反演法
针对线性参数系统(参数识别方程为线性),基于经典最小二乘法可获得结构参数的估计值
1.2 矩形窗法
在工程结构的动力测试时,每个测试数据常含有测量噪声,且噪声污染程度各不相同,其中受噪声污染严重的测试点称为异常点,利用含有异常点的一段测试信息识别参数和反演输入,计算结果势必存在较大的误差。
若已获得L个连续采样数据,采用固定长度为S(S≤L)的矩形窗选取采样数据,设定参数初值,利用复合反演法进行第一次参数识别和输入反演;然后,以上一次参数识别值为参数初值,将矩形窗向前移动一个数据(即增加1个新数据,剔除最前端1个旧数据),再次进行复合反演运算;持续计算,直至矩形窗无新数据或者达到矩形窗设定个数,共进行了M(M≤L-S+1)次复合反演计算,获得M组参数估计值和M段输入反演时程,该方法称之为矩形窗法。对应同名参数或同时刻输入,再利用统计平均法,即可获得最终的参数识别值和对应的输入反演时程,这样即可减弱数据异常点引起的较大误差。为了提高精度,还可剔除参数识别异常值对应的复合反演结果。
1.3 SVD-mLM法
对于Rayleigh比例阻尼的n自由度剪切型结构而言,参数识别方程为非线性方程:其中,θ为待识别参数向量;θk为刚度参数向量,α和β为比例阻尼系数;ki为θk的第i个刚度分量。
利用修正的Levenberg-Marquardt(简称mLM)法求解非线性参数识别方程(6)(非线性最小二乘问题),可取
显然,mLM法需要给定参数初值,因结构刚度和阻尼参数的量级相差特别大,该法对参数初值非常敏感。为解决这一问题,联合不需参数初值的线性SVD法,即:首先利用SVD法确定参数的近似估计值,以此作为参数初值,再利用mLM法求解非线性参数识别方程,简称SVD-mLM法。
2 试验
2.1 试验概况
本文设计了一个5层单跨钢框架结构试验模型(模型立面图和平面图如图1所示;实际模型及传感器布置如图2所示),进行振动台试验(振动台振动方向为图1a立面图平面内左右方向,也即图1b平面图平面内上下方向;柱子尺寸为图1b中楼板两侧的4根横截面8mm×80mm钢板柱),以测试剪切型结构在地面运动作用下的动力响应,验证结构物理参数时域识别的改进的复合反演算法。
试验采用的传感器型号(制造单位或品牌):位移计为SW-1型相对位移传感器(中国地震局工程力学研究所);速度计为941B型拾振器(中国地震局工程力学研究所);加速度计为LC0405T型压电传感器(朗斯);放大器为CA-3积分电荷放大器(北戴河电子仪器厂);数据采集系统为太平洋6000数采系统(太平洋设备公司);采集软件为P1660(太平洋设备公司)。
采用集中质量法,试验模型各层的质量为:m1=102.5856kg,m2=101.9866kg,m3=m4=101.3875kg,m5=98.8915kg。假定阻尼为Ray-leigh比例阻尼,在振动台试验之前先进行模态试验,采用初位移法(顶层钢板施加)和初速度法(第3、4层钢板之间施加)分别确定模型结构沿该方向第一、第二阶振型,并确定相应频率和阻尼比。由模态分析的结果计算出Rayleigh阻尼系数为:α=0.439193075;β=0.00035487。
本文分别以峰值为0.48g的EL Centro地震波和峰值为0.1g、频率为5Hz的余弦波为激励输入进行振动台试验,测试获得结构模型各层的加速度响应时程(速度及位移响应测试仅用于试验数据重构信息的比较),然后假定输入信息未知,采用改进的复合反演算法进行结构物理参数的时域识别和基底输入的反演研究。
2.2 余弦波(0.1g,5Hz)
图3和图4分别为余弦波激励时振动台面实测加速度时程曲线和各层相对加速度时程曲线(仅以第1、3、5层示例)。利用基于矩形窗法、SVD-mLM法改进的复合反演算法识别非线性参数系统,参数初值为1.0。结构模型物理参数识别结果列入表1,地震动反演结果如图5所示。
2.3 EL Centro地震波(0.48g)
图6和图7分别为EL Centro波激励时振动台面实测加速度时程曲线和各层相对加速度时程曲线(仅以第1、3、5层示例)。利用基于矩形窗法、SVD-mLM法改进的复合反演算法识别非线性参数系统,参数初值为1.0。结构模型物理参数识别结果列入表2,地震动反演结果如图8所示。
从表1可知,振动台激励为峰值0.1g振幅稳定变化的余弦波时,识别得到的Rayleigh阻尼系数α和β与模态试验的分析结果相比较,误差分别为10.82%和45.10%,说明结构实际的阻尼是非常复杂的。从图5可知,反演的输入时程和振动台台面实测时程是完全吻合的,这也能说明结构模型物理参数识别结果是可信的。
从表2可知,振动台激励为峰值0.48g振幅急剧变化的EL Centro地震波时,基于10~16s时间段的测试数据识别得到的阻尼系数出现负值,说明真实阻尼并不完全符合Rayleigh比例阻尼假定;随矩形窗的前移,参数识别值有所变化(阻尼系数变化较大),表明在真实的震动作用下结构模型实际状态非常复杂。从图8可知,反演的地震动时程与振动台台面实测时程存在较大误差,但前者能够很好地追踪到后者的变化和峰值,这也说明识别出的参数平均值能够反映结构模型在10~16s地震动作用下所处的复杂状态。
结构模型在两种不同输入激励下,识别的结构物理参数有较大差异,分析其可能原因为:输入为小振幅平稳变化的余弦波时,结构模型侧移幅度较小,每层钢板重量基本垂直施压在立柱上并向下传递,大质量钢板在一定程度上约束了立柱,增大了刚度、减小了侧移,试验模型更接近于理想的剪切型结构。输入为大振幅急剧变化的地震波时,结构模型侧移幅度较大且剧烈摇摆,较柔的立柱弯曲角度较大,致使钢板与立柱连接的角钢螺栓发生松动,板柱连接不再是刚性连接,层间有效高度增大、刚度减小,侧移增大,在螺栓松动的情况下,钢板和立柱也会发生碰撞,使试验模型在地震动激励下处于复杂状态。
基于振动台试验测试数据,利用修正的复合反演算法,识别结构物理参数和反演输入,产生误差的原因有:(1)材料误差(实际值与设计值不符);(2)设计误差(节点的角钢螺栓连接影响有效高度等);(3)制作误差(尺寸不准、螺栓不紧等);(4)试验误差(振动台、仪器等产生的误差);(5)计算误差(试验模型理想化、测试噪声、数值模型简化等问题)等。
3 结论
在输入未知条件下,为了识别非线性参数系统,并消除噪声异常点的影响,引入修正Leven-berg-Marquardt法和矩形窗法,建立SVD-mLM法,改进了复合反演算法,数值研究已经验证了改进的复合反演算法的有效性和鲁棒性。本文设计了一个5层单跨钢框架模型,采用改进的复合反演算法,开展了噪声真实存在情形下结构物理参数时域识别和输入反演的振动台试验研究,结果验证了矩形窗法、SVD-mLM法和改进的复合反演算法在识别结构物理参数和反演输入时的可行性和有效性。
对本文的振动台试验结果进行分析,认为试验模型的板柱连接节点需要进一步改进设计,使之更接近于刚性节点,从而使试验模型更近似于理想化的数值模型。


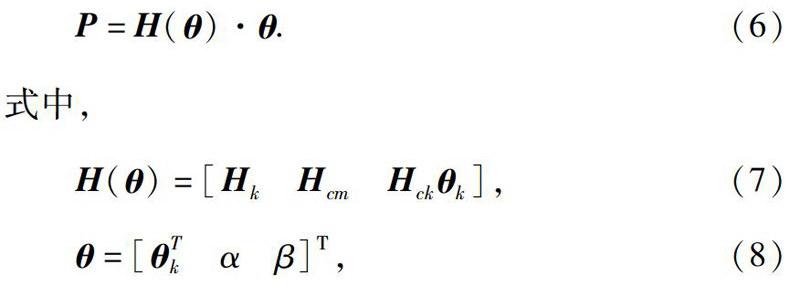
摘要:在输入未知条件下,为了识别非线性参数系统,并消除噪声异常点的影响,引入修正Levenberg-Mar-quardt法和矩形窗法,建立SVD-mLM法,改进了复合反演算法。为了验证改进算法,设计一个五层单跨钢框架模型进行振动台试验,测试获得含有真实噪声的动力响应,采用改进的复合反演算法,研究了结构物理参数时域识别和输入反演问题。振动台试验研究表明结构物理参数识别和输入反演结果是可信的,验证了SVD-mLM法、矩形窗法和改进的复合反演算法在识别结构物理参数和反演输入时的可行性和有效性。
关键词:振动台试验;结构物理参数识别;地震动反演;复合反演算法;非线性参数系统
中图分类号:TU352 文献标识码:A 文章编号:1000-0666(2016)01-0114-06
0 引言
复杂系统的动力特性往往需要通过系统识别确定出来,以便满足某些需求。结构动力学中的系统识别方法,通常是用来求解逆问题,利用已测量的数据识别结构的动力特性。随着计算技术、试验技术和有效数学工具的高速发展,系统识别已成为土木工程领域内的重要研究方向,这是因为系统识别技术能够调查并减小土木结构与其设计模型的差异,对于数值分析中建立完善有限元模型和振动台试验中优化设计试验模型,都有着至关重要的现实意义。在结构健康检测中的损伤识别方面,系统识别也扮演着同样重要的角色,可以通过系统识别方法获得动荷载(如地震、爆炸等)作用后结构的动力特性,了解结构系统的当前状况,并开展相应的处理措施。
对于土木工程的动力学系统,在通常情况下数学模型是已知的,系统识别的过程仅需要获得结构参数,故可称为参数识别。在过去的四十多年里,国内外许多学者开展了大量的参数识别研究,并提出了许多行之有效的研究方法。如:人工神经网络法(Artificial Neural Network Approach,简称ANN)(Huang et al,2003)、小波分析法(Wavelet Analysis Method,简称WAM)(Shi,Chang,2012)、基于傅里叶变换的方法(FourierTransform Based Method,简称FTM)(Rocco et al,2012)、基于有限元迭代最小二乘法(Finite Ele-ment-based Iterative Least-squares Methods,简称ILS)(Wang,Haldar,1994;王祥建等,2008,2015;Wang,Cui,2011)、多模型自适应遗忘与外生变量自回归耦合法(Adaptive Forgettingthrough Multiple Models and auto-regression with Ex-ogenous Variables,简称AFMM-ARX)(Gong et al,2014)、频域分解法(Frequency Domain Decomposi-tion,简称FDD)(Brincker et al,2001)、自然激励技术与特征系统实现算法联合法(Natural Excita-tion Technique and Eigen-system Realization Mlgo-rithm,简称NExT-ERA)(Siringoringo,Fujino,2008)、随机减量技术(Random Decrement Tech-nique,简称RDT)(Ibrahim,1977)、扩展卡尔曼滤波技术(Extended Kalman Filter Technique,简称EKF)(Toki et al,1989;尚久铨,1991)等。
一般来说,利用动力测试数据识别结构参数时,时域法能够避免频域法中时频变换引起的截断误差,从而提高参数识别的精度。用结构物理参数评估结构状态,比模态参数更直观明了。采用单元水平的有限元迭代最小二乘法,能够识别出每个单元(每个构件或者再细分的每段构件)的结构参数,这样即可非常准确的定位损伤。在实际工程动力测试中,因各种制约条件的存在,输入信息往往很难被准确获得(王祥建,201 1)。针对这些原因,王祥建等(2011,2015)基于复合反演方法、引入矩形窗法建立SVD-mLM(sin-gular value decomposition coupled with modified Lev-enberg-Marquardt)方法求解非线性参数方程,数值结果表明改进的复合反演法在噪声存在的条件下,能够较高精度地识别结构参数或损伤。本文将通过对五层结构模型的振动台试验,进一步验证该改进的复合反演法的鲁棒性和有效性。
1 方法
1.1 复合反演法
针对线性参数系统(参数识别方程为线性),基于经典最小二乘法可获得结构参数的估计值
1.2 矩形窗法
在工程结构的动力测试时,每个测试数据常含有测量噪声,且噪声污染程度各不相同,其中受噪声污染严重的测试点称为异常点,利用含有异常点的一段测试信息识别参数和反演输入,计算结果势必存在较大的误差。
若已获得L个连续采样数据,采用固定长度为S(S≤L)的矩形窗选取采样数据,设定参数初值,利用复合反演法进行第一次参数识别和输入反演;然后,以上一次参数识别值为参数初值,将矩形窗向前移动一个数据(即增加1个新数据,剔除最前端1个旧数据),再次进行复合反演运算;持续计算,直至矩形窗无新数据或者达到矩形窗设定个数,共进行了M(M≤L-S+1)次复合反演计算,获得M组参数估计值和M段输入反演时程,该方法称之为矩形窗法。对应同名参数或同时刻输入,再利用统计平均法,即可获得最终的参数识别值和对应的输入反演时程,这样即可减弱数据异常点引起的较大误差。为了提高精度,还可剔除参数识别异常值对应的复合反演结果。
1.3 SVD-mLM法
对于Rayleigh比例阻尼的n自由度剪切型结构而言,参数识别方程为非线性方程:其中,θ为待识别参数向量;θk为刚度参数向量,α和β为比例阻尼系数;ki为θk的第i个刚度分量。
利用修正的Levenberg-Marquardt(简称mLM)法求解非线性参数识别方程(6)(非线性最小二乘问题),可取
显然,mLM法需要给定参数初值,因结构刚度和阻尼参数的量级相差特别大,该法对参数初值非常敏感。为解决这一问题,联合不需参数初值的线性SVD法,即:首先利用SVD法确定参数的近似估计值,以此作为参数初值,再利用mLM法求解非线性参数识别方程,简称SVD-mLM法。
2 试验
2.1 试验概况
本文设计了一个5层单跨钢框架结构试验模型(模型立面图和平面图如图1所示;实际模型及传感器布置如图2所示),进行振动台试验(振动台振动方向为图1a立面图平面内左右方向,也即图1b平面图平面内上下方向;柱子尺寸为图1b中楼板两侧的4根横截面8mm×80mm钢板柱),以测试剪切型结构在地面运动作用下的动力响应,验证结构物理参数时域识别的改进的复合反演算法。
试验采用的传感器型号(制造单位或品牌):位移计为SW-1型相对位移传感器(中国地震局工程力学研究所);速度计为941B型拾振器(中国地震局工程力学研究所);加速度计为LC0405T型压电传感器(朗斯);放大器为CA-3积分电荷放大器(北戴河电子仪器厂);数据采集系统为太平洋6000数采系统(太平洋设备公司);采集软件为P1660(太平洋设备公司)。
采用集中质量法,试验模型各层的质量为:m1=102.5856kg,m2=101.9866kg,m3=m4=101.3875kg,m5=98.8915kg。假定阻尼为Ray-leigh比例阻尼,在振动台试验之前先进行模态试验,采用初位移法(顶层钢板施加)和初速度法(第3、4层钢板之间施加)分别确定模型结构沿该方向第一、第二阶振型,并确定相应频率和阻尼比。由模态分析的结果计算出Rayleigh阻尼系数为:α=0.439193075;β=0.00035487。
本文分别以峰值为0.48g的EL Centro地震波和峰值为0.1g、频率为5Hz的余弦波为激励输入进行振动台试验,测试获得结构模型各层的加速度响应时程(速度及位移响应测试仅用于试验数据重构信息的比较),然后假定输入信息未知,采用改进的复合反演算法进行结构物理参数的时域识别和基底输入的反演研究。
2.2 余弦波(0.1g,5Hz)
图3和图4分别为余弦波激励时振动台面实测加速度时程曲线和各层相对加速度时程曲线(仅以第1、3、5层示例)。利用基于矩形窗法、SVD-mLM法改进的复合反演算法识别非线性参数系统,参数初值为1.0。结构模型物理参数识别结果列入表1,地震动反演结果如图5所示。
2.3 EL Centro地震波(0.48g)
图6和图7分别为EL Centro波激励时振动台面实测加速度时程曲线和各层相对加速度时程曲线(仅以第1、3、5层示例)。利用基于矩形窗法、SVD-mLM法改进的复合反演算法识别非线性参数系统,参数初值为1.0。结构模型物理参数识别结果列入表2,地震动反演结果如图8所示。
从表1可知,振动台激励为峰值0.1g振幅稳定变化的余弦波时,识别得到的Rayleigh阻尼系数α和β与模态试验的分析结果相比较,误差分别为10.82%和45.10%,说明结构实际的阻尼是非常复杂的。从图5可知,反演的输入时程和振动台台面实测时程是完全吻合的,这也能说明结构模型物理参数识别结果是可信的。
从表2可知,振动台激励为峰值0.48g振幅急剧变化的EL Centro地震波时,基于10~16s时间段的测试数据识别得到的阻尼系数出现负值,说明真实阻尼并不完全符合Rayleigh比例阻尼假定;随矩形窗的前移,参数识别值有所变化(阻尼系数变化较大),表明在真实的震动作用下结构模型实际状态非常复杂。从图8可知,反演的地震动时程与振动台台面实测时程存在较大误差,但前者能够很好地追踪到后者的变化和峰值,这也说明识别出的参数平均值能够反映结构模型在10~16s地震动作用下所处的复杂状态。
结构模型在两种不同输入激励下,识别的结构物理参数有较大差异,分析其可能原因为:输入为小振幅平稳变化的余弦波时,结构模型侧移幅度较小,每层钢板重量基本垂直施压在立柱上并向下传递,大质量钢板在一定程度上约束了立柱,增大了刚度、减小了侧移,试验模型更接近于理想的剪切型结构。输入为大振幅急剧变化的地震波时,结构模型侧移幅度较大且剧烈摇摆,较柔的立柱弯曲角度较大,致使钢板与立柱连接的角钢螺栓发生松动,板柱连接不再是刚性连接,层间有效高度增大、刚度减小,侧移增大,在螺栓松动的情况下,钢板和立柱也会发生碰撞,使试验模型在地震动激励下处于复杂状态。
基于振动台试验测试数据,利用修正的复合反演算法,识别结构物理参数和反演输入,产生误差的原因有:(1)材料误差(实际值与设计值不符);(2)设计误差(节点的角钢螺栓连接影响有效高度等);(3)制作误差(尺寸不准、螺栓不紧等);(4)试验误差(振动台、仪器等产生的误差);(5)计算误差(试验模型理想化、测试噪声、数值模型简化等问题)等。
3 结论
在输入未知条件下,为了识别非线性参数系统,并消除噪声异常点的影响,引入修正Leven-berg-Marquardt法和矩形窗法,建立SVD-mLM法,改进了复合反演算法,数值研究已经验证了改进的复合反演算法的有效性和鲁棒性。本文设计了一个5层单跨钢框架模型,采用改进的复合反演算法,开展了噪声真实存在情形下结构物理参数时域识别和输入反演的振动台试验研究,结果验证了矩形窗法、SVD-mLM法和改进的复合反演算法在识别结构物理参数和反演输入时的可行性和有效性。
对本文的振动台试验结果进行分析,认为试验模型的板柱连接节点需要进一步改进设计,使之更接近于刚性节点,从而使试验模型更近似于理想化的数值模型。

