一种基于张量投票的牙齿特征识别的方法
何嘉琪+何思渊

摘要:在正畸治疗中,牙齿表面特征是非常重要的测量与治疗的参考点。为了快速准确的识别牙齿特征,本文提出了一种基于张量投票的提取算法。该算法通过计算将牙齿三维网格数据拓扑成为半边结构,将输入的每个顶点进行张量编码,根据张量投票矩阵的特征值进行候选特征点的选取。对于候选特征点,通过邻域搜索将其进行聚类,并通过非极大值抑制选取最终的特征。实验结果表明,该方法可以有效识别牙齿表面不同类型的特征,具有较高的准确性和实用性。
关键词:特征提取;半边结构;张量投票;邻域搜索
中图分类号:TP18 文献标识码:A 文章编号:1009-3044(2016)12-0182-03
1 概述
牙齿特征位于牙冠表面,与牙齿的生理学功能密切相关,主要包含牙尖、中央窝、切嵴等。牙冠表面的牙釉质是人体最坚硬的组织结构,这种特征结构在治疗过程中一般不会丢失。牙齿特征是正畸医师评估患者咬合情况的参考点,这些特征的正确接触与排列也是正畸治疗所追求的最终目标。因此,牙齿特征识别对于正畸医师在临床治疗时评估咬合情况以及制定治疗计划都具有非常重要的意义。
目前,临床上一般都会对患者的错颌畸形情况进行Angle错颌分类[1],以便对患者病情进行讨论和研究,并进一步的制订治疗方案。在口腔正畸学的不断发展中,也出现了几种正畸指数,用来评估采取正畸治疗的必要性或者对正畸治疗的效果进行评价。这些指数包括PAR[2](Peer Assessment Rating)指数、ABO-OGS[3](American Board of Orthodontics- Objective Grading System)、IOTN[4](The Index of Orthodontic Treatment Need)指数等。Angle错颌分类主要依据上颌第一磨牙的近中颊尖与下颌第一磨牙近中颊沟之间的位置关系。ABO-OGS指数与PAR指数等评估标准考察的主要对象也是牙尖和沟槽等部位相互的距离与排列情况。因此,从治疗前的诊断与分类,到治疗中的考察,再到治疗完成后的评估,牙齿特征贯穿始终。识别与记录这些特征是正畸中必经的步骤。
Kondo[5]等人提出首先计算牙齿图像中每一点的梯度方向不连续性(the magnitude of the discontinuities in gradient orientation),然后利用阈值来选取特征点,最后通过形态学操作来进行筛选。仲哲等人[6]提出的方法需要计算每个顶点的曲率和需要手工建立每颗牙齿坐标系,并人工选取顶点与坐标轴之间阈值,而阈值选择对提取结果有着很大的影响。王寅等人[7]提出的方法使用了三维SUSAN算法,针对不同位置的不同类型的牙齿和特征都需要选择不同的阈值,无法在牙列上直接提取特征。
目前,市场上主流的商业化的口腔CAD/CAM软件都使用了交互式的牙齿特征提取方法。在CEREC口腔修复系统中,用户需要自行选取一系列的牙齿特征点,在选取过程中,系统会把已经提取的特征点逐个进行优化;3Shape口腔修复系统则需要先在牙根附近定位8个标志点,通过8个标志点粗略定位特征点,随后优化提取出特征点;Dental Wings口腔修复系统将牙齿三维曲面展开到平面中,通过在二维曲面的牙冠区域选取出初始点,计算并得出二维特征线,随后映射回三维曲面得到最终的牙齿特征。
上述几种牙齿特征提取算法与口腔修复系统软件都可以实现牙齿特征的提取,但是他们都要人工干预,需要手动选定一些特征点,或者选取阈值来进行识别。这对使用者的软件使用技能以及对牙齿特征的了解均提出了一定的要求,如果初始人工选定的位置不准确,会影响最终的提取结果。针对上述缺点,我们提出了一种基于改进的张量算法,并结合邻域搜索策略的方法来提取牙齿特征。对于正畸工作者来说,自动快速精准的牙齿表面特征提取技术可以大大降低他们的工作难度与复杂度,提高他们的工作效率。
2 牙冠解剖特征简介
根据口腔解剖学[8],牙齿可以分为切牙、尖牙、前磨牙和磨牙。牙列指的是口腔中全套牙齿的排列模式,上下颌牙列可以分成左右两侧,其中每一侧都包含:两颗切牙,分别是中切牙和侧切牙;一颗尖牙;两颗前磨牙,分别是第一前磨牙和第二前磨牙;三颗磨牙,分别是第一磨牙,第二磨牙和第三磨牙。其中,和尖牙相邻的是第一前磨牙,第二前磨牙则与第一磨牙相邻。切牙和尖牙被称为前牙,作用是切断食物;前磨牙和磨牙统称为后牙,作用是嚼碎食物。
本文涉及的牙冠特征如下:
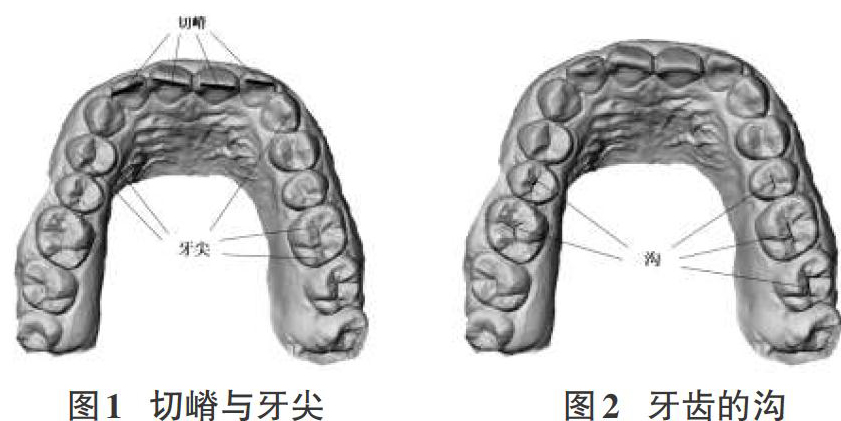
1)切嵴。牙冠表面细长形状的釉质隆起被称为嵴。切嵴是切牙切端舌侧长条形的釉质隆起,具有切割功能。如图1所示。
2) 牙尖。牙冠表面形似椎体的显著的隆起被称为牙尖。尖牙只有一个牙尖,在正畸治疗中该牙尖有着非常重要的作用。在前磨牙和磨牙上,牙尖是牙冠表面角落处的凸起结构。前磨牙通常有二到三个牙尖,磨牙通常有四到五个牙尖,根据所在的牙列和个人情况而定。如图1所示。
3) 沟。沟是牙齿表面位置较低的线状凹陷。如图2所示。
3 三角网格及其拓扑结构
STL格式是一种使用三角片面的集合来表示物体表面形状的数据存储和交换格式。每个三角面片的信息包括三角面片的外法矢以及按右手螺旋法则顺序排列的三个顶点[9]。
由于STL文件只记录了物体表面的几何位置信息,而没有任何几何体之间的拓扑信息,所以在重建实体模型的时候,凭借位置信息来重建拓扑信息是十分关键的步骤。
半边结构是一种使用较为广泛的拓扑重建数据结构。半边结构将三角面片的每一条边分裂为两条方向相反的有向半边,其中法矢符合右手螺旋方向的半边属于当前的三角面片,每个三角面片由三条有向半边组成,而面片之间的连接关系则是通过拓扑半边的相邻半边的指针建立的[10]。在半边结构中,存储了每个顶点的单环邻域顶点与单环邻域面的信息。
虽然半边结构通常比基于边的结构花费更多的存储空间,但半边结构有几项重要的优势:可以得到网格内任意顶点与面的关系;方便存储每条边的信息;提供了获得特定顶点的单环邻点的功能。这些优点在许多三角网格算法中非常重要,可以大大提高计算效率。
4 我们提出的特征提取算法
为了有效识别牙齿特征,我们提出了一种基于张量投票的方法,对顶点分类标准进行了改进,并且使用邻域搜索和非极大值抑制来获得准确的识别结果。
4.1 张量投票算法
张量投票算法是一种主要用来检测图像和图形中显著性结构的算法,它对于三维空间中的微分几何结构有着很强的识别能力。该算法最初基于矢量投票,并逐步得到完善,形成了提取视觉结构的成熟的框架[11]。张量投票算法以下三个步骤:对输入数据进行张量编码,计算投票域和线性投票。每个数据都在一个预先设定的投票域内进行投票,向邻域点传递信息的同时也得到其他点给自己的投票,并将得到的投票编码成一个张量。对投票结果分解之后,可以得到各类特征的显著性,即该张量具有此种特征的置信度[12]。而显著性的直观意义则是能迅速引起观察者视觉上的注意的突出程度。
张量投票算法采用的是线性、非迭代的计算方式,可以同时获得不同种类的特征。另外,该算法所使用的参数只与自身尺度因子有关,所以具有很强的鲁棒性,可以在具有许多噪声的稀疏数据中快速有效的计算并提取出特征。
其中[Ss]、[Sc]和[Sn]分别表示平面显著度、曲线显著度以及角点显著度。各个显著度表示了该张量具有某种特征,也就是位于平面,曲线以及角点处的置信度。
根据特征值的大小,顶点可以被分类成面点、边点和角点三类[15]:当[λ1]的值较大,而[λ2]和[λ3]接近于0的时候,则该顶点是表面点;当[λ1]和[λ2]比较大,且[λ3]接近0的时候,该顶点是边点;当[λ1]、[λ2]和[λ3]的值相近且都大于0 的时候,则被定义成角点。其中,边点和角点都属于特征点。根据这个规则,可以把网格数据中所有的顶点进行分类,属于边点和角点的顶点都被当做张量投票的提取结果。
4.2 改进的张量投票分类方法
牙齿数据不同于普通模型,在牙齿表面实际上并不存在锋利的边缘与拐点,而只是一些起伏变化相对较为剧烈的点和区域。张量投票算法中的分类规则会把磨损较为严重,表面相对平坦的牙齿尖点等部位误判为面点,因此原本的分类方法不适用于牙齿特征提取。
为了识别显著度相对较低,原本会被分类成面点的弱特征点,本文改进了分类规则,分类策略如下:设定两个阈值[α]和[β],当[λ2]小于[β]且[λ3]小于[α]时,将顶点分类为面点;当当[λ2]大于[β]且[λ3]小于[α]时,将顶点分类为边点;当[λ3]大于[α]时,将顶点分类为角点。
4.3 邻域搜索和非极大值抑制
为了获得牙冠表面特征的正确位置,还需要对张量投票提取的结果进行筛选和修正。在三角网格中,特征点指的是可以表达出被测量物体形态特征的一系列点,如角点,边点等。显然,这与牙齿表面的特征结构的定义并不相同。
在提取上颌牙列的牙尖与切嵴这两种凸起特征时, 需要对张量投票得到的候选点进行两次邻域搜索并进行非极大值抑制[16],方法如下。
再对[VF]进行一次非极大值抑制,最终得到的点即为附近的牙齿尖点,而其余候选点则被抑制掉。
提取groove时则采用不同的策略。在上颌牙列中,groove的位置在周围牙尖的上方,提取的目标是垂直坐标较高的点。因此,两次邻域搜索之后NMS抑制的实际上是非极小值点。由于下颌牙列与上颌方向相对,提取下颌特征点时NMS的选取标准与上颌相反。
5 实验
本文使用的数据来自于丹麦3Shape公司的TRIOS扫描系统。该系统采用了光学切片技术,可以在口腔内采集到高分辨率,高精度的牙齿测量数据。输入的牙齿网格数据中包含大量冗余信息,如牙龈,以及口腔内其他部分。为了降低计算时间并且避免提取到不感兴趣的牙齿表面特征,实验中只对牙齿咬合面部分进行特征提取。
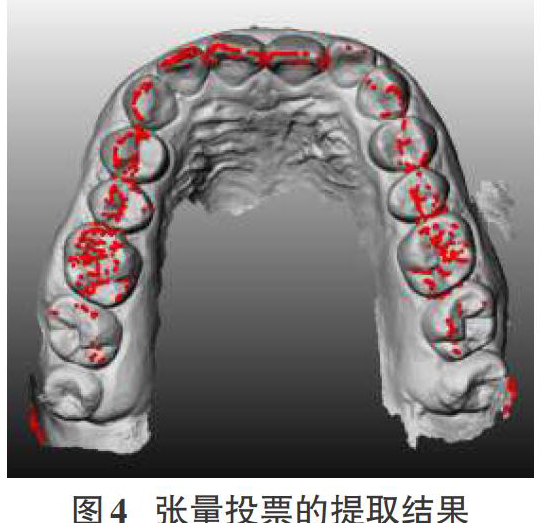
对于采集得到的三维网格牙齿数据进行张量投票,所获得的特征点如图4所示。
图中红色的点表示张量投票提取出的候选特征点。与普通三角网格模型相比,牙齿表面显得非常特殊:形态多变,连续不断的起伏却没有明显的突出点。因此,特征提取的结果中不存在三个特征值相近的角点,而是全部被分类成边点。
对候选特征点进行非极大值抑制操作时,需要设定合适的搜索范围。由于牙齿凸起的部分相对较少,为了得到准确的结果,实验中先搜索了候选点的七环邻域,将邻域内的点进行聚类,并将非极大值抑制。在将新的候选点集内,再进行四环邻域搜索,进行非极大值抑制之后,得到了图5所示的结果。四颗前牙上的红色区域表示切嵴,尖牙,前磨牙和磨牙上的红色点代表牙尖。可以看出,对于前牙的切嵴、前磨牙的双尖点以及磨牙的数个牙尖,该方法都可以有效地进行提取。
在进行中央沟的提取时,为了防止邻域搜索结果非咬合面的点,需要缩小搜索邻域。先搜索候选点的五环邻域,将邻域内的所有点进行非极大值抑制。在将新的候选点集内进行三环邻域搜索,进行非极大值抑制之后,得到的结果如图6所示。
在每颗牙齿靠近中心的位置,红色的点表示提取出的牙冠表面相对位置较低的点,即grooves。值得一提的是,在寻找位置较低的特征点的同时,也获得了牙齿邻接初的一些点。这些点虽然不属于表面特征,但对于牙齿的宽度测量也是非常有用的参考点。
得到这些特征的坐标之后,可以得到牙齿的宽度,咬合时特征点的接触情况,牙齿的倾斜度等信息。正畸医师可以非常方便地对患者牙齿进行安氏分类,描绘牙弓曲线,或使用ABO-OGS等标准对正畸治疗的效果进行评估。
6 结论
我们提出了一种基于改进张量投票算法的牙齿特征提取方法,该方法首先提取出牙齿表面数据中显著度高的点集,然后经过两次邻域搜索-非极大值抑制操作,选取极大值提取出了上颌的牙尖、切嵴与下颌的沟槽,选取极小值提取出了上颌的沟槽和下颌的牙尖、切嵴。与现有的方法相比,我们提出的方法不需要通过人工干预,自动化程度高,可以准确快速的提取正畸医生感兴趣的特征点。
参考文献:
[1] Angle E H. Classification of malocclusion[J]. 1899.
[2] Richmond S, Shaw W C, O'brien K D, et al. The development of the PAR Index (Peer Assessment Rating): reliability and validity[J]. The European Journal of Orthodontics, 1992, 14(2): 125-139.
[3] Casko J S, Vaden J L, Kokich V G, et al. Objective grading system for dental casts and panoramic radiographs[J]. American Journal of Orthodontics and Dentofacial Orthopedics, 1998, 114(5): 589-599.
[4] Shaw W C, Richmond S, O'Brien K D. The use of occlusal indices: a European perspective[J]. American Journal of Orthodontics and Dentofacial Orthopedics, 1995, 107(1): 1-10.
[5] Kondo T, Ong S H, Chuah J H, et al. Robust arch detection and tooth segmentation in 3D images of dental plaster models[C]//Medical Imaging and Augmented Reality, 2001. Proceedings. International Workshop on. IEEE, 2001: 241-246.
[6] Zhong Z. Automatic tooth alignment[D]. Zhejiang University, 2012.
[7] Wang Y. Research on Key Technologies of Orthodontic Treatment Plan Based on Dental Cone-beam [D]. Soutueast University, 2013.
[8] Nelson S J. Wheeler's dental anatomy, physiology and occlusion[M]. Elsevier Health Sciences, 2014.
[9] M?ntyl? M. An introduction to solid modeling[J]. 1988.
[10] Szilv i-Nagy M, Matyasi G Y. Analysis of STL files[J]. Mathematical and Computer Modelling, 2003, 38(7): 945-960.
[11] Medioni G, Lee M S, Tang C K. A computational framework for segmentation and grouping[M]. Elsevier, 2000.
[12] Medioni G, Tang C K, Lee M S. Tensor voting: Theory and applications[J]. Proceedings of RFIA, Paris, France, 2000, 3.
[13] Page D L, Sun Y, Koschan A F, et al. Normal vector voting: crease detection and curvature estimation on large, noisy meshes[J]. Graphical models, 2002, 64(3): 199-229.
[14] Kim H S, Choi H K, Lee K H. Feature detection of triangular meshes based on tensor voting theory[J]. Computer-Aided Design, 2009, 41(1): 47-58.
[15] Shimizu T, Date H, Kanai S, et al. A new bilateral mesh smoothing method by recognizing features[C]//null. IEEE, 2005: 281-286.
[16] Neubeck A, Van Gool L. Efficient non-maximum suppression[C]//Pattern Recognition, 2006. ICPR 2006. 18th International Conference on. IEEE, 2006, 3: 850-855.

