雷诺数对椭圆形断面气动力及驰振稳定性的影响

    马文勇 袁欣欣 尉耀元 刘庆宽

    

    

    

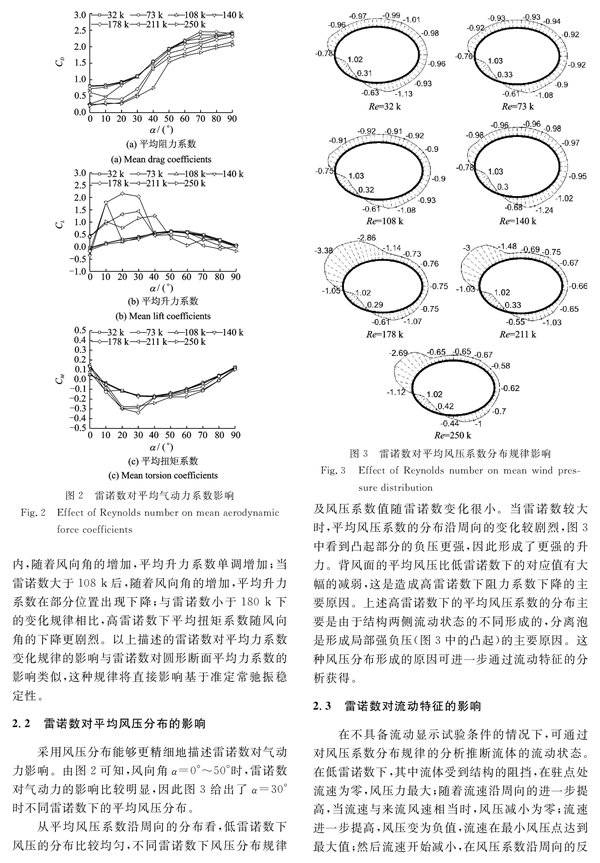
    摘要： 具有类似于圆形断面的细长结构常发生大幅的风致不稳定振动，气动力分析是研究该类振动机理的主要方法，雷诺数是该类结构气动力的主要影响因素之一。通过长短轴之比为1.5的椭圆形断面刚性模型测压风洞试验，得到了雷诺数从32 k～250 k范围内的气动力。讨论了雷诺数对平均气动力、平均风压分布、流动特征点、斯托洛哈数的影响规律。采用考虑雷诺数和振动方向影响的驰振稳定性分析方法，分析了该断面的驰振稳定性。结果表明，在高雷诺数范围内，随着雷诺数的增大平均阻力系数减小、平均升力系数随风向角的变化更剧烈、最小风压点和分离点向尾流移动、规则的漩涡脱落消失；在雷诺数对气动力有明显影响的区域内，气动阻尼为负值，结构可能发生驰振，横风向振动负气动阻尼主要归因于雷诺数对平均气动升力随风向角的变化的影响，顺风向振动负气动阻尼主要是由于平均气动阻力随雷诺数增大而减小造成的。关键词： 风洞试验； 气动力； 椭圆形断面； 雷诺数； 驰振不稳定性

    中图分类号： TU311.3；O351.2文献标志码： A文章编号： 10044523（2016）04073007

    DOI：10.16385/j.cnki.issn.10044523.2016.04.021

    引言

    圆形或者其他无尖角断面形状的柔性索结构常发生风致大幅振动，已经观测到的风致振动形式主要包括涡激共振、驰振、斜拉索风雨振、干索驰振、尾流驰振等。其中干索驰振虽然被Irwin[1]，Flamand[2]，Zuo[3]，Mstsumoto[4]等多次报道，但其受到广泛的认可是在渥太华大学、RWDI（Rowan Williams Davies and Irwin）、加拿大国家研究局和FHWA联合研究并发表了系列研究成果后[511]。

    干索驰振的发生机理有以下三种可能。第一种：干索驰振可能是由索表面的粗糙度或者缺陷引起的气动力变化引起的[5， 10， 12]。换句话说，索不是理想的圆形断面。由于这种缺陷很难量化，因此目前还不清楚引起的大幅振动的机理。第二种：干索驰振是由于风作用在倾斜拉索上产生了气流轴向流动，这种轴向流动抑制了卡门涡的形成，从而诱发了大幅振动[4]。第三种：干索驰振是由于在临界雷诺数下，风与结构产生的某种耦合效应引起的，这种耦合可能与斜拉索表面状态，来流条件等有关[9， 13， 14]。上述三种可能的发生机理都认为，临界雷诺数对干索驰振有重要的影响。

    大量的针对圆形断面气动力的风洞试验和数值研究[1]表明，雷诺数[15]、来流湍流度、表面粗糙度、端部条件等因素都会对圆形断面的气动力产生不同程度的影响。亚临界和超临界被用于描述圆柱阻力系数下降段前和下降段后的流动状态，其中临界区的流动状态和气动力与亚临界区差别很大。现实中诸如斜拉桥拉索等结构其雷诺数常位于临界区[16]且在试验中观测到由于雷诺数引起的大幅振动[17]。Nikitas和Macdonald[9]通过静力和动态试验揭示了雷诺数和斜风向对圆形断面气动力及驰振稳定性的影响，并用此解释干索驰振现象。Alonso[18]认为与圆形断面类似，椭圆形断面也存在雷诺数效应问题。目前雷诺数对圆形断面气动力和振动的研究已经比较丰富，但对于其他无尖角的断面研究仍然比较缺乏，而实际工程中存在大量的非圆形光滑断面，如输电导线覆冰后形成的类似于椭圆形的覆冰形状。另外一个研究椭圆形断面的重要原因是由于椭圆形断面具有和圆形断面类似的雷诺数效应且可以定义明确的风向角，从而克服了圆形断面无法使用经典驰振理论进行驰振稳定性分析的缺点。

    第4期马文勇，等： 雷诺数对椭圆形断面气动力及驰振稳定性的影响振 动 工 程 学 报第29卷雷诺数对气动力的影响机理可以通过对风压分布的深入分析或者流场分析揭示，其中转捩形态和分离点等对是重要的影响参数，目前很多对类似结构的风洞试验都是通过刚性模型测力试验完成的，因此对雷诺数效应产生机理的分析比较缺乏。

    Den Hartog驰振机理常被用于解释驰振现象，这种基于准定常假设的驰振机理揭示了负气动阻尼引起不稳定大幅振动的本质，但未能综合反映振动方向、雷诺数等因素对驰振的影响。Macdonald于2006年提出了一种考虑振动方向、风向角、风偏角和雷诺数的气动阻尼估算方法并将其用于驰振稳定性分析[19]。

    本文采用刚性模型测压试验，得到32 k～250 k雷诺数范围内的长短轴比为1.5椭圆形断面的风压分布，进一步通过流动状态分析给出了雷诺数效应产生的机理，以及雷诺数对风压分布、气动力、斯托罗哈数的影响。采用Macdonald方法分析了振动方向和雷诺数对该椭圆形断面的驰振稳定性的影响。

    Abstract： Wind induced largeamplitude instable vibration occurs on slender cylinder with nonedged crosssection such as circular cylinder. Studies on aerodynamics force on the cylinder have significant contribution to solve prevent the vibration. The Reynolds number is an influencing parameter to determine the aerodynamic force on the cylinder. The rigid model pressure tests in wind tunnel are carried out to obtain the aerodynamic force on cylinder model with elliptical crosssection that ratio of long axis to short axis is 1.5. Effects of the Reynolds number on mean aerodynamic force coefficients， mean wind pressure distribution， flow characteristic points and the Strouhal number are discussed. Considering the effects of Reynolds number and vibration direction， galloping instability is analyzed. The results show， with increasing Reynolds number， mean drag coefficients decrease， variation of mean lift coefficient with the angle of attack become violent， the minimal wind pressure points and separation points move to leeward， the regular vortex shedding disappear； The aerodynamic damping is negative and galloping may happen at the range that the Reynolds number have significant effect on aerodynamic force. The negative aerodynamic damping at crosswind vibration mainly attribute to the effect of the Reynolds number on variation of mean lift coefficient with the angle of attack； the negative aerodynamic damping at along-wind vibration is due to the drag coefficients decrease with an increasing Reynolds number.

    Key words： wind tunnel test； aerodynamic force； elliptical crosssection； the Reynolds number； galloping instability