改进CPM的移动通信用户关系圈挖掘
陈少权 杜翠凤
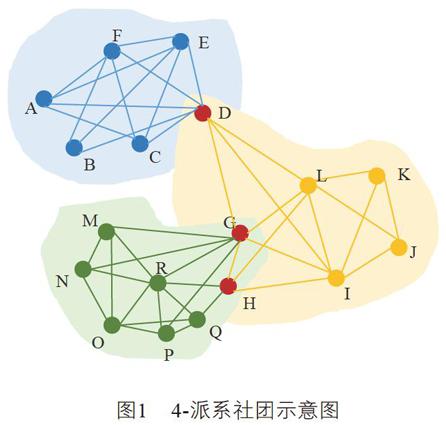

【摘 要】针对现有社团发现算法忽略节点之间的关系强度及其动态性的问题,提出改进CPM算法挖掘移动通信的用户关系圈。首先,采用TF-IDF剔除非重要通话群体;然后,引入时间衰减因子,采用用户通信行为衡量用户之间动态关系强度,结合关系阈值剔除节点之间的弱连接构建大小不同的派系;再次,利用变异系数来衡量派系中用户关系之间的相近性,采用变异系数阈值C.V*剔除关系不紧密的派系;最后,根据用户输入的k值,发现k-派系社团。实验证明,通过重叠社团模块度EQ评测指标验证,该算法的精确度高于传统算法的精确度,具有一定的扩展性。
【关键词】关系强度;时间衰减;关系阈值;变异系数
Relationship Mining of Mobile Communication Users Based on Improved CPM
CHEN Shaoquan, DU Cuifeng
[Abstract] In view of that existing association discovery algorithms ignore the relationship strength and dynamic nature, an improved CPM algorithm is proposed for relationship mining of mobile communication users. First, TF-IDF is used to eliminate unimportant communication groups. Then, the time attenuation factor is introduced and user communication behavior is used to measure the dynamic relationship strength between users. The relationship threshold is used to eliminate the weak connections between nodes to construct different factions of different sizes. Thirdly, the variation coefficient is used to measure the similarity between the user relationships in the factions. The variation coefficient threshold C.V* is used to eliminate the factions which are not closely related. Finally, the k- factional community is found on the basis of the k value input by the user. The experiments prove that the accuracy of the algorithm is higher than that of the traditional algorithm by the EQ evaluation index of overlapping community module degree, and it has a certain extensibility.
[Key words]relationship strength; time attenuation; relationship threshold; coefficient of variation
1 引言
移動通信用户关系圈是根据移动用户的通话关系特征、移动用户的行为特征,对移动用户进行社团划分。这种基于用户特征的划分,能够帮助运营商更加了解用户关系网络的构成,为电信业务的拓展提供科学的支撑。当前有不少成熟的社团划分算法,如Palla等人[1]于2005年首先提出了派系过滤算法(CPM,Clique Percolation Method),该算法突破了传统的非重叠社团划分算法的限制,能够用来分析重叠的社团结构,其分析结果更贴近现实的社团结构。由于CPM的计算复杂度较大,Lancichinetti等人[2]于2009年从网络局部结构的角度出发,提出了基于局部扩展思想的重叠社团挖掘算法(LFM, Local Fitness Measure),提升了社团划分的速度。Evans[3]和Ahn[4]等人突破传统以网络节点为研究对象进行网络划分的局限,提出了边聚类的社团划分方法。Evans将网络结映射成为相应的线图后,可运用非重叠社团发现算法来进行重叠社团的划分。Ahn出了基于边相似度的层次聚类算法来实现重叠社团的划分。上述算法大多考虑节点之间的连接关系,忽略了节点之间关系的强弱,因此所得出的结果一般不满足现实的社团划分需求。因此,相关学者从关系强弱的角度进行了社团划分的研究,如Onnela[5]等人通过提取电信用户网络的权重,利用权重的传播进行社团发现的研究。Kumpula[6]通过移动用户之间的通话行为提取用户关系的权重,基于权重生成模型实现社团结构的提取,实现社团划分。采用文献合作网络进行统计权重分布,根据权重大小对网络的边进行赋值,实现对社团的划分[7]。上述研究算法大多数是基于静态的,而实际生活中用户关系以及用户圈子的划分是动态变化的。除此之外,注重节点之间连接权重的大小而忽略连接权重离散程度的大小,必然会造成一些不合理的节点加入到社团中,不利于真实的社团结构的发现。
本文针对现有社团发现算法忽略节点关系强度及特定社团中用户连接关系变异系数等问题,在CPM算法中引入具有时间衰减效应的权重信息,并通过权重阈值缩小搜索空间降低算法的复杂度,采用权重变异系数来识别真正的社团,剔除一些不合理的节点,提出一种改进CPM的算法来挖掘移动用户关系圈——基于时间衰减因子和关系变异系数的CPM算法。在划分重叠社团后,需要对社团划分质量进行评价以此说明社团划分的合理性,当前重叠社团划分的方法有扩展性模块度函数[8]以及社团连通图评价[9]等方法。由于本文基于用户关系来实现社团划分与联通效率没有可比性,因此采用扩展模块度的方法实现社团划分质量的评价。
交往圈是指移动用户联系频繁且保持较长时间交往的用户群体[10]。本文研究的移动用户通信关系网是基于移动用户的通话详单构建的,由于当前的短信数量较少,因此本文对短信交往不做考虑。将移动用户通话看作移动通信社交网的节点,如果用户之间存在通话关系,则可在用户之间添加一条边,一般可用移动用户之间通话频率以及时长大小来衡量移动用户之间的关系。如果采用上述的通信行为来衡量移动用户的关系,难免将一些公共号码等非重要的通话群体纳入其中,因此,在提取用户的通信交往圈前采用TF-IDF算法来进行数据的预处理。
假设需要对用户u的移动用户交往圈的用户进行分析,C为移动用户u交往圈的用户集合,那么移动用户u交往圈内的其中一位移动用户v的TF-IDF值为:
TF-IDFuv=tfuv×idfuv (1)
其中,tfuv为用户u与用户v的通话频率,idfuv为用户v与所有用户通话的逆频次,等于用户u与用户v的通话次数/用户u与所有用户的通话次数。因此,如果一个用户u与其他用户通话次数越少,那么idfuv值越高,反之亦然。这个值反映一个用户在另一个用户的社交圈子的重要程度,如果用户u与众多用户产生多次通话,那么用户u圈子里面的好友重要程度都不高;相反,如果用户u与某几个用户产生多次通话,那么用户u圈子里面的好友重要性程度较高。TF-IDFuv的数值能够提出一些公众号码、快递号码、中介等号码对用户圈选取的影响,能够在一定程度上保证用户关系圈挖掘算法的精度和速度。
采用TF-IDF算法求出每一个用户之间的TF-IDF值,然后基于设定的TF-IDF阈值进行预处理。TF-IDF阈值的设置是参考Farkas的派系强度函数公式计算得出:
(2)
其中,d(u)表示与用户u产生交往的用户数量,也可理解为用户u的度数。如果用户u和用户v之间的TF-IDF值小于设定的阈值,那么可认为用户v是用户u的非重要通话群体并剔除掉。
3.3 提取满足条件的节点,找到大小不同的派系
移动通信的社交关系网络符合指数为3的幂定律分布的特点[11],个人之间的联系呈现出重力模型的关系。根据这一特点,结合文献[11]得出的结论,在利用TF-IDF值剔除非重要通话群体的基础上,提取网络度数大于2的节点构建满足度数条件的社交网络,缩小派系搜索过程所花费的时间。基于该社交网络,寻找度数最大的用户集合,从该集合中随机抽取一个用户出发,找到包含该用户大小为g-1的派系后,删除该用户以及其连接的用户;再另选一个用户寻找包含该用户大小为g-1的派系,直至集合中没有用户为止。同理,g-1派系、g-2派系、…、k派系的寻找方法按照上述步骤进行,当g=k时,算法停止。
3.4 引用时间衰减因子衡量移动用户之间连接关
系强度
社会网络中的连接关系在特定的网络中具有特定的含义:比如在真实社会网络中表示好友的关系,在移动通信网络中表示具有相当亲密度的用户之间的通话关系。针对通话详单的特点,本文认为用户u和用户v之间的关系强度不仅考虑用户通话的频率以及通话的时长,更应该考虑评价通话行为的时间属性,也就是需要引入时间衰减因子来反映用户关系强度的动态变化特征。用户之间的近期通话行为更能反映当前用户之间的关系强度,而随着时间的推进,越早的通话行为对当前的用户关系的贡献越小,在计算用户关系时需要对其进行更多的折扣。因此,引入时间因子的用户连接关系强度公式为:
(3)
其中,α和γ为常数,k表示用户u和用户v之间的第k次通话,tuv表示用户u和用户v的第k次通话的通话时长,tu是用户u的总通话时长,tu是用户u的总通话时长,n表示用户u和用户v在一段时间内总的通话次数。
3.5 构建基于变异系数的带权派系
对于移动通信的社交网络来说,如果k-派系的两两用户之间的通信行为大于设定的TF-IDF阈值,那么这k个用户就构成一个k-派系。一般来说,派系之间的成员联系应该非常紧密。但是从用户之间的权重来说,很难衡量两两用户之间的紧密程度,通常来说,一个派系连边的权重越相近,则认为派系之间的关系越紧密。很显然,标准差和变异系数都能描述一个派系的权重的相近性。图3展示了3种带权3-派系的情况,边上的数字是根据上述时间衰减因子结合移动用户之间的通话时长得出的权重信息,数值大表示对应用户之间近期的通话行为越频繁或者用户之间近期通话的时间越长。图3反映了3-派系的用户之间的关系强度,图(a)和图(b)相比,图(a)的权重越相近,其标准差或者变异系数都比图(b)小,因此,图(a)的用户u、用户v以及用户x越有可能构成3-派系。
(a)紧密型 (b)松散型
图3 用户u、用户v、用户x构成的3-派系
但是随着用户数量的增加,比如4用户、5用户甚至更多的用户构成更大的派系后,如果采用标准差的方式来设置阈值就显得不合理,随着用户数量的增加,标准差显然越来越大。如果采用标准差的方式来衡量用户关系之间的相近性,肯定无法识别用户数量较多的派系。因此,本文采用通信用户关系变异系数来衡量用户关系的相近性。用户关系变异系数,又称“标準差率”,可以用来衡量移动用户关系的变异程度,能够在某种程度上反映某个社团中用户关系的稳定性,其公式为:
(4)
其中,σ表示该派系中权重的标准差,μ表示改派系中权重的平均值。
在求出每一个派系的变异系数后,借鉴Farkas的派系强度函数计算派系权重变异系数阈值C.V*,其公式为:
(5)
其中,C为派系集合,u和v表示派系,k表示集合中派系的个数。如果c.v小于设定的阈值C.V*,则认为该k节点构成一个基于变异系数的带权派系,否则,忽略该k派系。
3.6 挖掘重叠社团,评价社团划分质量
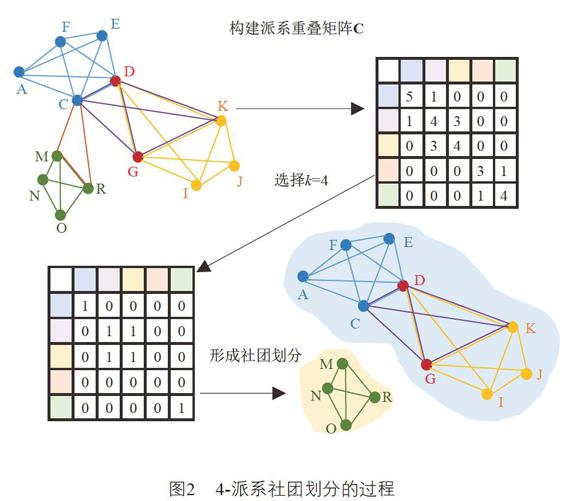
根据上一步找到的基于变异系数的带权派系,建立带权派系重叠矩阵C,根据用户输入的k值,结合带权派系重叠矩阵C,构建带权派系连接矩阵,并发现k-派系社团。如何评价社团划分的合理性是后续的一个重要的问题。扩展模块度是描述某个节点被划分到多个社团后,是否会对重叠社团的扩展模块度函数值产生影响,以此判断节点是否可以被多个社团共享。因此,本文借鉴文献[10]采用扩展模块度函数对重叠社团的划分结果进行评价,其公式为:
(6)
其中,M表示网络中的所有边的权重总和,Oi和Oj分别表示节点i和节点j所属的社团的个数,Wi.表示与节点i有连接的边的权值总和,Wj.表示与节点j有连接的边的权值总和,如果节点i和节点j同属于一个派系,则δ(ci, cj)=1,否则δ(ci, cj)=0。
4 实验效果分析
本文采用的是某地市2016年1月1日至2016年12月30日一年某运营商移动用户的通话详单数据,该数据大小为436 G,包含150多万用户发生通话的基站位置、通话对象、通话日期等相关信息。在下面的实验中,本文重点对比改进后的CPM与传统的CPM算法结果,验证算法对划分移动社交社会网络的可用性。
本文通过分析移动社交网络的属性,发现该社交网络中含有大量的三角形,也就是移动社会网络中大多数的3-派系,因此本文仅仅分析k=3和k=4的算法对比结果,其他k值本文暂时不做考虑。通过图4可以看出,k=3的EQ值总体上高于k=4的EQ值,而且从EQ值的变化趋势可知,当变异系数在[0.5, 0.6]之间变化时,其EQ值趋于稳定的状态。本文采用公式(5)计算的权重变异系数阈值C.V*值0.513 85落在该区间内,实验结论表明,采用Farkas派系强度函数计算派系权重变异系数阈值C.V*的方法是有效的,提升了算法的扩展性。
除此之外,变异系数阈值C.V*体现构成派系条件的苛刻程度,阈值越小,表示模型对派系边权重的离散程度的要求越苛刻,一些真实的社团可能不会被认为是派系,社团划分结果中社团内部连接非常紧密。相反,阈值越小表示模型对派系边权重的离散程度的要求越宽泛,很多不相关的社团可能会被划分进来,社团划分的结果是社团内部连接非常松散。
根据上述流程得出改进后的CPM与传统的CPM算法的EQ值对比结果如图5所示。
由图5可知,改进后CPM算法的EQ评价值高于传统的CPM算法EQ评价值。实验结果表明,改进后的CPM算法经过一系列的数据预处理、阈值设置处理的步骤,能够在很大程度上剔除不合理的节点以及不满足条件的相关派系,能够在很大程度上保证算法所得到的结果符合社团划分的标准。
5 结束语
本文利用移动用户的通信数据提取用户的社交网络,采用改进CPM的算法来实现通信用户关系圈的挖掘。实验表明,在同等的k值情况下,改进的CPM算法经过一系列数据处理后,能够在很大程度上保证算法的精度。除此之外,该算法经过对数据预处理、阈值设置处理等步骤剔除不合理的节点以及不满足条件的相关派系,能够在很大程度上满足海量通信用户社团的划分要求,因此,改进后的CPM算法相比传统的CPM实验法具有更大的扩展优势。
参考文献:
[1] Palla G, Dernyi I, Farkas I, et al. Uncovering the overlapping community structure of complex networks in nature and society[J]. Nature, 2005,435(9): 814-818.
[2] Lancichinetti A, Fortunato S, Kertesz J. Detecting the Overlapping and Hierarchical Community Structure in Complex Networks[J]. New Journal of Physics, 2009(11): 033015.
[3] Evans T, Lambiotte R. Line Graphs, Link Partitions, and Overlapping Communities[J]. Physical Review E, 2009,80(1): 016105.
[4] Ahn Y Y, Bagrow J P, Lehmann S. Link Communities Reveal Multiscale Complexity in Networks[J]. Nature, 2010,466(7307): 761.
[5] Onnela J P, Saramaki J, Hyvonen J, et a1. Structure and tie strengths in mobile communication networks[J]. Proceedings of the National Academy of Sciences, 2007,104(18): 7332-7336.
[6] Kumpula J M, Onnela J P, Saramaki J, et a1. Emergence of communities in weighted networks[J]. Physical Review Letters, 2007,99(22).
[7] 吴文涛,肖仰华,何震瀛,等. 基于权重信息挖掘社会网络中的隐含社团[C]//Ndbc中国数据库学术会议, 2009.
[8] Shen H, Cheng K, Cai M, et al. Detect overlapping and hierarchical community structure in networks[J]. Physica A: Statistical Mechanics and its Applications, 2009,388(8): 1706-1712.
[9] Duan Y, Lu F. Structural robustness of city road networks based on community[J]. Computers Environment and Urban Systems, 2013(41): 75-87.
[10] 蔣仕宝,陈少权. 基于呼叫指纹的重入网识别算法研究[J]. 移动通信, 2016,40(22): 27-30.
[11] 吕明玲. 基于通话记录和短信记录的关系圈挖掘[D]. 广州: 华南理工大学, 2014.



【摘 要】针对现有社团发现算法忽略节点之间的关系强度及其动态性的问题,提出改进CPM算法挖掘移动通信的用户关系圈。首先,采用TF-IDF剔除非重要通话群体;然后,引入时间衰减因子,采用用户通信行为衡量用户之间动态关系强度,结合关系阈值剔除节点之间的弱连接构建大小不同的派系;再次,利用变异系数来衡量派系中用户关系之间的相近性,采用变异系数阈值C.V*剔除关系不紧密的派系;最后,根据用户输入的k值,发现k-派系社团。实验证明,通过重叠社团模块度EQ评测指标验证,该算法的精确度高于传统算法的精确度,具有一定的扩展性。
【关键词】关系强度;时间衰减;关系阈值;变异系数
Relationship Mining of Mobile Communication Users Based on Improved CPM
CHEN Shaoquan, DU Cuifeng
[Abstract] In view of that existing association discovery algorithms ignore the relationship strength and dynamic nature, an improved CPM algorithm is proposed for relationship mining of mobile communication users. First, TF-IDF is used to eliminate unimportant communication groups. Then, the time attenuation factor is introduced and user communication behavior is used to measure the dynamic relationship strength between users. The relationship threshold is used to eliminate the weak connections between nodes to construct different factions of different sizes. Thirdly, the variation coefficient is used to measure the similarity between the user relationships in the factions. The variation coefficient threshold C.V* is used to eliminate the factions which are not closely related. Finally, the k- factional community is found on the basis of the k value input by the user. The experiments prove that the accuracy of the algorithm is higher than that of the traditional algorithm by the EQ evaluation index of overlapping community module degree, and it has a certain extensibility.
[Key words]relationship strength; time attenuation; relationship threshold; coefficient of variation
1 引言
移動通信用户关系圈是根据移动用户的通话关系特征、移动用户的行为特征,对移动用户进行社团划分。这种基于用户特征的划分,能够帮助运营商更加了解用户关系网络的构成,为电信业务的拓展提供科学的支撑。当前有不少成熟的社团划分算法,如Palla等人[1]于2005年首先提出了派系过滤算法(CPM,Clique Percolation Method),该算法突破了传统的非重叠社团划分算法的限制,能够用来分析重叠的社团结构,其分析结果更贴近现实的社团结构。由于CPM的计算复杂度较大,Lancichinetti等人[2]于2009年从网络局部结构的角度出发,提出了基于局部扩展思想的重叠社团挖掘算法(LFM, Local Fitness Measure),提升了社团划分的速度。Evans[3]和Ahn[4]等人突破传统以网络节点为研究对象进行网络划分的局限,提出了边聚类的社团划分方法。Evans将网络结映射成为相应的线图后,可运用非重叠社团发现算法来进行重叠社团的划分。Ahn出了基于边相似度的层次聚类算法来实现重叠社团的划分。上述算法大多考虑节点之间的连接关系,忽略了节点之间关系的强弱,因此所得出的结果一般不满足现实的社团划分需求。因此,相关学者从关系强弱的角度进行了社团划分的研究,如Onnela[5]等人通过提取电信用户网络的权重,利用权重的传播进行社团发现的研究。Kumpula[6]通过移动用户之间的通话行为提取用户关系的权重,基于权重生成模型实现社团结构的提取,实现社团划分。采用文献合作网络进行统计权重分布,根据权重大小对网络的边进行赋值,实现对社团的划分[7]。上述研究算法大多数是基于静态的,而实际生活中用户关系以及用户圈子的划分是动态变化的。除此之外,注重节点之间连接权重的大小而忽略连接权重离散程度的大小,必然会造成一些不合理的节点加入到社团中,不利于真实的社团结构的发现。
本文针对现有社团发现算法忽略节点关系强度及特定社团中用户连接关系变异系数等问题,在CPM算法中引入具有时间衰减效应的权重信息,并通过权重阈值缩小搜索空间降低算法的复杂度,采用权重变异系数来识别真正的社团,剔除一些不合理的节点,提出一种改进CPM的算法来挖掘移动用户关系圈——基于时间衰减因子和关系变异系数的CPM算法。在划分重叠社团后,需要对社团划分质量进行评价以此说明社团划分的合理性,当前重叠社团划分的方法有扩展性模块度函数[8]以及社团连通图评价[9]等方法。由于本文基于用户关系来实现社团划分与联通效率没有可比性,因此采用扩展模块度的方法实现社团划分质量的评价。
交往圈是指移动用户联系频繁且保持较长时间交往的用户群体[10]。本文研究的移动用户通信关系网是基于移动用户的通话详单构建的,由于当前的短信数量较少,因此本文对短信交往不做考虑。将移动用户通话看作移动通信社交网的节点,如果用户之间存在通话关系,则可在用户之间添加一条边,一般可用移动用户之间通话频率以及时长大小来衡量移动用户之间的关系。如果采用上述的通信行为来衡量移动用户的关系,难免将一些公共号码等非重要的通话群体纳入其中,因此,在提取用户的通信交往圈前采用TF-IDF算法来进行数据的预处理。
假设需要对用户u的移动用户交往圈的用户进行分析,C为移动用户u交往圈的用户集合,那么移动用户u交往圈内的其中一位移动用户v的TF-IDF值为:
TF-IDFuv=tfuv×idfuv (1)
其中,tfuv为用户u与用户v的通话频率,idfuv为用户v与所有用户通话的逆频次,等于用户u与用户v的通话次数/用户u与所有用户的通话次数。因此,如果一个用户u与其他用户通话次数越少,那么idfuv值越高,反之亦然。这个值反映一个用户在另一个用户的社交圈子的重要程度,如果用户u与众多用户产生多次通话,那么用户u圈子里面的好友重要程度都不高;相反,如果用户u与某几个用户产生多次通话,那么用户u圈子里面的好友重要性程度较高。TF-IDFuv的数值能够提出一些公众号码、快递号码、中介等号码对用户圈选取的影响,能够在一定程度上保证用户关系圈挖掘算法的精度和速度。
采用TF-IDF算法求出每一个用户之间的TF-IDF值,然后基于设定的TF-IDF阈值进行预处理。TF-IDF阈值的设置是参考Farkas的派系强度函数公式计算得出:
(2)
其中,d(u)表示与用户u产生交往的用户数量,也可理解为用户u的度数。如果用户u和用户v之间的TF-IDF值小于设定的阈值,那么可认为用户v是用户u的非重要通话群体并剔除掉。
3.3 提取满足条件的节点,找到大小不同的派系
移动通信的社交关系网络符合指数为3的幂定律分布的特点[11],个人之间的联系呈现出重力模型的关系。根据这一特点,结合文献[11]得出的结论,在利用TF-IDF值剔除非重要通话群体的基础上,提取网络度数大于2的节点构建满足度数条件的社交网络,缩小派系搜索过程所花费的时间。基于该社交网络,寻找度数最大的用户集合,从该集合中随机抽取一个用户出发,找到包含该用户大小为g-1的派系后,删除该用户以及其连接的用户;再另选一个用户寻找包含该用户大小为g-1的派系,直至集合中没有用户为止。同理,g-1派系、g-2派系、…、k派系的寻找方法按照上述步骤进行,当g=k时,算法停止。
3.4 引用时间衰减因子衡量移动用户之间连接关
系强度
社会网络中的连接关系在特定的网络中具有特定的含义:比如在真实社会网络中表示好友的关系,在移动通信网络中表示具有相当亲密度的用户之间的通话关系。针对通话详单的特点,本文认为用户u和用户v之间的关系强度不仅考虑用户通话的频率以及通话的时长,更应该考虑评价通话行为的时间属性,也就是需要引入时间衰减因子来反映用户关系强度的动态变化特征。用户之间的近期通话行为更能反映当前用户之间的关系强度,而随着时间的推进,越早的通话行为对当前的用户关系的贡献越小,在计算用户关系时需要对其进行更多的折扣。因此,引入时间因子的用户连接关系强度公式为:
(3)
其中,α和γ为常数,k表示用户u和用户v之间的第k次通话,tuv表示用户u和用户v的第k次通话的通话时长,tu是用户u的总通话时长,tu是用户u的总通话时长,n表示用户u和用户v在一段时间内总的通话次数。
3.5 构建基于变异系数的带权派系
对于移动通信的社交网络来说,如果k-派系的两两用户之间的通信行为大于设定的TF-IDF阈值,那么这k个用户就构成一个k-派系。一般来说,派系之间的成员联系应该非常紧密。但是从用户之间的权重来说,很难衡量两两用户之间的紧密程度,通常来说,一个派系连边的权重越相近,则认为派系之间的关系越紧密。很显然,标准差和变异系数都能描述一个派系的权重的相近性。图3展示了3种带权3-派系的情况,边上的数字是根据上述时间衰减因子结合移动用户之间的通话时长得出的权重信息,数值大表示对应用户之间近期的通话行为越频繁或者用户之间近期通话的时间越长。图3反映了3-派系的用户之间的关系强度,图(a)和图(b)相比,图(a)的权重越相近,其标准差或者变异系数都比图(b)小,因此,图(a)的用户u、用户v以及用户x越有可能构成3-派系。
(a)紧密型 (b)松散型
图3 用户u、用户v、用户x构成的3-派系
但是随着用户数量的增加,比如4用户、5用户甚至更多的用户构成更大的派系后,如果采用标准差的方式来设置阈值就显得不合理,随着用户数量的增加,标准差显然越来越大。如果采用标准差的方式来衡量用户关系之间的相近性,肯定无法识别用户数量较多的派系。因此,本文采用通信用户关系变异系数来衡量用户关系的相近性。用户关系变异系数,又称“标準差率”,可以用来衡量移动用户关系的变异程度,能够在某种程度上反映某个社团中用户关系的稳定性,其公式为:
(4)
其中,σ表示该派系中权重的标准差,μ表示改派系中权重的平均值。
在求出每一个派系的变异系数后,借鉴Farkas的派系强度函数计算派系权重变异系数阈值C.V*,其公式为:
(5)
其中,C为派系集合,u和v表示派系,k表示集合中派系的个数。如果c.v小于设定的阈值C.V*,则认为该k节点构成一个基于变异系数的带权派系,否则,忽略该k派系。
3.6 挖掘重叠社团,评价社团划分质量
根据上一步找到的基于变异系数的带权派系,建立带权派系重叠矩阵C,根据用户输入的k值,结合带权派系重叠矩阵C,构建带权派系连接矩阵,并发现k-派系社团。如何评价社团划分的合理性是后续的一个重要的问题。扩展模块度是描述某个节点被划分到多个社团后,是否会对重叠社团的扩展模块度函数值产生影响,以此判断节点是否可以被多个社团共享。因此,本文借鉴文献[10]采用扩展模块度函数对重叠社团的划分结果进行评价,其公式为:
(6)
其中,M表示网络中的所有边的权重总和,Oi和Oj分别表示节点i和节点j所属的社团的个数,Wi.表示与节点i有连接的边的权值总和,Wj.表示与节点j有连接的边的权值总和,如果节点i和节点j同属于一个派系,则δ(ci, cj)=1,否则δ(ci, cj)=0。
4 实验效果分析
本文采用的是某地市2016年1月1日至2016年12月30日一年某运营商移动用户的通话详单数据,该数据大小为436 G,包含150多万用户发生通话的基站位置、通话对象、通话日期等相关信息。在下面的实验中,本文重点对比改进后的CPM与传统的CPM算法结果,验证算法对划分移动社交社会网络的可用性。
本文通过分析移动社交网络的属性,发现该社交网络中含有大量的三角形,也就是移动社会网络中大多数的3-派系,因此本文仅仅分析k=3和k=4的算法对比结果,其他k值本文暂时不做考虑。通过图4可以看出,k=3的EQ值总体上高于k=4的EQ值,而且从EQ值的变化趋势可知,当变异系数在[0.5, 0.6]之间变化时,其EQ值趋于稳定的状态。本文采用公式(5)计算的权重变异系数阈值C.V*值0.513 85落在该区间内,实验结论表明,采用Farkas派系强度函数计算派系权重变异系数阈值C.V*的方法是有效的,提升了算法的扩展性。
除此之外,变异系数阈值C.V*体现构成派系条件的苛刻程度,阈值越小,表示模型对派系边权重的离散程度的要求越苛刻,一些真实的社团可能不会被认为是派系,社团划分结果中社团内部连接非常紧密。相反,阈值越小表示模型对派系边权重的离散程度的要求越宽泛,很多不相关的社团可能会被划分进来,社团划分的结果是社团内部连接非常松散。
根据上述流程得出改进后的CPM与传统的CPM算法的EQ值对比结果如图5所示。
由图5可知,改进后CPM算法的EQ评价值高于传统的CPM算法EQ评价值。实验结果表明,改进后的CPM算法经过一系列的数据预处理、阈值设置处理的步骤,能够在很大程度上剔除不合理的节点以及不满足条件的相关派系,能够在很大程度上保证算法所得到的结果符合社团划分的标准。
5 结束语
本文利用移动用户的通信数据提取用户的社交网络,采用改进CPM的算法来实现通信用户关系圈的挖掘。实验表明,在同等的k值情况下,改进的CPM算法经过一系列数据处理后,能够在很大程度上保证算法的精度。除此之外,该算法经过对数据预处理、阈值设置处理等步骤剔除不合理的节点以及不满足条件的相关派系,能够在很大程度上满足海量通信用户社团的划分要求,因此,改进后的CPM算法相比传统的CPM实验法具有更大的扩展优势。
参考文献:
[1] Palla G, Dernyi I, Farkas I, et al. Uncovering the overlapping community structure of complex networks in nature and society[J]. Nature, 2005,435(9): 814-818.
[2] Lancichinetti A, Fortunato S, Kertesz J. Detecting the Overlapping and Hierarchical Community Structure in Complex Networks[J]. New Journal of Physics, 2009(11): 033015.
[3] Evans T, Lambiotte R. Line Graphs, Link Partitions, and Overlapping Communities[J]. Physical Review E, 2009,80(1): 016105.
[4] Ahn Y Y, Bagrow J P, Lehmann S. Link Communities Reveal Multiscale Complexity in Networks[J]. Nature, 2010,466(7307): 761.
[5] Onnela J P, Saramaki J, Hyvonen J, et a1. Structure and tie strengths in mobile communication networks[J]. Proceedings of the National Academy of Sciences, 2007,104(18): 7332-7336.
[6] Kumpula J M, Onnela J P, Saramaki J, et a1. Emergence of communities in weighted networks[J]. Physical Review Letters, 2007,99(22).
[7] 吴文涛,肖仰华,何震瀛,等. 基于权重信息挖掘社会网络中的隐含社团[C]//Ndbc中国数据库学术会议, 2009.
[8] Shen H, Cheng K, Cai M, et al. Detect overlapping and hierarchical community structure in networks[J]. Physica A: Statistical Mechanics and its Applications, 2009,388(8): 1706-1712.
[9] Duan Y, Lu F. Structural robustness of city road networks based on community[J]. Computers Environment and Urban Systems, 2013(41): 75-87.
[10] 蔣仕宝,陈少权. 基于呼叫指纹的重入网识别算法研究[J]. 移动通信, 2016,40(22): 27-30.
[11] 吕明玲. 基于通话记录和短信记录的关系圈挖掘[D]. 广州: 华南理工大学, 2014.

