基于自适应最稀疏时频分析的阶次方法及应用
程军圣 李宝庆 彭延峰 吴占涛 杨宇

摘要: 自适应最稀疏时频分析(Aadaptive and Sparsest TimeFrequency Analysis,ASTFA)是一种新的时频分析方法,该方法将信号分解转化为最优化问题,在优化的过程中实现信号的自适应分解。为解决ASTFA方法初始相位函数的选择问题,采用了分辨率搜索改进的ASTFA方法,并进一步结合阶次分析方法提出了基于ASTFA的阶次方法。该方法首先采用改进的ASTFA方法对原始信号进行分解同时获得分量的瞬时幅值,然后对瞬时幅值进行阶次分析从而提取故障特征信息。将该方法应用于变速齿轮传动过程中的时变非平稳振动信号的分析与处理,仿真与实验分析表明该方法能够准确提取变速齿轮的故障特征信息,具有一定的优越性。
关键词: 自适应最稀疏时频分析;故障诊断;齿轮;阶次分析;时变非平稳信号
中图分类号: TN911.7; TH165+.3 文献标志码: A 文章编号: 1004-4523(2016)03-0542-07
DOI:10.16385/j.cnki.issn.10044523.2016.03.021
引 言
通过对振动信号进行分析与处理以提取相关信息已成为故障诊断与设备状态监控等领域常用的技术手段。对于齿轮传动,其升降速过程的振动信号包含了丰富的状态信息,一些在平稳运行时不易反映的故障特征可能会充分地表现出来[1],因此对齿轮升降速过程的振动信号进行分析对于齿轮的故障诊断是非常有意义的。工程上,一般采用阶次分析方法来实现时变非平稳信号的平稳化,它可以将齿轮变速过程中产生的与转速有关的振动信号有效地分离出来,同时对与转速无关的信号起到一定的抑制作用[2]。当齿轮发生故障时,其振动信号具有多分量的调幅调频特性,因此在阶次分析之前还需要将其分解为若干个单分量的调幅调频信号之和。目前广泛使用的分解方法是EMD方法,其通过多次迭代将信号分解为一系列具有不同时间尺度的内禀模态函数(Intrinsic Mode Function,IMF)之和,并通过Hilbert变换得到分量信号的瞬时频率和瞬时幅值[3],然后对得到的瞬时幅值进行阶次分析。实际上,这个过程是基于EMD的包络阶次谱方法,其首先进行EMD分解,然后采用Hilbert包络解调方法对调幅调频信号进行处理以提取调幅特征[4],最后对包络信号进行阶次分析。EMD方法自提出后已广泛用于结构分析、设备诊断等各个研究领域,取得了较好的效果[5]。但是EMD方法缺少理论模型和数据基础,在应用上还会产生过包络、欠包络、模态混淆等问题[6]。另外,采用Hilbert包络解调方法对调幅调频信号进行处理以提取调幅特征,会由于Hilbert变换而产生的负频率问题[7]。
受近年来发展的压缩感知理论以及EMD方法的启发,THOMAS Y HOU和Zuoqiang SHI于2011年提出了一种自适应最稀疏时频分析(ASTFA)方法[89],主要思想是基于高斯牛顿迭代法解决非线性优化问题从而实现信号的分解,通过寻找原信号的最稀疏表示,将信号分解问题转化为非线性优化问题。ASTFA与EMD方法不同,ASTFA在目标优化的过程中实现信号的自适应分解,并直接得到各分量的瞬时频率和瞬时幅值,从而获得原始信号完整的时频分布。ASTFA具有明确的数学基础[10],而且不需要进行Hilbert变换就可以直接得到各分量的瞬时频率和瞬时幅值,避免了使用Hilbert变换产生的负频率问题[7]。但是,ASTFA使用了高斯牛顿迭代方法来解决非线性优化问题,因此其对初始相位函数的选择非常敏感,本文采用一种基于分辨率搜索初值的ASTFA方法以实现自适应的寻找最优的初值范围。
本文将改进的ASTFA方法与阶次分析方法相结合提出了基于ASTFA的阶次分析方法。首先采用改进的ASTFA方法对原始信号进行分解同时获得各分量的瞬时幅值,再对瞬时幅值进行阶次分析得到局部特征信息。将该方法应用于变速工况下存在故障的齿轮振动信号的分析与处理,结果表明该方法能够有效提取相应的故障特征信息,适宜于处理时变非平稳信号。
4 应用实例
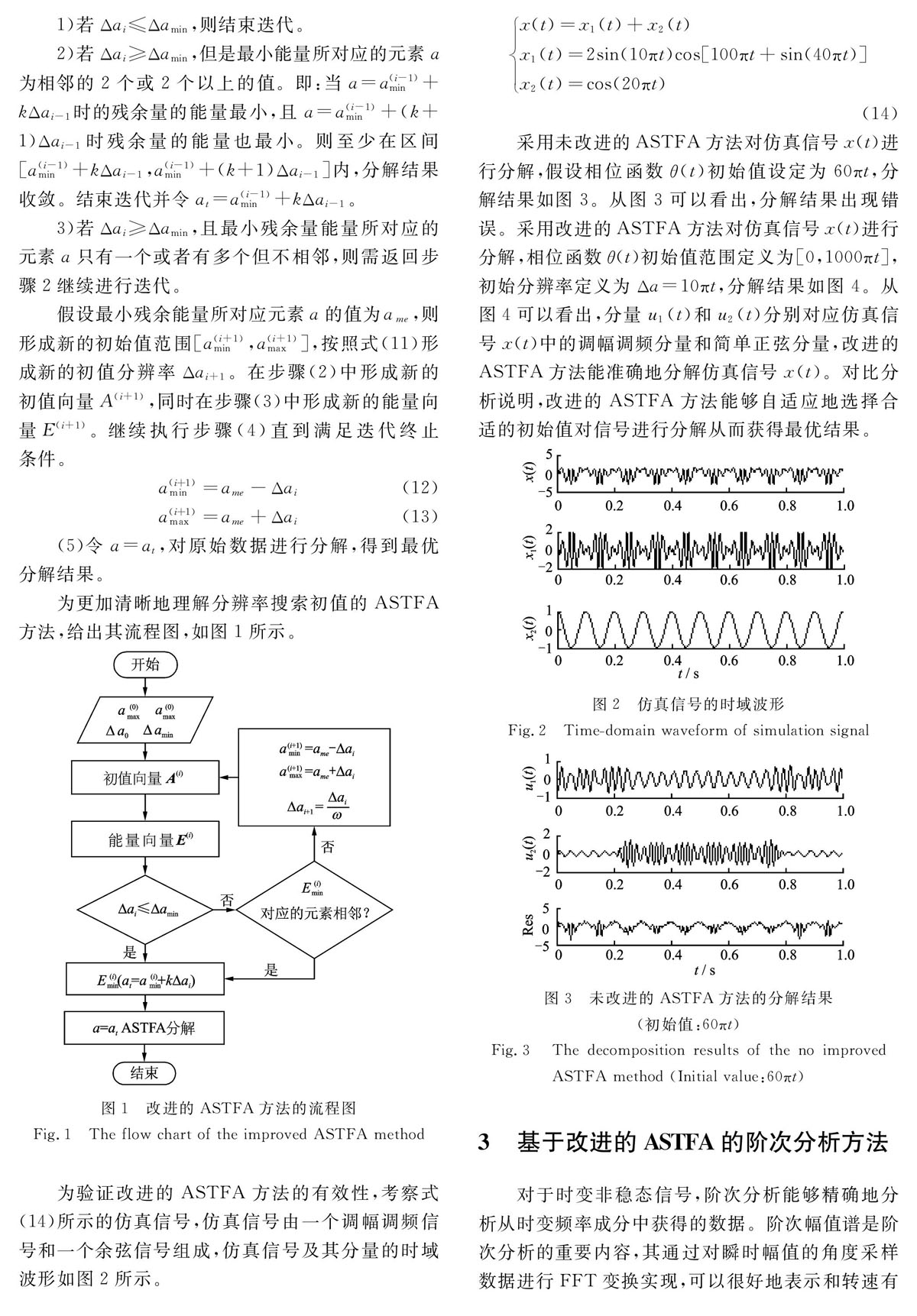
故障齿轮在变速过程中的振动信号是明显的时变非稳态信号,为验证基于ASTFA的阶次方法对时变非稳态信号的处理能力,将其应用于变速工况下齿轮振动信号的处理。在实验台上进行断齿齿轮的瞬态实验,采用模数为2 mm,齿数为55的两个标准直齿轮。在齿轮箱上采集加速度振动信号,通过光电转速传感器采集转速信号,采样频率为8192 Hz,采样时长为1 s。主轴转速变化如图9所示,振动加速度信号如图10所示。
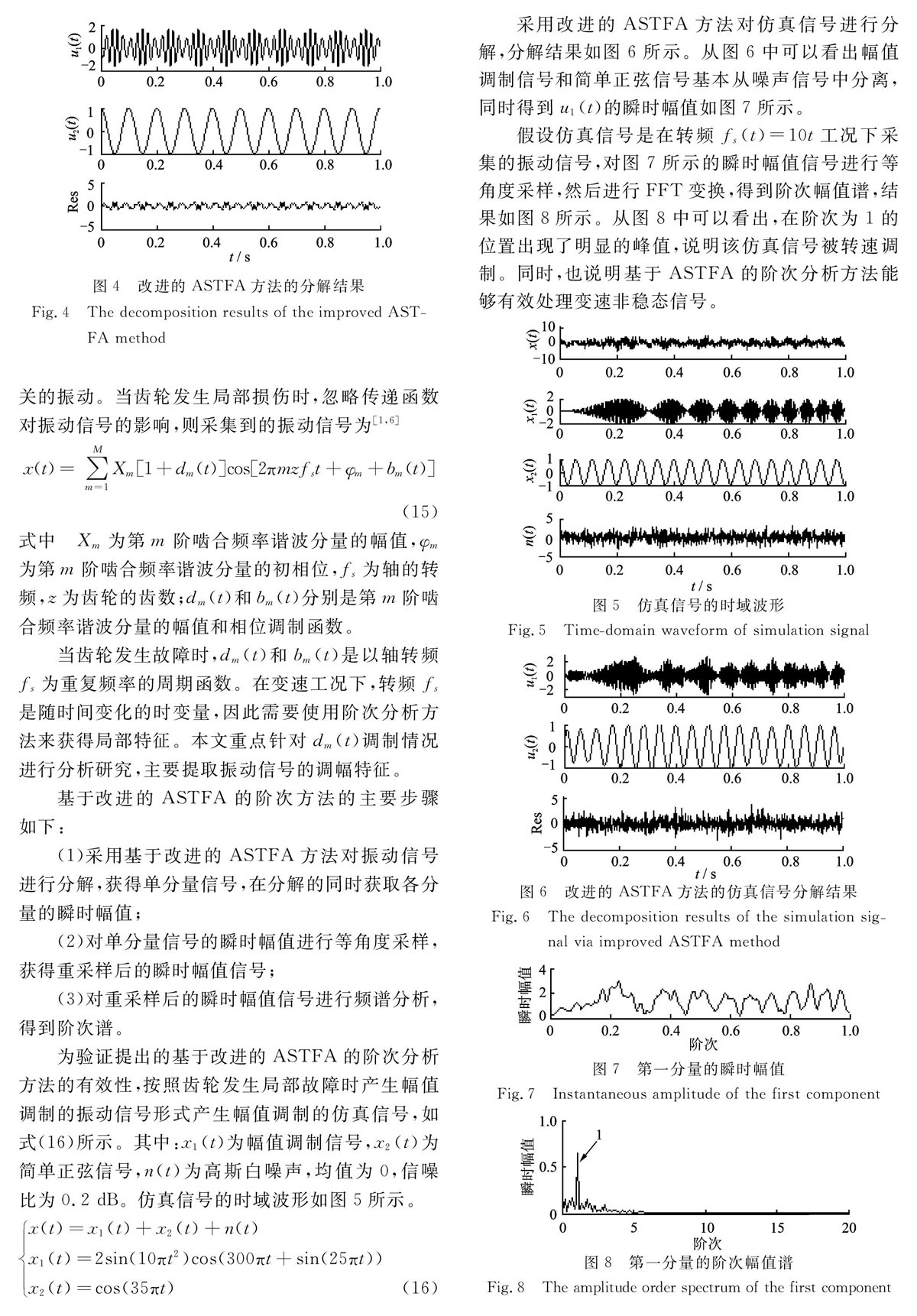
采用改进的ASTFA方法对图10所示的振动信号进行分解,分解结果如图11所示,分解获得两个分量信号以及残余分量。在信号分解的过程中可以同时获得两个分量信号的瞬时幅值,各分量的瞬时幅值如图12所示。
对图12所示的瞬时幅值信号进行阶次分析,得到阶次谱,如图13,14所示。图13为第一分量的阶次谱,图14为第二分量的阶次谱。从图13可以看出,第一分量信号的瞬时幅值阶次谱在阶次为1的位置存在非常明显的峰值,符合断齿齿轮的振动信号幅值调制现象[1,6]。从图14中可以看出,第二分量信号的瞬时幅值阶次谱并无明显的故障特征现象。
为验证ASTFA方法的有效性,对图10所示的原始振动加速度信号进行包络阶次谱分析。首先对原始振动信号进行Hilbert变换获得其包络谱,然后对包络谱进行阶次分析获得其包络阶次谱,分析结果如图15所示。从图15中可以看出,原始振动信号的包络阶次谱并无明显的故障特征现象。这是由于齿轮发生故障时的振动信号表现为多分量的调幅调频信号,因此在进行阶次分析前需将其分解为单分量信号。
为验证基于ASTFA的阶次方法的有效性,对图10所示的振动信号采用基于EMD的包络阶次谱方法进行分析。首先采用EMD方法进行分解,得到3个分量信号,计算各分量信号基于Hilbert变换的包络信号,对包络信号进行阶次分析。为方便,本文直接给出分解得到的3个分量信号的包络阶次谱,如图16~18所示。
从图16~18可以看出,采用EMD分解后的各分量的包络阶次谱中并没有明显的故障特征现象。
对比分析表明,ASTFA方法不但可以将信号分解为单分量的调幅调频信号,而且在分解中直接得到瞬时幅值,避免了基于Hilbert变换的包络分析,因此具有一定的优越性。实验分析结果表明基于ASTFA的阶次分析方法能够准确提取变速齿轮的故障特征信息,适用于处理时变非平稳信号。
5 结 论
根据本文的研究,可以得到以下结论:
(1)ASTFA方法是一种新的自适应时频分析方法,可以用于非平稳、非线性信号的处理。改进的ASTFA方法降低了初始值的选择难度,极大地提高了ASTFA的实际应用性。
(2)包含在振动信号中的局部特征信息一般都具有调幅调频特性,ASTFA方法可以直接得到分量的瞬时幅值和瞬时频率,与EMD等方法不同,ASTFA方法不需进行Hilbert变换,因此,ASTFA方法在处理调幅调频信号方面具有一定的优越性。
(3)基于ASTFA的阶次分析方法可以用于处理时变非平稳信号,特别是对于转速变化的旋转机械,其能够准确从振动信号中提取局部特征信息。
本文重点研究了时变非平稳信号的调幅特征提取,随着研究的深入可以继续研究ASTFA方法在相位调制中的应用。另外,在初始值优化选择方面可以进一步考虑随机优化方法。
参考文献:
[1] 陈向民,于德介,李蓉.基于阶次解调谱的变速齿轮箱复合故障诊断方法[J].振动工程学报,2013,26(6):951—959.
Chen Xiangmin,Yu Dejie,Li Rong.A compound faults method for variationalspeed gearbox based on order tracking demodulation spectrum[J].Journal of Vibration Engineering,2013,26(6):951—959.
[2] 康海英,栾军英,郑海起,等.基于阶次跟踪和经验模态分解的滚动轴承包络解调分析[J].机械工程学报,2007,43(8):119—122.
Kang Haiying, Luan Junying, Zheng Haiqi, et al. Envelope demodulation analysis of bearing based on order tracking and empirical mode decomposition[J]. Journal of Mechanical Engineering, 2007, 43(8):119—122.
[3] Huang N E,Shen Z,Long S R.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J].Proceedings of the Royal Society A,1998,454:903—995.
[4] 程军圣,李宝庆,杨宇,等.基于广义解调时频分析的包络阶次谱在齿轮故障诊断中的应用[J].振动工程学报,2009,22(5):467—473.
Cheng Junsheng, Li Baoqing,Yang Yu, et al. Application of the envelope order spectrum based on the generalized demodulation timefrequency analysis to the gear fault diagnosis[J]. Journal of Vibration Engineering, 2009, 22(5):467—473.
[5] 杨宇,于德介,程军圣.基于经验模态分解的滚动轴承故障诊断方法[J].中国机械工程,2004,15(10):908—920.
Yang Yu,Yu Dejie,Cheng Junsheng.Roller bearing fault diagnosis method based on EMD[J] .China Mechanical Engineering,2004,15(10):908—920.
[6] Lei Y G, Lin J, He Z J,et al.A review on empirical mode decomposition in fault diagnosis of rotating machinery [J].Mechanical Systems and Signal Processing,2013,35(12):108—126.
[7] 任达千,杨世锡,吴昭同,等.信号瞬时频率直接计算法与Hilbert变换及Teager能量法比较[J].噪声与振动控制,2013,49(9):42—48.
Ren Daqian,Yang Shixi,Wu Zhaotong,et al.Comparison of instantaneous frequency directed computing method and Hilbert transform and Teager energy method [J].Journal of Mechanical Engineering,2013,49(9):42—48.
[8] Hou T Y, Shi Z Q.Adaptive data analysis via sparse timefrequency representation [J].Advances in Adaptive Data Analysis,2011,3(1, 2):1—28.
[9] Hou T Y, Shi Z Q.Datadriven timefrequency analysis [J].Applied and Computational Harmonic Analysis,2013,35(2):284—308.
[10] Hou T Y, Shi Z Q, Tavallali P.Convergence of a datadriven timefrequency analysis method [J].Applied and Computational Harmonic Analysis,2014,37(2):235—270.
[11] Mascarenas D, Cattaneo A, Theilere J,et al.Compressed sensing techniques for detecting damage in structures[J].Structural Health Monitoring,2013,12(4):325—338.

