基于相位对齐的毫米波重叠子阵列混合预编码算法
许志斌 郭越红 李立欣


2017年12月3GPP完成了非独立组网(NSA)的5G新空口标准,同时计划在2018年6月完成独立组网(SA)的5G新空口标准,这将为5G商用铺平道路。传统的移动通信网的空口是一个以基站为中心的无线接入系统,而5G的空口将是以用户为中心的接入网,以接入云的形式强化了接入控制功能。另外,5G接入网将基带处理单元(BBU)的功能分解为分布单元(DU)和集中单元(CU),在原来的回传光传输系统基础上增加了前传和中传的环节。基站的大规模天线使得接入传输链路带宽可能达到100 Gb/s量级,而且传统的时分复用传输格式将会被基于低时延高效率的以太网技术取代。
——中国工程院院士邬贺铨
【摘 要】为了进一步解决MIMO系统中射频链路复杂度和系统性能相互制约的问题,重点研究了毫米波多用户大规模MIMO系统下行链路混合预编码设计方案,提出了一种基于相位对齐的重叠子阵列架构混合预编码算法(HB-PA算法)。该算法能够有效地减少射频链路的数量,同时频谱效率可以逼近全数字预编码的性能。通过仿真对比,该方案在硬件复杂度和系统性能等方面,比传统的典型混合预编码算法及基带数字预编码算法能够更有效地实现性能折中。
【关键词】混合预编码;重叠子阵列;毫米波;大规模MIMO
Phase Alignment Based Overlapped Sub-array Hybrid Precoding Algorithm for Millimeter-Wave Systems
XU Zhibin, GUO Yuehong, LI Lixin
(School of Electronics and Information, Northwestern Polytechnical University, Xi'an 710129, China)
[Abstract] In this paper, in order to solve the problem of restraint interacting between hardware complexity and system performance, the hybrid precoding architecture based on overlapped sub-array is studied. A hybrid precoding algorithm called HB-PA based on phase alignment with overlapped sub-array architecture is proposed. The proposed algorithm can effectively reduce the number of radio frequency links, while its spectral efficiency can approach the performance of full digital precoding. Simulation results demonstrate that, compared with the traditionally typical hybrid precoding and the baseband digital precoding algorithms, the proposed algorithm can more effective achieve the performance tradeoff between hardware complexity and system performance.
[Key words]hybrid precoding; overlapped sub-array; millimeter-wave; massive MIMO
1 引言
随着智能设备的不断增多以及新兴多媒体应用的不断出现,移动数据流量呈现出爆炸性增长。具备广域覆盖、高容量、低功耗和低时延等特点的5G技术目前受到了全世界的广泛关注[1]。一些主要国家及相关的行业委员会已经启动了5G项目。例如,美国的5G Americans、日本的ARIB Activities、中国的863-5G Promotion Group、韩国的5G论坛以及全球最大的欧盟研究和创新项目“地平线2020”计划[2]等为5G-PPP(The 5G Infrastructure Public Private Partnership,5G政府民间合作计划)提供资金,为无处不在的5G通信基础设施提供解决方案、架构、技术和标准。
5G的主要技术[3]包括大规模MIMO(Multiple-Input Multiple-Output,多輸入多输出)、HetNets(Heterogeneous Networks,异构网络)、mmWave(Millimeter-Wave,毫米波)通信、FD(Full Duplex,全双工)通信、C-RANS(Cloud-Radio Access Networks,云无线接入网络)、D2D(Device-to-Device,设备到设备)通信、新型多址接入技术、新型信道编码技术、能量感知通信以及能量收割技术等。作为关键技术之一的大规模MIMO技术,在基站或者用户端部署大量天线,根据天线波阵相干叠加原理,将发射功率集中在空间较小的区域,可以在发射机或接收机处实现多种性能增益,如复用增益、分集增益和天线增益。
无线数据通信近年来的显著增长推动了探讨无线电频谱中合适频带的研究。目前6 GHz以下微波频段的频谱资源日益紧缺,终将无法满足人们对更高数据传输速率的需求。毫米波是5G最重要的技术之一[4]。5G拟采用30 GHz~300 GHz的毫米波频段来为存在直达路径下的热点地区提供大容量覆盖和高速率支持。然而,在相同的传播环境下,毫米波容易受到氧气、水汽等的影响,导致传播损耗较大,同时降水、沙尘的负面影响也不可忽略。但是,由于毫米波的波长较小,毫米波元器件(比如天线)的尺寸相对于传统微波通信元器件要小得多,从而在相同的天线孔径总面积下可以部署更多数量的天线,实现大型天线阵列的集成,并且能够通过预编码技术来获得较大的天线阵列增益以补偿毫米波在极高频段下的严重路径损耗,从而改善传输质量。因此,毫米波与大规模MIMO技术的结合被视为5G最有前景的技术之一,而设计高效和稳健的预编码方案已成为当务之急。
在无线通信系统传输过程中,一般通过使用RF(Radio Frequency,射频)链路(其主要器件包括数模转换器、混频器和功率放大器等)对经过预处理的基带信号进行调制后再通过天线进行发射。然而,对于采用大型天线毫米波的系统而言,数字基带预编码是非常复杂和昂贵的,因为每个天线元件不仅需要专用的RF链路,还需要满足模拟前端射频电路的高动态范围。而模拟预编码方法虽然实现起来比较简单且成本较低,但是不够灵活,且波束导向精度相对较低。为了解决这些问题,文献[5]提出采用有限数量的RF链路预编码技术来实现硬件成本和系统性能的折中,从此混合预编码的概念被提出并迅速成为无线通信的一个研究热点。根据RF链路与发射天线之间的连接方式,在大规模MIMO混合预编码系统中有两种典型的系统架构:子阵列架构和全阵列架构。在全阵列架构中,阵列天线元连接到所有射频链上,而子阵列架构中的阵列天线元仅连接到某一特定射频链上[6]。
目前已有论文研究了基于全阵列架构的混合预编码算法。文献[5]在考虑毫米波信道空间稀疏特性的基础上,提出了一种正交匹配跟踪算法。文献[7]提出了一种基于MMSE(Minimum Mean-Square Error,最小均方误差)的混合预编码算法,并在拉格朗日算法的约束条件下得到了封闭解。文献[8]中提出的混合预编码方案在RF域中应用相位控制方法以获得有效信道矩阵,在基带处通过有效信道矩阵执行低维ZF(Zero-Forcing,破零)预编码。然而关于子阵列架构的预编码算法的研究相对较少。文献[9]中利用连续干扰消除来优化每个子阵列的容量。Song等人于2017年在文献[10]中首次提出了一种高效的混合预编码架构——重叠子阵列架构,即相邻子阵之间相互重叠,并采用一种重叠子阵架构下基于贪婪截断功率(Greedy Truncated Power,GTP)的多用户混合预编码算法。由于不同的混合预编碼架构具有各自的特点,因此,如何在不同混合预编码架构下设计硬件复杂度低、频谱效率高的混合预编码算法仍是目前混合预编码技术研究工作中需要攻克的难点。
本文针对上述问题,在毫米波多用户大规模MIMO下行链路系统中,提出了一种基于相位对齐(Phase Alignment,PA)的重叠子阵列架构混合预编码算法。首先通过提取下行链路信道矩阵共轭转置的部分相位信息来设计模拟预编码矩阵,从而实现信道元素的相位对齐,以获取大规模MIMO系统所提供的高阵列增益。在得到模拟预编码矩阵后,进而可以得到系统的射频等效信道矩阵,然后采用ZF算法求取数字预编码矩阵,最终实现混合波束形成方案的设计。与全阵列架构预编码方案相比,本文所提出的算法具有更高的频谱效率和更低的硬件实现复杂度。
2 系统模型
2.1 系统模型
毫米波多用户大规模MIMO混合预编码系统框图如图1所示。发射端将Ns个数据流发送到接收端Nt根天线上。发射端的数据流在基带上通过一个数字预编码器FBB处理后,再通过NRF个射频链路,最后经过一个模拟预编码器FRF,其中模拟预编码器一般通过模拟移相器实现。在全阵列架构中(如图2(a)所示),每个发射天线都连接到所有RF链路,这将导致很高的硬件实现复杂度以及成本开销。而在非重叠子阵列架构中(如图2(b)所示),每个发射天线仅连接到一个RF链路,连接在同一个RF链路的天线阵列称之为一个子阵列,且非重叠子阵列架构中所需模拟移相器的数量等于发射天线的数量。与全阵列架构相比,非重叠子阵列架构降低了模拟预编码过程中所需模拟移相器的数量和硬件实现复杂度,代价是部分频谱效率会有所降低。为了在系统性能和硬件实现复杂度之间做出折中,本文综合考虑了重叠子阵架构(如图2(c)所示)。所谓重叠子阵架构,就是相邻子阵之间存在重叠现象,基于该架构的混合波束形成系统在保持相对较低的复杂度的同时能够获得更高的阵列增益。
图2 三种不同类型的架构模型
在重叠子阵列架构中,每个基站存在NRF个子阵,假设每个子阵有相等的天线数Nsub,接收端为K个用户,相邻子阵重叠的天线数为ΔM。在图2(c)的例子中,RF链的个数为NRF=2,子阵的数量与RF链的数量相等,每个子阵的天线数量均为Nsub=4,而重叠天线数ΔM=2。当ΔM=0时,该重叠子阵架构转化为非重叠子阵架构,而当ΔM=Nsub时,该重叠子阵架构转化为全阵列架构。针对图1所示的多用户混合预编码系统,假设基站第K个子阵发送数据给第K个用户,则有Ns=NRF=K。由于用户均配置单天线,所以在接收端不需要对接收到的信号作进一步的合并处理,只需设计模拟预编码矩阵FRF和数字预编码矩阵FBB即可。其中,FBB仍可表示为FBB=[fBB1, fBB2, …, fBBK],而FRF表示为:
(1)
其中,是模拟预编码
矩阵FRF里面的非零权值,它们的模值满足。通过限制来标准化发射机的总发射功率,信道采用28 GHz的毫米波信道模型,为了充分利用大规模MIMO的特性,假设用户可以获取完美的信道状态信息。
2.2 信道模型
众所周知,与具有丰富散射体环境的低频信道不同,毫米波波段中的高路径损耗导致有限的空间选择性。为了体现毫米波信道稀疏散射体的特性,采用Saleh-Valenzuela信道模型来反映其散射特性[11]。毫米波信道模型如图3所示。假设用户k的信道具有L个散射体,则基站与用户k之间的信道矩阵可以表示为:
(2)
其中,gkl是用户k的第l路径的增益。Nr表示用户接收天线的个数。aHt(θkl)和ar(φkl)分别表示基站和用户终端的天线阵列响应矢量。为不失一般性,本文中使用ULA(Uniform Linear Array,均匀线性阵列)。θkl和φkl分别表示从发射机到用户k的第l路径的离开角和到达角,它们均遵循[0, 2π]的均匀分布。aHt(θkl)和ar(φkl)可以分别表示为:
(3)
(4)
其中,λ表示波长,d表示天线之间的距离,其中d=λ/2。
图3 毫米波信道模型
3 基于重叠子阵列的混合预编码设计
对于图1中的混合预编码的系统模型,用户k的接收信干噪比(SINR,Signal to Interference Plus Noise Ratio)被定義为SINRk,为高斯白噪声,SINRk可以表示为:
(5)
系统频谱效率用符号R表示,其表达式为:
(6)
在大规模MIMO系统中,每个天线需连接到特定链路的全数字预编码方案已经不再适用。为了在多用户大规模MIMO系统中实现高频谱效率的同时降低硬件成本和功耗,使用非重叠子阵列架构以及重叠子阵列架构来进行混合预编码的设计。
首先设计模拟预编码矩阵FRF,由于各个天线子阵之间存在重叠的情况,观察公式(1)FRF的形式可以看出,当ΔM
(2)大阵列增益:等效信道应该充分收获阵列增益,这样它可以为每个数据流的传输提供尽可能大的增益。
上述优化问题可以描述为:
(7)
其中,,表示FRF中的非零元素满足的恒模限制条件。基于上述思想,设计模拟预编码矩阵非零元素为:
(8)
其中,FRF(s, t)表示FRF中的第(s, t)个元素。通过提取下行信道矩阵共轭转置部分元素的相位信息来设计模拟预编码FRF中的非零权值,从而实现与信道中的元素相位对齐,以此来获取大规模MIMO系统所提供的高阵列增益。其中,t=1,2,…,NtRF,对应s=1+(Nsub-△M)(t-1),…,Nsub+(Nsub-△M)(t-1),当t=1时,s=1,…,Nsub,当t=NRF时,s=1+(Nsub-△M)(NRF-1),…,NsubNRF-△M(NRF-1),FRF中的其他元素均为零。
在得到模拟预编码矩阵FRF后,进而可以得到射频等效信道矩阵Heq=HFRF。Heq是一个K×K维的低维度矩阵。此时,可以在数字基带针对低维度的射频等效信道矩阵Heq设计数字预编码矩阵。本算法采用ZF预编码算法进行数字预编码矩阵的设计,如下所示:
(9)
对数字预编码矩阵进行归一化处理以实现总发射功率的约束:
(10)
在得到模拟预编码矩阵FRF和数字预编码矩阵FBB后,即可根据公式(6)求得系统总的频谱效率。
4 仿真分析
在本节中,通过仿真结果来验证所提出的毫米波多用户大规模MIMO HB-PA算法的有效性。主要做了两组仿真,分别如下所示。
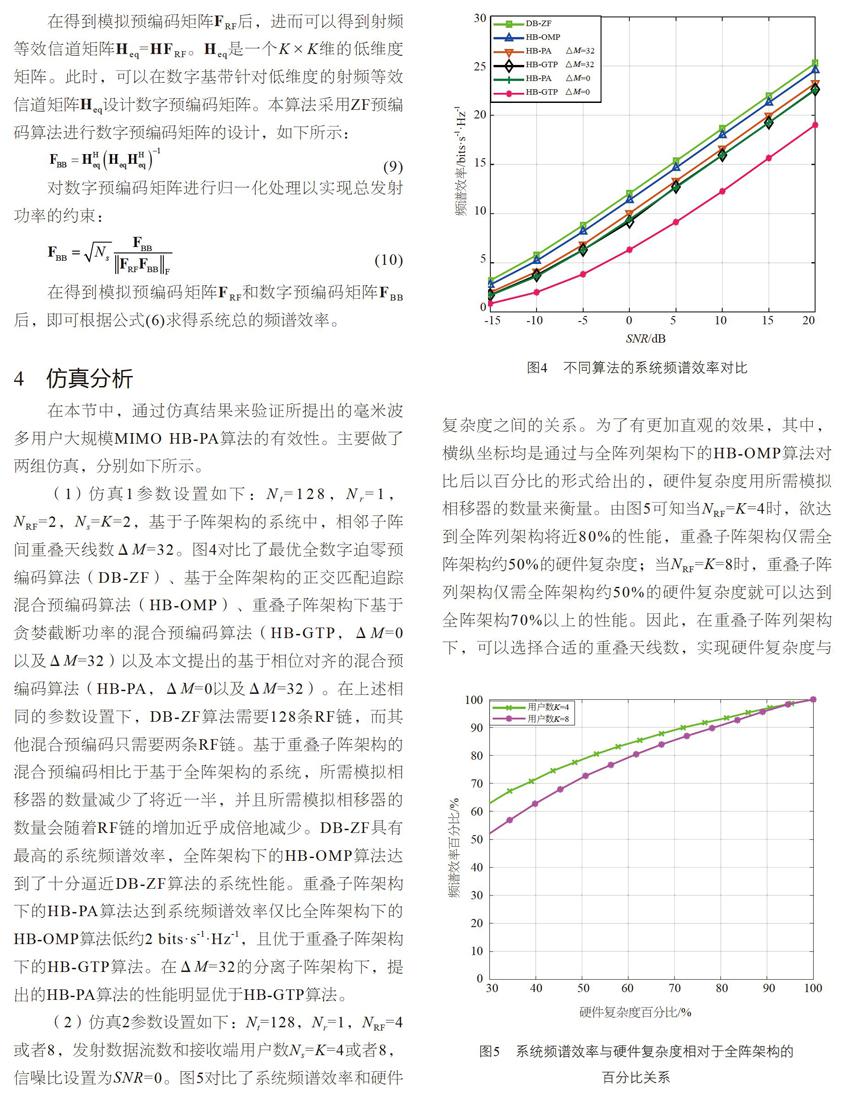
(1)仿真1参数设置如下:Nt=128,Nr=1,NRF=2,Ns=K=2,基于子阵架构的系统中,相邻子阵间重叠天线数ΔM=32。图4对比了最优全数字迫零预编码算法(DB-ZF)、基于全阵架构的正交匹配追踪混合预编码算法(HB-OMP)、重叠子阵架构下基于贪婪截断功率的混合预编码算法(HB-GTP,ΔM=0以及ΔM=32)以及本文提出的基于相位对齐的混合预编码算法(HB-PA,ΔM=0以及ΔM=32)。在上述相同的参数设置下,DB-ZF算法需要128条RF链,而其他混合预编码只需要两条RF链。基于重叠子阵架构的混合预编码相比于基于全阵架构的系统,所需模拟相移器的数量减少了将近一半,并且所需模拟相移器的数量会随着RF链的增加近乎成倍地减少。DB-ZF具有最高的系统频谱效率,全阵架构下的HB-OMP算法达到了十分逼近DB-ZF算法的系统性能。重叠子阵架构下的HB-PA算法达到系统频谱效率仅比全阵架构下的HB-OMP算法低约2 bits·s-1·Hz-1,且优于重叠子阵架构下的HB-GTP算法。在ΔM=32的分离子阵架构下,提出的HB-PA算法的性能明显优于HB-GTP算法。
(2)仿真2参数设置如下:Nt=128,Nr=1,NRF=4或者8,发射数据流数和接收端用户数Ns=K=4或者8,信噪比设置为SNR=0。图5对比了系统频谱效率和硬件复杂度之间的关系。为了有更加直观的效果,其中,横纵坐标均是通过与全阵列架构下的HB-OMP算法对比后以百分比的形式给出的,硬件复杂度用所需模拟相移器的数量来衡量。由图5可知当NRF=K=4时,欲达到全阵列架构将近80%的性能,重叠子阵架构仅需全阵架构约50%的硬件复杂度;当NRF=K=8时,重叠子阵列架构仅需全阵架构约50%的硬件复杂度就可以达到全阵架构70%以上的性能。因此,在重叠子阵列架构下,可以选择合适的重叠天线数,实现硬件复杂度与系统性能的很好折中。
5 结束语
文章提出了一种基于重叠子阵列架构的混合预编码HB-PA算法用于毫米波多用户大规模MIMO下行链路系统,并分析了非重叠子阵列架构和重叠子阵列架构的性能。HB-PA算法与传统全数字预编码、纯模拟预编码和现有混合预编码算法在不同信噪比下进行了实验,仿真结果表明,在相同的参数设置下HB-PA算法不仅能减少射频链的个数使硬件复杂度有效地降低,同时能够逼近全数字预编码的性能。
参考文献:
[1] F Boccardi, R W Heath, A Lozano, et al. Five disruptive technology directions for 5G[J]. IEEE Communications Magazine, 2014,52(2): 74-80.
[2] European Commission. Horizon 2020[EB/OL]. [2018-03-15]. https://ec.europa.eu/programmes/horizon2020/.
[3] E Hossain, M Hasan. 5g cellular: key enabling technologies and research challenges[J]. IEEE Instrumentation & Measurement Magazine, 2015,18(3): 11-21.
[4] 方箭,李景春,黃标,等. 5G频谱研究现状及展望[J]. 电信科学, 2015,31(12): 111-118.
[5] O E Ayach, S Rajagopal, S Abu-Surra, et al. Spatially Sparse Precoding in Millimeter Wave MIMO Systems[J]. IEEE Transactions on Wireless Communications, 2014(3): 1499-1513.
[6] Y Guo, L Li, X Wen, et al. Sub-array based hybrid precoding design for downlink millimeter-wave multi-user massive MIMO systems[C]//2017 9th International Conference on Wireless Communications and Signal Processing, 2017.
[7] Y Xing, Y Chen, L Yang. MMSE-based wideband hybrid precoding for massive MIMO systems[C]//2016 International Conference on Information and Communication Technology Convergence (ICTC), 2016.
[8] L Liang, W Xu, X Dong. Low-Complexity Hybrid Precoding in Massive Multiuser MIMO Systems[J]. IEEE Wireless Communications Letters, 2014,3(6): 653-656.
[9] L Dai, X Gao, J Quan, et al. Near-optimal hybrid analog and digital precoding for downlink mmWave massive MIMO systems[C]//2015 IEEE International Conference on Communications (ICC), 2015.
[10] N Song, T Yang, H Sun. Overlapped Sub-Array based Hybrid Beamforming for Millimeter Wave Multi-User Massive MIMO[J]. IEEE Signal Processing Letters, 2017,24(5): 550-554.
[11] F Sohrabi, W Yu. Hybrid digital and analog beamforming design for large-scale antenna arrays[J]. IEEE Journal of Selected Topics in Signal Processing, 2016,10(3): 501-513.



2017年12月3GPP完成了非独立组网(NSA)的5G新空口标准,同时计划在2018年6月完成独立组网(SA)的5G新空口标准,这将为5G商用铺平道路。传统的移动通信网的空口是一个以基站为中心的无线接入系统,而5G的空口将是以用户为中心的接入网,以接入云的形式强化了接入控制功能。另外,5G接入网将基带处理单元(BBU)的功能分解为分布单元(DU)和集中单元(CU),在原来的回传光传输系统基础上增加了前传和中传的环节。基站的大规模天线使得接入传输链路带宽可能达到100 Gb/s量级,而且传统的时分复用传输格式将会被基于低时延高效率的以太网技术取代。
——中国工程院院士邬贺铨
【摘 要】为了进一步解决MIMO系统中射频链路复杂度和系统性能相互制约的问题,重点研究了毫米波多用户大规模MIMO系统下行链路混合预编码设计方案,提出了一种基于相位对齐的重叠子阵列架构混合预编码算法(HB-PA算法)。该算法能够有效地减少射频链路的数量,同时频谱效率可以逼近全数字预编码的性能。通过仿真对比,该方案在硬件复杂度和系统性能等方面,比传统的典型混合预编码算法及基带数字预编码算法能够更有效地实现性能折中。
【关键词】混合预编码;重叠子阵列;毫米波;大规模MIMO
Phase Alignment Based Overlapped Sub-array Hybrid Precoding Algorithm for Millimeter-Wave Systems
XU Zhibin, GUO Yuehong, LI Lixin
(School of Electronics and Information, Northwestern Polytechnical University, Xi'an 710129, China)
[Abstract] In this paper, in order to solve the problem of restraint interacting between hardware complexity and system performance, the hybrid precoding architecture based on overlapped sub-array is studied. A hybrid precoding algorithm called HB-PA based on phase alignment with overlapped sub-array architecture is proposed. The proposed algorithm can effectively reduce the number of radio frequency links, while its spectral efficiency can approach the performance of full digital precoding. Simulation results demonstrate that, compared with the traditionally typical hybrid precoding and the baseband digital precoding algorithms, the proposed algorithm can more effective achieve the performance tradeoff between hardware complexity and system performance.
[Key words]hybrid precoding; overlapped sub-array; millimeter-wave; massive MIMO
1 引言
随着智能设备的不断增多以及新兴多媒体应用的不断出现,移动数据流量呈现出爆炸性增长。具备广域覆盖、高容量、低功耗和低时延等特点的5G技术目前受到了全世界的广泛关注[1]。一些主要国家及相关的行业委员会已经启动了5G项目。例如,美国的5G Americans、日本的ARIB Activities、中国的863-5G Promotion Group、韩国的5G论坛以及全球最大的欧盟研究和创新项目“地平线2020”计划[2]等为5G-PPP(The 5G Infrastructure Public Private Partnership,5G政府民间合作计划)提供资金,为无处不在的5G通信基础设施提供解决方案、架构、技术和标准。
5G的主要技术[3]包括大规模MIMO(Multiple-Input Multiple-Output,多輸入多输出)、HetNets(Heterogeneous Networks,异构网络)、mmWave(Millimeter-Wave,毫米波)通信、FD(Full Duplex,全双工)通信、C-RANS(Cloud-Radio Access Networks,云无线接入网络)、D2D(Device-to-Device,设备到设备)通信、新型多址接入技术、新型信道编码技术、能量感知通信以及能量收割技术等。作为关键技术之一的大规模MIMO技术,在基站或者用户端部署大量天线,根据天线波阵相干叠加原理,将发射功率集中在空间较小的区域,可以在发射机或接收机处实现多种性能增益,如复用增益、分集增益和天线增益。
无线数据通信近年来的显著增长推动了探讨无线电频谱中合适频带的研究。目前6 GHz以下微波频段的频谱资源日益紧缺,终将无法满足人们对更高数据传输速率的需求。毫米波是5G最重要的技术之一[4]。5G拟采用30 GHz~300 GHz的毫米波频段来为存在直达路径下的热点地区提供大容量覆盖和高速率支持。然而,在相同的传播环境下,毫米波容易受到氧气、水汽等的影响,导致传播损耗较大,同时降水、沙尘的负面影响也不可忽略。但是,由于毫米波的波长较小,毫米波元器件(比如天线)的尺寸相对于传统微波通信元器件要小得多,从而在相同的天线孔径总面积下可以部署更多数量的天线,实现大型天线阵列的集成,并且能够通过预编码技术来获得较大的天线阵列增益以补偿毫米波在极高频段下的严重路径损耗,从而改善传输质量。因此,毫米波与大规模MIMO技术的结合被视为5G最有前景的技术之一,而设计高效和稳健的预编码方案已成为当务之急。
在无线通信系统传输过程中,一般通过使用RF(Radio Frequency,射频)链路(其主要器件包括数模转换器、混频器和功率放大器等)对经过预处理的基带信号进行调制后再通过天线进行发射。然而,对于采用大型天线毫米波的系统而言,数字基带预编码是非常复杂和昂贵的,因为每个天线元件不仅需要专用的RF链路,还需要满足模拟前端射频电路的高动态范围。而模拟预编码方法虽然实现起来比较简单且成本较低,但是不够灵活,且波束导向精度相对较低。为了解决这些问题,文献[5]提出采用有限数量的RF链路预编码技术来实现硬件成本和系统性能的折中,从此混合预编码的概念被提出并迅速成为无线通信的一个研究热点。根据RF链路与发射天线之间的连接方式,在大规模MIMO混合预编码系统中有两种典型的系统架构:子阵列架构和全阵列架构。在全阵列架构中,阵列天线元连接到所有射频链上,而子阵列架构中的阵列天线元仅连接到某一特定射频链上[6]。
目前已有论文研究了基于全阵列架构的混合预编码算法。文献[5]在考虑毫米波信道空间稀疏特性的基础上,提出了一种正交匹配跟踪算法。文献[7]提出了一种基于MMSE(Minimum Mean-Square Error,最小均方误差)的混合预编码算法,并在拉格朗日算法的约束条件下得到了封闭解。文献[8]中提出的混合预编码方案在RF域中应用相位控制方法以获得有效信道矩阵,在基带处通过有效信道矩阵执行低维ZF(Zero-Forcing,破零)预编码。然而关于子阵列架构的预编码算法的研究相对较少。文献[9]中利用连续干扰消除来优化每个子阵列的容量。Song等人于2017年在文献[10]中首次提出了一种高效的混合预编码架构——重叠子阵列架构,即相邻子阵之间相互重叠,并采用一种重叠子阵架构下基于贪婪截断功率(Greedy Truncated Power,GTP)的多用户混合预编码算法。由于不同的混合预编碼架构具有各自的特点,因此,如何在不同混合预编码架构下设计硬件复杂度低、频谱效率高的混合预编码算法仍是目前混合预编码技术研究工作中需要攻克的难点。
本文针对上述问题,在毫米波多用户大规模MIMO下行链路系统中,提出了一种基于相位对齐(Phase Alignment,PA)的重叠子阵列架构混合预编码算法。首先通过提取下行链路信道矩阵共轭转置的部分相位信息来设计模拟预编码矩阵,从而实现信道元素的相位对齐,以获取大规模MIMO系统所提供的高阵列增益。在得到模拟预编码矩阵后,进而可以得到系统的射频等效信道矩阵,然后采用ZF算法求取数字预编码矩阵,最终实现混合波束形成方案的设计。与全阵列架构预编码方案相比,本文所提出的算法具有更高的频谱效率和更低的硬件实现复杂度。
2 系统模型
2.1 系统模型
毫米波多用户大规模MIMO混合预编码系统框图如图1所示。发射端将Ns个数据流发送到接收端Nt根天线上。发射端的数据流在基带上通过一个数字预编码器FBB处理后,再通过NRF个射频链路,最后经过一个模拟预编码器FRF,其中模拟预编码器一般通过模拟移相器实现。在全阵列架构中(如图2(a)所示),每个发射天线都连接到所有RF链路,这将导致很高的硬件实现复杂度以及成本开销。而在非重叠子阵列架构中(如图2(b)所示),每个发射天线仅连接到一个RF链路,连接在同一个RF链路的天线阵列称之为一个子阵列,且非重叠子阵列架构中所需模拟移相器的数量等于发射天线的数量。与全阵列架构相比,非重叠子阵列架构降低了模拟预编码过程中所需模拟移相器的数量和硬件实现复杂度,代价是部分频谱效率会有所降低。为了在系统性能和硬件实现复杂度之间做出折中,本文综合考虑了重叠子阵架构(如图2(c)所示)。所谓重叠子阵架构,就是相邻子阵之间存在重叠现象,基于该架构的混合波束形成系统在保持相对较低的复杂度的同时能够获得更高的阵列增益。
图2 三种不同类型的架构模型
在重叠子阵列架构中,每个基站存在NRF个子阵,假设每个子阵有相等的天线数Nsub,接收端为K个用户,相邻子阵重叠的天线数为ΔM。在图2(c)的例子中,RF链的个数为NRF=2,子阵的数量与RF链的数量相等,每个子阵的天线数量均为Nsub=4,而重叠天线数ΔM=2。当ΔM=0时,该重叠子阵架构转化为非重叠子阵架构,而当ΔM=Nsub时,该重叠子阵架构转化为全阵列架构。针对图1所示的多用户混合预编码系统,假设基站第K个子阵发送数据给第K个用户,则有Ns=NRF=K。由于用户均配置单天线,所以在接收端不需要对接收到的信号作进一步的合并处理,只需设计模拟预编码矩阵FRF和数字预编码矩阵FBB即可。其中,FBB仍可表示为FBB=[fBB1, fBB2, …, fBBK],而FRF表示为:
(1)
其中,是模拟预编码
矩阵FRF里面的非零权值,它们的模值满足。通过限制来标准化发射机的总发射功率,信道采用28 GHz的毫米波信道模型,为了充分利用大规模MIMO的特性,假设用户可以获取完美的信道状态信息。
2.2 信道模型
众所周知,与具有丰富散射体环境的低频信道不同,毫米波波段中的高路径损耗导致有限的空间选择性。为了体现毫米波信道稀疏散射体的特性,采用Saleh-Valenzuela信道模型来反映其散射特性[11]。毫米波信道模型如图3所示。假设用户k的信道具有L个散射体,则基站与用户k之间的信道矩阵可以表示为:
(2)
其中,gkl是用户k的第l路径的增益。Nr表示用户接收天线的个数。aHt(θkl)和ar(φkl)分别表示基站和用户终端的天线阵列响应矢量。为不失一般性,本文中使用ULA(Uniform Linear Array,均匀线性阵列)。θkl和φkl分别表示从发射机到用户k的第l路径的离开角和到达角,它们均遵循[0, 2π]的均匀分布。aHt(θkl)和ar(φkl)可以分别表示为:
(3)
(4)
其中,λ表示波长,d表示天线之间的距离,其中d=λ/2。
图3 毫米波信道模型
3 基于重叠子阵列的混合预编码设计
对于图1中的混合预编码的系统模型,用户k的接收信干噪比(SINR,Signal to Interference Plus Noise Ratio)被定義为SINRk,为高斯白噪声,SINRk可以表示为:
(5)
系统频谱效率用符号R表示,其表达式为:
(6)
在大规模MIMO系统中,每个天线需连接到特定链路的全数字预编码方案已经不再适用。为了在多用户大规模MIMO系统中实现高频谱效率的同时降低硬件成本和功耗,使用非重叠子阵列架构以及重叠子阵列架构来进行混合预编码的设计。
首先设计模拟预编码矩阵FRF,由于各个天线子阵之间存在重叠的情况,观察公式(1)FRF的形式可以看出,当ΔM
(2)大阵列增益:等效信道应该充分收获阵列增益,这样它可以为每个数据流的传输提供尽可能大的增益。
上述优化问题可以描述为:
(7)
其中,,表示FRF中的非零元素满足的恒模限制条件。基于上述思想,设计模拟预编码矩阵非零元素为:
(8)
其中,FRF(s, t)表示FRF中的第(s, t)个元素。通过提取下行信道矩阵共轭转置部分元素的相位信息来设计模拟预编码FRF中的非零权值,从而实现与信道中的元素相位对齐,以此来获取大规模MIMO系统所提供的高阵列增益。其中,t=1,2,…,NtRF,对应s=1+(Nsub-△M)(t-1),…,Nsub+(Nsub-△M)(t-1),当t=1时,s=1,…,Nsub,当t=NRF时,s=1+(Nsub-△M)(NRF-1),…,NsubNRF-△M(NRF-1),FRF中的其他元素均为零。
在得到模拟预编码矩阵FRF后,进而可以得到射频等效信道矩阵Heq=HFRF。Heq是一个K×K维的低维度矩阵。此时,可以在数字基带针对低维度的射频等效信道矩阵Heq设计数字预编码矩阵。本算法采用ZF预编码算法进行数字预编码矩阵的设计,如下所示:
(9)
对数字预编码矩阵进行归一化处理以实现总发射功率的约束:
(10)
在得到模拟预编码矩阵FRF和数字预编码矩阵FBB后,即可根据公式(6)求得系统总的频谱效率。
4 仿真分析
在本节中,通过仿真结果来验证所提出的毫米波多用户大规模MIMO HB-PA算法的有效性。主要做了两组仿真,分别如下所示。
(1)仿真1参数设置如下:Nt=128,Nr=1,NRF=2,Ns=K=2,基于子阵架构的系统中,相邻子阵间重叠天线数ΔM=32。图4对比了最优全数字迫零预编码算法(DB-ZF)、基于全阵架构的正交匹配追踪混合预编码算法(HB-OMP)、重叠子阵架构下基于贪婪截断功率的混合预编码算法(HB-GTP,ΔM=0以及ΔM=32)以及本文提出的基于相位对齐的混合预编码算法(HB-PA,ΔM=0以及ΔM=32)。在上述相同的参数设置下,DB-ZF算法需要128条RF链,而其他混合预编码只需要两条RF链。基于重叠子阵架构的混合预编码相比于基于全阵架构的系统,所需模拟相移器的数量减少了将近一半,并且所需模拟相移器的数量会随着RF链的增加近乎成倍地减少。DB-ZF具有最高的系统频谱效率,全阵架构下的HB-OMP算法达到了十分逼近DB-ZF算法的系统性能。重叠子阵架构下的HB-PA算法达到系统频谱效率仅比全阵架构下的HB-OMP算法低约2 bits·s-1·Hz-1,且优于重叠子阵架构下的HB-GTP算法。在ΔM=32的分离子阵架构下,提出的HB-PA算法的性能明显优于HB-GTP算法。
(2)仿真2参数设置如下:Nt=128,Nr=1,NRF=4或者8,发射数据流数和接收端用户数Ns=K=4或者8,信噪比设置为SNR=0。图5对比了系统频谱效率和硬件复杂度之间的关系。为了有更加直观的效果,其中,横纵坐标均是通过与全阵列架构下的HB-OMP算法对比后以百分比的形式给出的,硬件复杂度用所需模拟相移器的数量来衡量。由图5可知当NRF=K=4时,欲达到全阵列架构将近80%的性能,重叠子阵架构仅需全阵架构约50%的硬件复杂度;当NRF=K=8时,重叠子阵列架构仅需全阵架构约50%的硬件复杂度就可以达到全阵架构70%以上的性能。因此,在重叠子阵列架构下,可以选择合适的重叠天线数,实现硬件复杂度与系统性能的很好折中。
5 结束语
文章提出了一种基于重叠子阵列架构的混合预编码HB-PA算法用于毫米波多用户大规模MIMO下行链路系统,并分析了非重叠子阵列架构和重叠子阵列架构的性能。HB-PA算法与传统全数字预编码、纯模拟预编码和现有混合预编码算法在不同信噪比下进行了实验,仿真结果表明,在相同的参数设置下HB-PA算法不仅能减少射频链的个数使硬件复杂度有效地降低,同时能够逼近全数字预编码的性能。
参考文献:
[1] F Boccardi, R W Heath, A Lozano, et al. Five disruptive technology directions for 5G[J]. IEEE Communications Magazine, 2014,52(2): 74-80.
[2] European Commission. Horizon 2020[EB/OL]. [2018-03-15]. https://ec.europa.eu/programmes/horizon2020/.
[3] E Hossain, M Hasan. 5g cellular: key enabling technologies and research challenges[J]. IEEE Instrumentation & Measurement Magazine, 2015,18(3): 11-21.
[4] 方箭,李景春,黃标,等. 5G频谱研究现状及展望[J]. 电信科学, 2015,31(12): 111-118.
[5] O E Ayach, S Rajagopal, S Abu-Surra, et al. Spatially Sparse Precoding in Millimeter Wave MIMO Systems[J]. IEEE Transactions on Wireless Communications, 2014(3): 1499-1513.
[6] Y Guo, L Li, X Wen, et al. Sub-array based hybrid precoding design for downlink millimeter-wave multi-user massive MIMO systems[C]//2017 9th International Conference on Wireless Communications and Signal Processing, 2017.
[7] Y Xing, Y Chen, L Yang. MMSE-based wideband hybrid precoding for massive MIMO systems[C]//2016 International Conference on Information and Communication Technology Convergence (ICTC), 2016.
[8] L Liang, W Xu, X Dong. Low-Complexity Hybrid Precoding in Massive Multiuser MIMO Systems[J]. IEEE Wireless Communications Letters, 2014,3(6): 653-656.
[9] L Dai, X Gao, J Quan, et al. Near-optimal hybrid analog and digital precoding for downlink mmWave massive MIMO systems[C]//2015 IEEE International Conference on Communications (ICC), 2015.
[10] N Song, T Yang, H Sun. Overlapped Sub-Array based Hybrid Beamforming for Millimeter Wave Multi-User Massive MIMO[J]. IEEE Signal Processing Letters, 2017,24(5): 550-554.
[11] F Sohrabi, W Yu. Hybrid digital and analog beamforming design for large-scale antenna arrays[J]. IEEE Journal of Selected Topics in Signal Processing, 2016,10(3): 501-513.

