时变热环境下复合材料夹层板结构动力学响应分析
赵锐 于开平 崔乃刚

摘要: 复合材料结构已经在航空航天工程领域得到了广泛应用。当飞行器在大气中高速飞行时,气动热载荷会改变复合材料结构的动力学特性和动力学响应。目前,学者对恒定热环境下复合材料结构动力学响应的数值仿真进行了较多研究,而对于时变热环境下的数值仿真还尚未开展研究。提出了一种用于时变温度环境下复合材料夹层板结构动力学响应计算的数值仿真分析方法。首先,利用基于分段剪切变形理论的板单元建立了考虑热环境影响的复合材料夹层板结构有限元模型。然后,利用时变结构时间有限元方法计算了时变温度环境下复合材料夹层板结构的动力学响应。最后,对动态响应进行时频分析,并与由理论模态分析方法计算出的固有频率参考值进行对比,验证了该方法的有效性与精确性。提出的数值仿真分析方法可以有效地预示时变热环境下复合材料夹层板结构的热振响应,为热环境下复合材料结构的设计与分析提供了理论基础。
关键词: 结构振动; 复合材料结构; 热振分析; 时变结构; 时程积分算法
中图分类号: O327; V214.8 文献标志码:A文章编号1004-4523(2018)02-0329-07
DOI:10.16385/j.cnki.issn.1004-4523.2018.02.017
引言
复合材料结构由于具有高比刚度、高比强度等优良的性能,已经在航空航天、车辆、土木等工程领域得到了广泛应用。比如,高超声速飞行器的热防护结构通常采用的就是复合材料夹层板结构,而高超声速飞行器在大气中高速飞行时该结构会受到严酷的气动热载荷和气动力载荷的作用。在这种情况下,气动力载荷会引起复合材料板结构的振动,而热载荷会引起热弹性应力并且改变材料的力学性能,这些因素会进一步影响这些结构的振动特性和振动响应,进而会影响飞行器的性能甚至可能会导致飞行任务失败。因此,精确地预示热环境下复合材料板结构的振动特性和振动响应是非常重要的。
目前,已经有许多学者运用解析方法研究了热环境下复合材料层合板和夹层板结构的振动问题。Huang等[1]利用高阶剪切变形模型研究了湿热环境下复合材料层合板的非线性振动和动力学响应。Girish和Ramachandra[2]利用高阶剪切变形模型研究了均匀热环境下对称复合材料层合板的后屈曲振动问题。Matsunaga[3]提出了一个用于热环境下角铺设复合材料层合板和三明治板自由振动和稳定性分析的全局高阶变形模型。Li等[4]利用高阶剪切变形模型和von Karman非线性应变-位移关系执行了热环境下正交铺设复合材料层合圆柱壳的大幅振动分析。Chen等[5]利用一阶剪切变形模型研究了热环境下具有温变材料属性的预应力复合材料层合板的振动行为。Fazzolari和Carrera[6]提出了分层三角里兹公式,并利用该公式研究了热环境下具有复合材料层合面板的夹层板的自由振动。他们[7]还利用该公式研究了预屈曲和后屈曲的各向异性复合材料层合板的自由振动响应。Liu和Li[8]采用一个等效非经典模型研究了受到集中简谐激励力和热载荷的由两种各向同性材料组成的矩形夹层板的振动和声学响应。Kim等[9]利用一阶剪切变形模型研究了受到电磁场和热场载荷作用的复合材料层合板的振动和稳定性问题。Li等[10]利用一阶剪切变形模型研究了热环境下非对称矩形复合材料层合板的振动和声辐射响应。Li等[11-12]利用分段剪切变形模型研究了热环境下复合材料层合板和夹层板的振动和声学响应特性。Du等[13]利用一阶剪切变形模型和von Karman非线性应变-位移关系研究了沿厚度方向具有温度梯度的复合材料层合板的振动和声学响应。
此外,还有许多学者运用数值方法研究了热环境下复合材料层合板和夹层板结构的振动问题。Oh等[14]利用分层模型建立了受到热压电载荷的压电复合材料层合板振动分析的非线性有限元方程。Makhecha等[15]以高阶zigzag模型为基础发展了一种用于热/机械载荷作用下厚复合材料层合板动力学分析的C0连续8节点四边形板单元。Ganapathi等[16]利用上述单元对热/机械载荷作用下的厚复合材料层合板和夹层板进行了非线性动力学分析。Parhi等[17]以一阶剪切变形模型为基础提出了一种用于湿热环境下多分层双曲壳动力学分析的二次等参单元。Patel等[18]以高阶zigzag模型为基础发展了一种用于湿热环境下厚复合材料层合板静力学和动力学分析的C0连续8节点四边形板单元。Tawfik等[19]利用基于von Karman非线性应变-位移关系的非线性有限元模型研究了受到气动力和热载荷的嵌入形状記忆合金的各向同性板的热屈曲和气弹行为。Hong和Jane[20]采用广义微分求积方法研究了受到正弦变化时变温度载荷的正交铺设复合材料层合板的层间应力和变形。Oh和Cho[21]以高阶zigzag模型为基础发展了一种用于更加精确预示复合材料层合板热-电-机耦合行为的3节点三角形单元,其中位移场和温度场均是由全局三次光滑场和线性zigzag场叠加而成的。Park等[22]利用一阶剪切变形模型建立了受到热载荷的嵌入形状记忆合金的复合材料层合板振动分析的非线性有限元方程,并且研究了板在预屈曲和后屈曲状态下的振动特性。Rao和Sinha[23]发展了一种用于研究湿度和温度对多向复合材料板振动响应影响的20节点六面体等参单元。Shiau和Kuo[24]发展了一种用于热屈曲夹层板自由振动分析的每个节点具有24个自由度的3节点三角形板单元。Singha等[25]采用基于一阶剪切变形模型的4节点四边形研究了热环境下复合材料斜板的小幅振动特性。Vangipuram和Ganesan[26]利用有限元方法研究了热环境下具有温变材料属性黏弹性芯层的矩形复合材料黏弹性夹层板的自由振动和阻尼特性。Pradeep和Ganesan[27]研究了多层矩形黏弹性夹层板的热屈曲和振动特性。Jeyaraj等[28-29]利用基于经典层合板模型的4节点四边形板单元研究了温度对受到简谐激励力的复合材料层合板和多层黏弹性夹层板的振动和声学响应特性的影响。Rath和Sahu[30]采用基于一阶剪切变形模型的8节点四边形等参板单元执行了湿热环境下编织纤维复合材料层合板的自由振动分析。Ibrahim等[31]利用一阶剪切变形模型和von Karman非线性应变-位移关系建立了用于受到热载荷和气动载荷的混合形状记忆合金的复合材料层合板的非线性颤振分析的非线性有限元模型。Shariyat[32]提出了一个用于受到热-机载荷的夹层板的静力学和动力学分析的全局-局部高阶剪切变形模型,并且基于该模型发展出了一个C1连续的Hermitian矩形板单元。Panda等[33]利用基于一阶剪切变形模型的8节点四边形等参板单元研究了受到温湿载荷的分层复合材料层合板的自由振动问题。Natarajan等[34]利用一阶剪切变形模型和扩展有限元方法研究了水分浓度和温度梯度对复合材料层合板自由振动和屈曲特性的影响。Zhang等[35]运用实验和数值方法研究了受到四边自由边界条件和极端热载荷的具有陶瓷泡沫芯层的纤维增强莫来石夹层板的振动特性。Katariya和Panda[36]采用基于高阶剪切变形模型的每个节点具有10个自由度的9节点等参Lagrangian单元研究了复合材料双曲壳的热屈曲和振动行为。Zhao等[37]提出了复合材料板结构分段剪切变形模型,并以该模型为基础构建了一种用于复合材料板结构热振分析的4节点四边形等参板单元。与现有的分层模型、zigzag模型和等效单层模型相比,分段剪切变形模型可以用较小的计算量获得足够精确的计算结果。
第2期赵锐,等: 时变热环境下复合材料夹层板结构动力学响应分析振 动 工 程 学 报第31卷在上述关于热环境下复合材料板结构振动分析的研究工作中,热环境均被假设为不随时间变化的恒定温度场,此时的复合材料板结构是时不变结构。然而,当高超声速飞行器在大气中高速飞行时,气动热载荷是随时间变化的,结构内的温度场也是随时间变化的,此时的复合材料板结构是时变结构。针对这种情况,本文提出了一种用于时变温度环境下复合材料夹层板结构动力学响应计算的数值仿真分析方法。首先,利用基于分段剪切变形理论的板单元建立了考虑热环境影响的复合材料夹层板结构有限元模型。然后,利用时变结构时间有限元方法计算了时变温度环境下复合材料夹层板结构的动力学响应。最后,对动态响应进行时频分析,并与由理论模态分析方法计算出的固有频率参考值进行对比,验证了本文提出的方法的有效性与精确性。
1热环境下复合材料夹层板结构有限元模型〖*2〗1.1分段剪切变形模型在分段剪切变形模型[37]中,复合材料层合板/夹层板沿着厚度方向被划分为若干段,其中每一段既可以是单层正交各向异性材料也可以是多层层合复合材料。在本研究中,复合材料夹层板结构沿厚度方向划分的段数为3段,如图1所示。
图1复合材料夹层板分段运动的一维表示
Fig.1One dimensional representation of piecewise kinematics of composite sandwich plates
在分段剪切变形模型[37]中,假设层合板内的横向位移沿着厚度方向是不变的,假设每一段的横截面在变形后依旧保持为平面,假设相邻段界面处的位移是连续的,则复合材料层合板结构第1,2,3段的位移场可以表达为:u1=u0+zbiψx2+z-zbiψx1
v1=v0+zbiψy2+z-zbiψy1
w1=w0 (1)
u2=u0+zψx2
v2=v0+zψy2
w2=w0(2)
u3=u0+ztiψx2+z-ztiψx3
v3=v0+ztiψy2+z-ztiψy3
w3=w0(3)式中u0,v0,w0分别表示位于层合板中面上的点沿着x,y,z轴方向的位移;uj,vj,wj分别表示位于层合板第j段(j=1,2,3)上的点沿着x,y,z轴方向的位移;Ψxj,Ψyj分别表示层合板第j段(j=1,2,3)横截面法线绕着y轴和x轴的转角。
1.2系统运动控制方程
利用基于分段剪切變形模型的4节点四边形层合板单元(PSDT-Quad4单元)[37]可以建立起热环境下复合材料夹层板结构的有限元模型。由该有限元模型得到的热环境下复合材料板结构运动控制方程,包括静态变形运动控制方程(即静力学方程)和相对于静平衡位置的动态变形运动控制方程(即动力学方程)[37]:K0qs=FΔT+Fs(4)
Md+Cd+K0+Kσqd=Fd(5)式中M,C,K0分别表示复合材料夹层板结构的质量、阻尼和刚度矩阵;Fs和Fd分别表示静态和动态机械外力向量;F△T表示热载荷等效节点力向量;Kσ表示由预应力引起的几何刚度矩阵;qs和qd分别表示结构的静态和动态变形。由方程(5)可以看出,由机械和热载荷引起的预应力将改变复合材料层合板结构的刚度属性,进而将影响层合板结构的固有频率、振型和其他动力学特性。
上述有限元方程不仅可以用于稳态均匀热环境下复合材料板结构的振动分析,还可以用于瞬态均匀热环境下复合材料板结构的振动分析。如果结构温度场T是随时间变化的,那么复合材料夹层板结构的几何刚度矩阵Kσ也将随着时间变化,即Kσ=Kσ(t)。此外,如果材料的弹性模量是随温度变化的,那么复合材料板结构的刚度矩阵K0也将随时间变化,即K0=K0(t)。也就是说,在瞬态热环境下,复合材料板结构运动控制方程中的刚度矩阵将变为关于时间的函数,所以瞬态热环境下的复合材料板结构属于线性时变结构。因此,瞬态热环境下复合材料板结构的振动问题属于线性时变结构动力学问题,建立的系统动力学方程是时变系统常微分方程。首先,针对不同时刻的温度载荷对静力学方程进行求解可以计算出这些时刻的静态变形,然后由这些静态变形可以进一步计算出预应力以及对应的几何刚度矩阵,最后可以利用线性时变结构动响应数值算法对动力学方程进行数值求解。
2线性时变结构时间有限元算法
线性时变结构动力学方程的一般表达式为Mtt+Ctt+Ktqt=Ft(6)在一个典型的时间单元[tk-1,tk]内,利用Galerkin方法,广义坐标q、广义速度v、广义力F、广义系统矩阵M,C,K可以分别近似为:q=ΦT×, =T×, v=ΨT×,
=T×, M=LTM×, C=LTC×,
K=LTK×, F=NT×(7)式中“×”表示复合矩阵乘法[38,40];Φ,Ψ,N,LM, LC,LK分别为用于近似变量q,v,F,M,C,K的插值基函数。
由文献[38]可知,线性时变结构不协调时间有限元算法(TFEM算法)的递推公式为D11×D12×
D21×DM22×+DC22×=
g1
g2+0
DFI(8)式中,“”表示克罗内克积,I表示单位矩阵,且有:D11=∫tktk-1ΦTLTM+ΨΦTTMdt-
ΨΦTLTMtk(9)
D12=∫tktk-1ΨΨTLTMdt(10)
D21=-∫tktk-1ΦΦTLTKdt(11)
DM22=∫tktk-1ΨTLTM+ΦΨTTMdt-
ΦΨTLTMtk(12)
DC22=-∫tktk-1ΦΨTLTCdt(13)
DF=-∫tktk-1ΦNTdt(14)3时变温度环境下复合材料夹层板结构瞬态响应分析在本节中,将联合使用分段剪切变形板单元和不协调时间有限元算法对瞬态均匀热环境下复合材料板结构的动力学问题进行数值仿真。本算例的研究对象为受到四边简支边界条件和均匀热载荷的具有正交各向异性面板和各向同性芯层的矩形夹层板。复合材料夹层板结构的几何尺寸为0.4 m×0.3 m×0.01 m,其中面板和芯层的厚度分别为0.5 mm和9 mm。面板的材料属性如下:Ef1=132 GPa, Ef2=10.3 GPa,
Gf12=Gf13=6.5 GPa, Gf23=3.91 GPa,
νf12=0.25, ρf=1570 kg/m3,
αf1=1.2×10-6/℃, αf2=2.4×10-5/℃芯层的材料属性如下:Ec=10 MPa, νc=0.3, ρc=40 kg/m3,
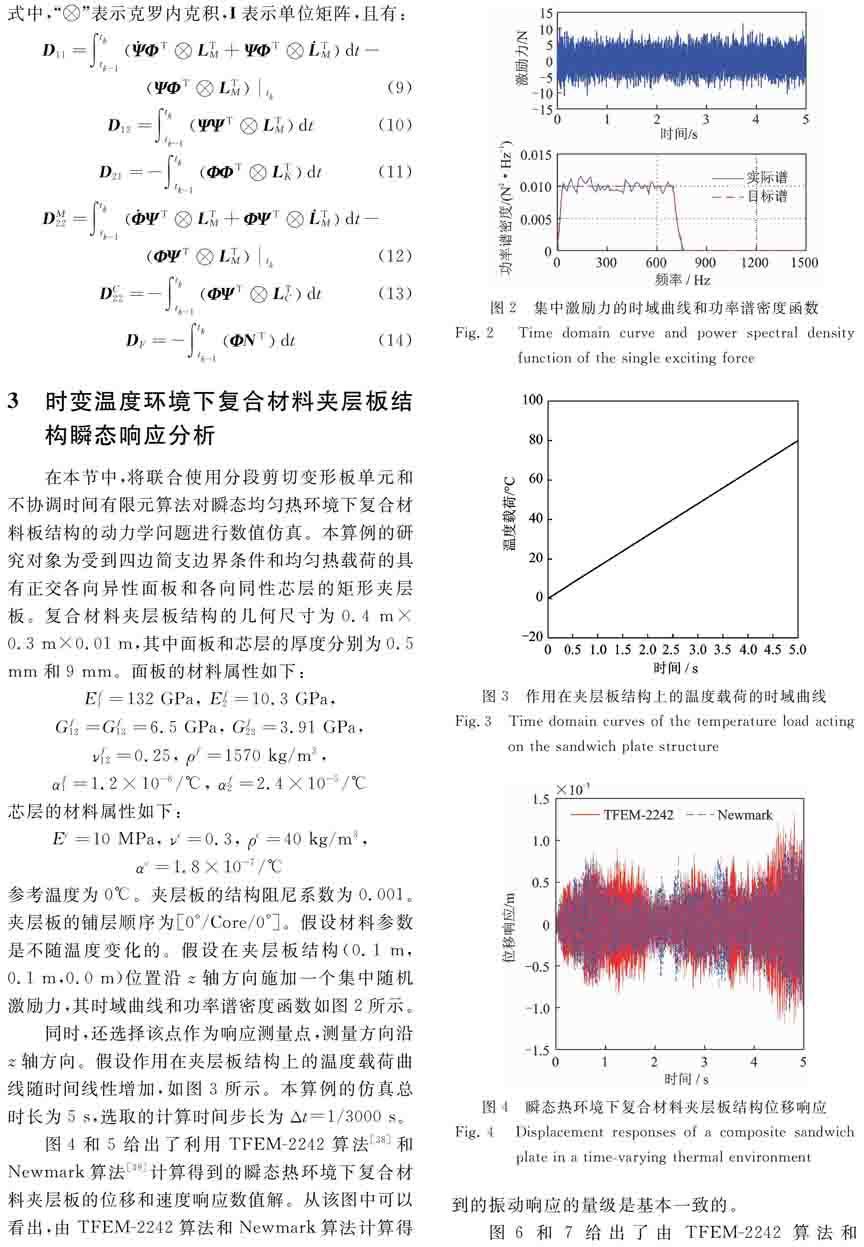
αc=1.8×10-7/℃參考温度为0℃。夹层板的结构阻尼系数为0.001。夹层板的铺层顺序为[0°/Core/0°]。假设材料参数是不随温度变化的。假设在夹层板结构(0.1 m,0.1 m,0.0 m)位置沿z轴方向施加一个集中随机激励力,其时域曲线和功率谱密度函数如图2所示。
图2集中激励力的时域曲线和功率谱密度函数
Fig.2Time domain curve and power spectral density function of the single exciting force图3作用在夹层板结构上的温度载荷的时域曲线
Fig.3Time domain curves of the temperature load acting on the sandwich plate structure同时,还选择该点作为响应测量点,测量方向沿z轴方向。假设作用在夹层板结构上的温度载荷曲线随时间线性增加,如图3所示。本算例的仿真总时长为5 s,选取的计算时间步长为Δt=1/3000 s。
图4瞬态热环境下复合材料夹层板结构位移响应
Fig.4Displacement responses of a composite sandwich plate in a time-varying thermal environment
图5瞬态热环境下复合材料夹层板结构速度响应
Fig.5Velocity responses of a composite sandwich plate in a time-varying thermal environment图4和5给出了利用TFEM-2242算法[38]和Newmark算法[39]计算得到的瞬态热环境下复合材料夹层板的位移和速度响应数值解。从该图中可以看出,由TFEM-2242算法和Newmark算法计算得到的振动响应的量级是基本一致的。
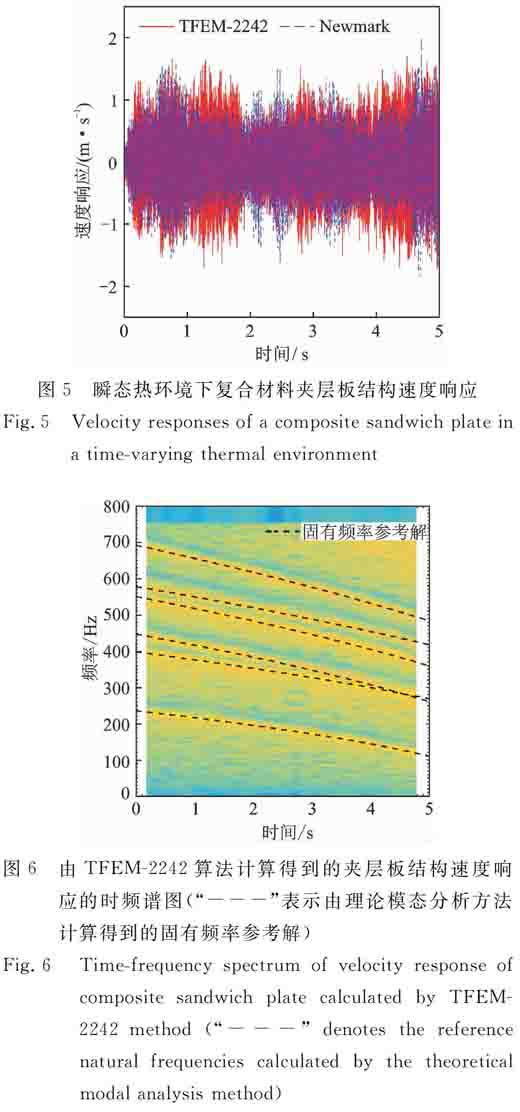
图6由TFEM-2242算法计算得到的夹层板结构速度响应的时频谱图(“---”表示由理论模态分析方法计算得到的固有频率参考解)
Fig.6Time-frequency spectrum of velocity response of composite sandwich plate calculated by TFEM-2242 method (“---” denotes the reference natural frequencies calculated by the theoretical modal analysis method)
图7由Newmark算法计算得到的夹层板结构速度响应的时频谱图(“---”表示由理论模态分析方法计算得到的固有频率参考解)
Fig.7Time-frequency spectrum of velocity response of composite sandwich plate calculated by Newmark method (“---” denotes the reference natural frequencies calculated by the theoretical modal analysis method)
图6和7给出了由TFEM-2242算法和Newmark算法计算得到的速度响应数值解的时频谱图,并且将由理论模态分析方法计算得到的系统各阶固有频率作为参考解。从该图中可以看出,TFEM-2242算法的数值解的频率信息与参考解吻合较好,该数值解能够准确地反映出系统固有频率随时间的变化情况,而Newmark算法的数值解的频率信息与参考解之间差异较大,这是因为Newmark算法具有显著的频散特性,进而导致了从数值解中辨识出的系统各阶固有频率明显偏小。
4结论
本文提出了一种用于时变温度环境下复合材料夹层板结构动力学响应计算的数值仿真分析方法。首先,利用基于分段剪切变形模型的板单元(PSDT-Quad4单元)建立考虑热环境影响的复合材料夹层板结构有限元模型。然后,利用线性时变结构不协调时间有限元算法(TFEM-2242算法)计算时变温度环境下复合材料夹层板结构的动力学响应。最后,对动响应进行时频分析,并与由理论模态分析方法计算得到的固有频率参考值进行对比,验证了本文提出的方法的有效性与精确性。
数值结果表明,TFEM-2242算法数值解的频率信息与参考解吻合较好,数值解能够准确地反映出系统固有频率随时间的变化情况,而Newmark算法数值解的频率信息与参考解之间差异较大。TFEM-2242算法适用于瞬态热环境下复合材料板结构的瞬态响应分析问题,并且其计算精度高于Newmark算法。
本文提出的数值仿真分析方法可以有效地预示时变热环境下复合材料夹层板结构的热振响应,为热环境下复合材料夹层板结构的设计与分析提供了理论基础。
參考文献:
[1]Huang X L, Shen H S, Zheng J J. Nonlinear vibration and dynamic response of shear deformable laminated plates in hygrothermal environments [J]. Composites Science and Technology,2004, 64(10-11):1419—1435.
[2]Girish J, Ramachandra L S. Thermal postbuckled vibrations of symmetrically laminated composite plates with initial geometric imperfections [J]. Journal of Sound and Vibration, 2005, 282(3-5):1137—1153.
[3]Matsunaga H. Free vibration and stability of angle-ply laminated composite and sandwich plates under thermal loading [J]. Composite Structures, 2007, 77(2):249—262.
[4]Li Z, Chen X, Yu H. Large-amplitude vibration analysis of shear deformable laminated composite cylindrical shells with initial imperfections in thermal environments [J]. Journal of Engineering Mechanics, 2012, 140(3):552—565.
[5]Chen C S, Chen C W, Chen W R, et al. Thermally induced vibration and stability of laminated composite plates with temperature-dependent properties [J]. Meccanica, 2013, 48(9):2311—2323.
[6]Fazzolari F A, Carrera E. Free vibration analysis of sandwich plates with anisotropic face sheets in thermal environment by using the hierarchical trigonometric Ritz formulation [J]. Composites Part B: Engineering, 2013, 50:67—81.
[7]Fazzolari F A, Carrera E. Accurate free vibration analysis of thermo-mechanically pre/post-buckled anisotropic multilayered plates based on a refined hierarchical trigonometric Ritz formulation [J]. Composite Structures, 2013, 95:381—402.
[8]Liu Y, Li Y. Vibration and acoustic response of rectangular sandwich plate under thermal environment [J]. Shock and Vibration, 2013, 20(5):1011—1030.
[9]Kim S K, Choi J, Park S, et al. Vibration and stability of laminated composite plates subjected to a combined electromagnetic and thermal field [J]. Journal of Vibration and Control, 2015, 21(12):2325—2339.
[10]Li W, Li Y. Vibration and sound radiation of an asymmetric laminated plate in thermal environments [J]. Acta Mechanica Solida Sinica, 2015, 28(1):11—22.
[11]Li X, Yu K, Han J, et al. A piecewise shear deformation theory for free vibration of composite and sandwich panels [J]. Composite Structures, 2015, 124:111—119.
[12]Li X, Yu K. Vibration and acoustic responses of composite and sandwich panels under thermal environment [J]. Composite Structures, 2015, 131:1040—1049.
[13]Du M, Geng Q, Li Y. Vibrational and acoustic responses of a laminated plate with temperature gradient along the thickness [J]. Composite Structures, 2016, 157:483—493.
[14]Oh I K, Han J H, Lee I. Postbuckling and vibration characteristics of piezolaminated composite plate subject to thermo-piezoelectric loads [J]. Journal of Sound and Vibration, 2000, 233(1):19—40.
[15]Makhecha D P, Ganapathi M, Patel B P. Dynamic analysis of laminated composite plates subjected to thermal/mechanical loads using an accurate theory [J]. Composite Structures, 2001, 51(3):221—236.
[16]Ganapathi M, Patel B P, Makhecha D P. Nonlinear dynamic analysis of thick composite/sandwich laminates using an accurate higher-order theory [J]. Composites Part B: Engineering, 2004, 35(4):345—355.
[17]Parhi P K, Bhattacharyya S K, Sinha P K. Hygrothermal effects on the dynamic behavior of multiple delaminated composite plates and shells [J]. Journal of Sound and Vibration, 2001, 248(2):195—214.
[18]Patel B P, Ganapathi M, Makhecha D P. Hygrothermal effects on the structural behaviour of thick composite laminates using higher-order theory [J]. Composite Structures, 2002, 56(1):25—34.
[19]Tawfik M, Ro J J, Mei C. Thermal post-buckling and aeroelastic behaviour of shape memory alloy reinforced plates [J]. Smart Materials and Structures, 2002, 11(2):297—307.
[20]Hong C C, Jane K C. Shear deformation in thermal vibration analysis of laminated plates by the GDQ method [J]. International Journal of Mechanical Sciences, 2003, 45(1):21—36.
[21]Oh J, Cho M. A finite element based on cubic zig-zag plate theory for the prediction of thermo-electric-mechanical behaviors [J]. International Journal of Solids and Structures, 2004, 41(5):1357—1375.
[22]Park J S, Kim J H, Moon S H. Vibration of thermally post-buckled composite plates embedded with shape memory alloy fibers [J]. Composite Structures, 2004, 63(2):179—188.
[23]Rao V V S, Sinha P K. Dynamic response of multidirectional composites in hygrothermal environments [J]. Composite Structures, 2004, 64(3):329—338.
[24]Shiau L C, Kuo S Y. Free vibration of thermally buckled composite sandwich plates [J]. Journal of Vibration and Acoustics, 2006, 128(1):1—7.
[25]Singha M K, Ramachandra L S, Bandyopadhyay J N. Vibration behavior of thermally stressed composite skew plate [J]. Journal of Sound and Vibration, 2006, 296(4-5):1093—1102.
[26]Vangipuram P, Ganesan N. Buckling and vibration of rectangular composite viscoelastic sandwich plates under thermal loads [J]. Composite Structures, 2007, 77(4):419—429.
[27]Pradeep V, Ganesan N. Thermal buckling and vibration behavior of multi-layer rectangular viscoelastic sandwich plates [J]. Journal of Sound and Vibration, 2008, 310(1-2):169—183.
[28]Jeyaraj P, Ganesan N, Padmanabhan C. Vibration and acoustic response of a composite plate with inherent material damping in a thermal environment [J]. Journal of Sound and Vibration, 2009, 320(1-2):322—338.
[29]Jeyaraj P, Padmanabhan C, Ganesan N. Vibro-acoustic behavior of a multilayered viscoelastic sandwich plate under a thermal environment [J]. Journal of Sandwich Structures and Materials, 2011, 13(5):509—537.
[30]Rath M, Sahu S. Vibration of woven fiber laminated composite plates in hygrothermal environment [J]. Journal of Vibration and Control, 2012, 18(13):1957—1970.
[31]Ibrahim H H, Tawfik M, Negm H M. Thermal buckling and nonlinear flutter behavior of shape memory alloy hybrid composite plates [J]. Journal of Vibration and Control, 2011, 17(3):321—333.
[32]Shariyat M. A generalized global-local high-order theory for bending and vibration analyses of sandwich plates subjected to thermo-mechanical loads [J]. International Journal of Mechanical Sciences, 2010, 52(3):495—514.
[33]Panda H S, Sahu S K, Parhi P K. Hygrothermal effects on free vibration of delaminated woven fiber composite plates - Numerical and experimental results [J]. Composite Structures, 2013, 96:502—513.
[34]Natarajan S, Deogekar P S, Manickam G, et al. Hygrothermal effects on the free vibration and buckling of laminated composites with cutouts [J]. Composite Structures, 2014, 108:848—855.
[35]Zhang X, Yu K, Bai Y, et al. Thermal vibration characteristics of fiber-reinforced mullite sandwich structure with ceramic foams core [J]. Composite Structures, 2015, 131:99—106.
[36]Katariya P V, Panda S K. Thermal buckling and vibration analysis of laminated composite curved shell panel [J]. Aircraft Engineering and Aerospace Technology, 2016, 88(1):97—107.
[37]Zhao R, Yu K, Hulbert G M, et al. Piecewise shear deformation theory and finite element formulation for vibration analysis of laminated composite and sandwich plates in thermal environments [J]. Composite Structures, 2017, 160:1060—1083.
[38]Zhao R, Yu K, Hulbert G M. Time discontinuous finite element method for transient response analysis of linear time-varying structures [J]. Meccanica, 2018,53(4-5):703—726.
[39]Zhao R, Yu K. An efficient transient analysis method for linear time-varying structures based on multi-level substructuring method [J]. Computers & Structures, 2015, 146:76—90.
[40]Zhao R, Yu K. Hamilton′s law of variable mass system and time finite element formulations for time-varying structures based on the law [J]. International Journal for Numerical Methods in Engineering, 2014, 99(10):711—736.
Vibration response analysis of a composite sandwich plate under a
time-varying thermal environmentZHAO Rui1 , YU Kai-ping1 , CUI Nai-gang2 (1. Department of Astronautic Science and Mechanics, Harbin Institute of Technology, Harbin 150001, China;
2. Department of Astronautic Engineering, Harbin Institute of Technology, Harbin 150001, China)
Abstract: The composite structure has been widely used in the aerospace engineering. When the aircraft is flying at high speed in the atmosphere, the aerodynamic heat load will change the dynamic characteristic and dynamic response of the composite structure. At present, the numerical simulation of the dynamic response of composite structures in constant temperature environment has been studied by scholars, while the numerical simulation in the time-varying temperature environment has not been studied yet. In this paper, a numerical simulation analysis method for the dynamic response analysis of composite sandwich plates in time-varying temperature environments is proposed. Firstly, the finite element model of composite sandwich plates is established utilizing the plate element based on the piecewise shear deformation theory. And then the dynamic response of composite sandwich plates under the time-varying temperature environment is calculated by using the time finite element method for time-varying structures. Finally, the time-frequency analysis of the dynamic response is performed and the results are compared with the reference natural frequencies obtained using the theoretical modal analysis, by which the validity and accuracy of the proposed method are verified. The numerical simulation analysis method proposed in this paper can effectively predict the thermal vibration response of composite sandwich plates in time-varying temperature environments, and provides a theoretical basis for the design and analysis of composite structures in thermal environment.
Key words: structural vibration; composite structure; thermal vibration analysis; time-varying structure; time integration algorithm



摘要: 复合材料结构已经在航空航天工程领域得到了广泛应用。当飞行器在大气中高速飞行时,气动热载荷会改变复合材料结构的动力学特性和动力学响应。目前,学者对恒定热环境下复合材料结构动力学响应的数值仿真进行了较多研究,而对于时变热环境下的数值仿真还尚未开展研究。提出了一种用于时变温度环境下复合材料夹层板结构动力学响应计算的数值仿真分析方法。首先,利用基于分段剪切变形理论的板单元建立了考虑热环境影响的复合材料夹层板结构有限元模型。然后,利用时变结构时间有限元方法计算了时变温度环境下复合材料夹层板结构的动力学响应。最后,对动态响应进行时频分析,并与由理论模态分析方法计算出的固有频率参考值进行对比,验证了该方法的有效性与精确性。提出的数值仿真分析方法可以有效地预示时变热环境下复合材料夹层板结构的热振响应,为热环境下复合材料结构的设计与分析提供了理论基础。
关键词: 结构振动; 复合材料结构; 热振分析; 时变结构; 时程积分算法
中图分类号: O327; V214.8 文献标志码:A文章编号1004-4523(2018)02-0329-07
DOI:10.16385/j.cnki.issn.1004-4523.2018.02.017
引言
复合材料结构由于具有高比刚度、高比强度等优良的性能,已经在航空航天、车辆、土木等工程领域得到了广泛应用。比如,高超声速飞行器的热防护结构通常采用的就是复合材料夹层板结构,而高超声速飞行器在大气中高速飞行时该结构会受到严酷的气动热载荷和气动力载荷的作用。在这种情况下,气动力载荷会引起复合材料板结构的振动,而热载荷会引起热弹性应力并且改变材料的力学性能,这些因素会进一步影响这些结构的振动特性和振动响应,进而会影响飞行器的性能甚至可能会导致飞行任务失败。因此,精确地预示热环境下复合材料板结构的振动特性和振动响应是非常重要的。
目前,已经有许多学者运用解析方法研究了热环境下复合材料层合板和夹层板结构的振动问题。Huang等[1]利用高阶剪切变形模型研究了湿热环境下复合材料层合板的非线性振动和动力学响应。Girish和Ramachandra[2]利用高阶剪切变形模型研究了均匀热环境下对称复合材料层合板的后屈曲振动问题。Matsunaga[3]提出了一个用于热环境下角铺设复合材料层合板和三明治板自由振动和稳定性分析的全局高阶变形模型。Li等[4]利用高阶剪切变形模型和von Karman非线性应变-位移关系执行了热环境下正交铺设复合材料层合圆柱壳的大幅振动分析。Chen等[5]利用一阶剪切变形模型研究了热环境下具有温变材料属性的预应力复合材料层合板的振动行为。Fazzolari和Carrera[6]提出了分层三角里兹公式,并利用该公式研究了热环境下具有复合材料层合面板的夹层板的自由振动。他们[7]还利用该公式研究了预屈曲和后屈曲的各向异性复合材料层合板的自由振动响应。Liu和Li[8]采用一个等效非经典模型研究了受到集中简谐激励力和热载荷的由两种各向同性材料组成的矩形夹层板的振动和声学响应。Kim等[9]利用一阶剪切变形模型研究了受到电磁场和热场载荷作用的复合材料层合板的振动和稳定性问题。Li等[10]利用一阶剪切变形模型研究了热环境下非对称矩形复合材料层合板的振动和声辐射响应。Li等[11-12]利用分段剪切变形模型研究了热环境下复合材料层合板和夹层板的振动和声学响应特性。Du等[13]利用一阶剪切变形模型和von Karman非线性应变-位移关系研究了沿厚度方向具有温度梯度的复合材料层合板的振动和声学响应。
此外,还有许多学者运用数值方法研究了热环境下复合材料层合板和夹层板结构的振动问题。Oh等[14]利用分层模型建立了受到热压电载荷的压电复合材料层合板振动分析的非线性有限元方程。Makhecha等[15]以高阶zigzag模型为基础发展了一种用于热/机械载荷作用下厚复合材料层合板动力学分析的C0连续8节点四边形板单元。Ganapathi等[16]利用上述单元对热/机械载荷作用下的厚复合材料层合板和夹层板进行了非线性动力学分析。Parhi等[17]以一阶剪切变形模型为基础提出了一种用于湿热环境下多分层双曲壳动力学分析的二次等参单元。Patel等[18]以高阶zigzag模型为基础发展了一种用于湿热环境下厚复合材料层合板静力学和动力学分析的C0连续8节点四边形板单元。Tawfik等[19]利用基于von Karman非线性应变-位移关系的非线性有限元模型研究了受到气动力和热载荷的嵌入形状記忆合金的各向同性板的热屈曲和气弹行为。Hong和Jane[20]采用广义微分求积方法研究了受到正弦变化时变温度载荷的正交铺设复合材料层合板的层间应力和变形。Oh和Cho[21]以高阶zigzag模型为基础发展了一种用于更加精确预示复合材料层合板热-电-机耦合行为的3节点三角形单元,其中位移场和温度场均是由全局三次光滑场和线性zigzag场叠加而成的。Park等[22]利用一阶剪切变形模型建立了受到热载荷的嵌入形状记忆合金的复合材料层合板振动分析的非线性有限元方程,并且研究了板在预屈曲和后屈曲状态下的振动特性。Rao和Sinha[23]发展了一种用于研究湿度和温度对多向复合材料板振动响应影响的20节点六面体等参单元。Shiau和Kuo[24]发展了一种用于热屈曲夹层板自由振动分析的每个节点具有24个自由度的3节点三角形板单元。Singha等[25]采用基于一阶剪切变形模型的4节点四边形研究了热环境下复合材料斜板的小幅振动特性。Vangipuram和Ganesan[26]利用有限元方法研究了热环境下具有温变材料属性黏弹性芯层的矩形复合材料黏弹性夹层板的自由振动和阻尼特性。Pradeep和Ganesan[27]研究了多层矩形黏弹性夹层板的热屈曲和振动特性。Jeyaraj等[28-29]利用基于经典层合板模型的4节点四边形板单元研究了温度对受到简谐激励力的复合材料层合板和多层黏弹性夹层板的振动和声学响应特性的影响。Rath和Sahu[30]采用基于一阶剪切变形模型的8节点四边形等参板单元执行了湿热环境下编织纤维复合材料层合板的自由振动分析。Ibrahim等[31]利用一阶剪切变形模型和von Karman非线性应变-位移关系建立了用于受到热载荷和气动载荷的混合形状记忆合金的复合材料层合板的非线性颤振分析的非线性有限元模型。Shariyat[32]提出了一个用于受到热-机载荷的夹层板的静力学和动力学分析的全局-局部高阶剪切变形模型,并且基于该模型发展出了一个C1连续的Hermitian矩形板单元。Panda等[33]利用基于一阶剪切变形模型的8节点四边形等参板单元研究了受到温湿载荷的分层复合材料层合板的自由振动问题。Natarajan等[34]利用一阶剪切变形模型和扩展有限元方法研究了水分浓度和温度梯度对复合材料层合板自由振动和屈曲特性的影响。Zhang等[35]运用实验和数值方法研究了受到四边自由边界条件和极端热载荷的具有陶瓷泡沫芯层的纤维增强莫来石夹层板的振动特性。Katariya和Panda[36]采用基于高阶剪切变形模型的每个节点具有10个自由度的9节点等参Lagrangian单元研究了复合材料双曲壳的热屈曲和振动行为。Zhao等[37]提出了复合材料板结构分段剪切变形模型,并以该模型为基础构建了一种用于复合材料板结构热振分析的4节点四边形等参板单元。与现有的分层模型、zigzag模型和等效单层模型相比,分段剪切变形模型可以用较小的计算量获得足够精确的计算结果。
第2期赵锐,等: 时变热环境下复合材料夹层板结构动力学响应分析振 动 工 程 学 报第31卷在上述关于热环境下复合材料板结构振动分析的研究工作中,热环境均被假设为不随时间变化的恒定温度场,此时的复合材料板结构是时不变结构。然而,当高超声速飞行器在大气中高速飞行时,气动热载荷是随时间变化的,结构内的温度场也是随时间变化的,此时的复合材料板结构是时变结构。针对这种情况,本文提出了一种用于时变温度环境下复合材料夹层板结构动力学响应计算的数值仿真分析方法。首先,利用基于分段剪切变形理论的板单元建立了考虑热环境影响的复合材料夹层板结构有限元模型。然后,利用时变结构时间有限元方法计算了时变温度环境下复合材料夹层板结构的动力学响应。最后,对动态响应进行时频分析,并与由理论模态分析方法计算出的固有频率参考值进行对比,验证了本文提出的方法的有效性与精确性。
1热环境下复合材料夹层板结构有限元模型〖*2〗1.1分段剪切变形模型在分段剪切变形模型[37]中,复合材料层合板/夹层板沿着厚度方向被划分为若干段,其中每一段既可以是单层正交各向异性材料也可以是多层层合复合材料。在本研究中,复合材料夹层板结构沿厚度方向划分的段数为3段,如图1所示。
图1复合材料夹层板分段运动的一维表示
Fig.1One dimensional representation of piecewise kinematics of composite sandwich plates
在分段剪切变形模型[37]中,假设层合板内的横向位移沿着厚度方向是不变的,假设每一段的横截面在变形后依旧保持为平面,假设相邻段界面处的位移是连续的,则复合材料层合板结构第1,2,3段的位移场可以表达为:u1=u0+zbiψx2+z-zbiψx1
v1=v0+zbiψy2+z-zbiψy1
w1=w0 (1)
u2=u0+zψx2
v2=v0+zψy2
w2=w0(2)
u3=u0+ztiψx2+z-ztiψx3
v3=v0+ztiψy2+z-ztiψy3
w3=w0(3)式中u0,v0,w0分别表示位于层合板中面上的点沿着x,y,z轴方向的位移;uj,vj,wj分别表示位于层合板第j段(j=1,2,3)上的点沿着x,y,z轴方向的位移;Ψxj,Ψyj分别表示层合板第j段(j=1,2,3)横截面法线绕着y轴和x轴的转角。
1.2系统运动控制方程
利用基于分段剪切變形模型的4节点四边形层合板单元(PSDT-Quad4单元)[37]可以建立起热环境下复合材料夹层板结构的有限元模型。由该有限元模型得到的热环境下复合材料板结构运动控制方程,包括静态变形运动控制方程(即静力学方程)和相对于静平衡位置的动态变形运动控制方程(即动力学方程)[37]:K0qs=FΔT+Fs(4)
Md+Cd+K0+Kσqd=Fd(5)式中M,C,K0分别表示复合材料夹层板结构的质量、阻尼和刚度矩阵;Fs和Fd分别表示静态和动态机械外力向量;F△T表示热载荷等效节点力向量;Kσ表示由预应力引起的几何刚度矩阵;qs和qd分别表示结构的静态和动态变形。由方程(5)可以看出,由机械和热载荷引起的预应力将改变复合材料层合板结构的刚度属性,进而将影响层合板结构的固有频率、振型和其他动力学特性。
上述有限元方程不仅可以用于稳态均匀热环境下复合材料板结构的振动分析,还可以用于瞬态均匀热环境下复合材料板结构的振动分析。如果结构温度场T是随时间变化的,那么复合材料夹层板结构的几何刚度矩阵Kσ也将随着时间变化,即Kσ=Kσ(t)。此外,如果材料的弹性模量是随温度变化的,那么复合材料板结构的刚度矩阵K0也将随时间变化,即K0=K0(t)。也就是说,在瞬态热环境下,复合材料板结构运动控制方程中的刚度矩阵将变为关于时间的函数,所以瞬态热环境下的复合材料板结构属于线性时变结构。因此,瞬态热环境下复合材料板结构的振动问题属于线性时变结构动力学问题,建立的系统动力学方程是时变系统常微分方程。首先,针对不同时刻的温度载荷对静力学方程进行求解可以计算出这些时刻的静态变形,然后由这些静态变形可以进一步计算出预应力以及对应的几何刚度矩阵,最后可以利用线性时变结构动响应数值算法对动力学方程进行数值求解。
2线性时变结构时间有限元算法
线性时变结构动力学方程的一般表达式为Mtt+Ctt+Ktqt=Ft(6)在一个典型的时间单元[tk-1,tk]内,利用Galerkin方法,广义坐标q、广义速度v、广义力F、广义系统矩阵M,C,K可以分别近似为:q=ΦT×, =T×, v=ΨT×,
=T×, M=LTM×, C=LTC×,
K=LTK×, F=NT×(7)式中“×”表示复合矩阵乘法[38,40];Φ,Ψ,N,LM, LC,LK分别为用于近似变量q,v,F,M,C,K的插值基函数。
由文献[38]可知,线性时变结构不协调时间有限元算法(TFEM算法)的递推公式为D11×D12×
D21×DM22×+DC22×=
g1
g2+0
DFI(8)式中,“”表示克罗内克积,I表示单位矩阵,且有:D11=∫tktk-1ΦTLTM+ΨΦTTMdt-
ΨΦTLTMtk(9)
D12=∫tktk-1ΨΨTLTMdt(10)
D21=-∫tktk-1ΦΦTLTKdt(11)
DM22=∫tktk-1ΨTLTM+ΦΨTTMdt-
ΦΨTLTMtk(12)
DC22=-∫tktk-1ΦΨTLTCdt(13)
DF=-∫tktk-1ΦNTdt(14)3时变温度环境下复合材料夹层板结构瞬态响应分析在本节中,将联合使用分段剪切变形板单元和不协调时间有限元算法对瞬态均匀热环境下复合材料板结构的动力学问题进行数值仿真。本算例的研究对象为受到四边简支边界条件和均匀热载荷的具有正交各向异性面板和各向同性芯层的矩形夹层板。复合材料夹层板结构的几何尺寸为0.4 m×0.3 m×0.01 m,其中面板和芯层的厚度分别为0.5 mm和9 mm。面板的材料属性如下:Ef1=132 GPa, Ef2=10.3 GPa,
Gf12=Gf13=6.5 GPa, Gf23=3.91 GPa,
νf12=0.25, ρf=1570 kg/m3,
αf1=1.2×10-6/℃, αf2=2.4×10-5/℃芯层的材料属性如下:Ec=10 MPa, νc=0.3, ρc=40 kg/m3,
αc=1.8×10-7/℃參考温度为0℃。夹层板的结构阻尼系数为0.001。夹层板的铺层顺序为[0°/Core/0°]。假设材料参数是不随温度变化的。假设在夹层板结构(0.1 m,0.1 m,0.0 m)位置沿z轴方向施加一个集中随机激励力,其时域曲线和功率谱密度函数如图2所示。
图2集中激励力的时域曲线和功率谱密度函数
Fig.2Time domain curve and power spectral density function of the single exciting force图3作用在夹层板结构上的温度载荷的时域曲线
Fig.3Time domain curves of the temperature load acting on the sandwich plate structure同时,还选择该点作为响应测量点,测量方向沿z轴方向。假设作用在夹层板结构上的温度载荷曲线随时间线性增加,如图3所示。本算例的仿真总时长为5 s,选取的计算时间步长为Δt=1/3000 s。
图4瞬态热环境下复合材料夹层板结构位移响应
Fig.4Displacement responses of a composite sandwich plate in a time-varying thermal environment
图5瞬态热环境下复合材料夹层板结构速度响应
Fig.5Velocity responses of a composite sandwich plate in a time-varying thermal environment图4和5给出了利用TFEM-2242算法[38]和Newmark算法[39]计算得到的瞬态热环境下复合材料夹层板的位移和速度响应数值解。从该图中可以看出,由TFEM-2242算法和Newmark算法计算得到的振动响应的量级是基本一致的。
图6由TFEM-2242算法计算得到的夹层板结构速度响应的时频谱图(“---”表示由理论模态分析方法计算得到的固有频率参考解)
Fig.6Time-frequency spectrum of velocity response of composite sandwich plate calculated by TFEM-2242 method (“---” denotes the reference natural frequencies calculated by the theoretical modal analysis method)
图7由Newmark算法计算得到的夹层板结构速度响应的时频谱图(“---”表示由理论模态分析方法计算得到的固有频率参考解)
Fig.7Time-frequency spectrum of velocity response of composite sandwich plate calculated by Newmark method (“---” denotes the reference natural frequencies calculated by the theoretical modal analysis method)
图6和7给出了由TFEM-2242算法和Newmark算法计算得到的速度响应数值解的时频谱图,并且将由理论模态分析方法计算得到的系统各阶固有频率作为参考解。从该图中可以看出,TFEM-2242算法的数值解的频率信息与参考解吻合较好,该数值解能够准确地反映出系统固有频率随时间的变化情况,而Newmark算法的数值解的频率信息与参考解之间差异较大,这是因为Newmark算法具有显著的频散特性,进而导致了从数值解中辨识出的系统各阶固有频率明显偏小。
4结论
本文提出了一种用于时变温度环境下复合材料夹层板结构动力学响应计算的数值仿真分析方法。首先,利用基于分段剪切变形模型的板单元(PSDT-Quad4单元)建立考虑热环境影响的复合材料夹层板结构有限元模型。然后,利用线性时变结构不协调时间有限元算法(TFEM-2242算法)计算时变温度环境下复合材料夹层板结构的动力学响应。最后,对动响应进行时频分析,并与由理论模态分析方法计算得到的固有频率参考值进行对比,验证了本文提出的方法的有效性与精确性。
数值结果表明,TFEM-2242算法数值解的频率信息与参考解吻合较好,数值解能够准确地反映出系统固有频率随时间的变化情况,而Newmark算法数值解的频率信息与参考解之间差异较大。TFEM-2242算法适用于瞬态热环境下复合材料板结构的瞬态响应分析问题,并且其计算精度高于Newmark算法。
本文提出的数值仿真分析方法可以有效地预示时变热环境下复合材料夹层板结构的热振响应,为热环境下复合材料夹层板结构的设计与分析提供了理论基础。
參考文献:
[1]Huang X L, Shen H S, Zheng J J. Nonlinear vibration and dynamic response of shear deformable laminated plates in hygrothermal environments [J]. Composites Science and Technology,2004, 64(10-11):1419—1435.
[2]Girish J, Ramachandra L S. Thermal postbuckled vibrations of symmetrically laminated composite plates with initial geometric imperfections [J]. Journal of Sound and Vibration, 2005, 282(3-5):1137—1153.
[3]Matsunaga H. Free vibration and stability of angle-ply laminated composite and sandwich plates under thermal loading [J]. Composite Structures, 2007, 77(2):249—262.
[4]Li Z, Chen X, Yu H. Large-amplitude vibration analysis of shear deformable laminated composite cylindrical shells with initial imperfections in thermal environments [J]. Journal of Engineering Mechanics, 2012, 140(3):552—565.
[5]Chen C S, Chen C W, Chen W R, et al. Thermally induced vibration and stability of laminated composite plates with temperature-dependent properties [J]. Meccanica, 2013, 48(9):2311—2323.
[6]Fazzolari F A, Carrera E. Free vibration analysis of sandwich plates with anisotropic face sheets in thermal environment by using the hierarchical trigonometric Ritz formulation [J]. Composites Part B: Engineering, 2013, 50:67—81.
[7]Fazzolari F A, Carrera E. Accurate free vibration analysis of thermo-mechanically pre/post-buckled anisotropic multilayered plates based on a refined hierarchical trigonometric Ritz formulation [J]. Composite Structures, 2013, 95:381—402.
[8]Liu Y, Li Y. Vibration and acoustic response of rectangular sandwich plate under thermal environment [J]. Shock and Vibration, 2013, 20(5):1011—1030.
[9]Kim S K, Choi J, Park S, et al. Vibration and stability of laminated composite plates subjected to a combined electromagnetic and thermal field [J]. Journal of Vibration and Control, 2015, 21(12):2325—2339.
[10]Li W, Li Y. Vibration and sound radiation of an asymmetric laminated plate in thermal environments [J]. Acta Mechanica Solida Sinica, 2015, 28(1):11—22.
[11]Li X, Yu K, Han J, et al. A piecewise shear deformation theory for free vibration of composite and sandwich panels [J]. Composite Structures, 2015, 124:111—119.
[12]Li X, Yu K. Vibration and acoustic responses of composite and sandwich panels under thermal environment [J]. Composite Structures, 2015, 131:1040—1049.
[13]Du M, Geng Q, Li Y. Vibrational and acoustic responses of a laminated plate with temperature gradient along the thickness [J]. Composite Structures, 2016, 157:483—493.
[14]Oh I K, Han J H, Lee I. Postbuckling and vibration characteristics of piezolaminated composite plate subject to thermo-piezoelectric loads [J]. Journal of Sound and Vibration, 2000, 233(1):19—40.
[15]Makhecha D P, Ganapathi M, Patel B P. Dynamic analysis of laminated composite plates subjected to thermal/mechanical loads using an accurate theory [J]. Composite Structures, 2001, 51(3):221—236.
[16]Ganapathi M, Patel B P, Makhecha D P. Nonlinear dynamic analysis of thick composite/sandwich laminates using an accurate higher-order theory [J]. Composites Part B: Engineering, 2004, 35(4):345—355.
[17]Parhi P K, Bhattacharyya S K, Sinha P K. Hygrothermal effects on the dynamic behavior of multiple delaminated composite plates and shells [J]. Journal of Sound and Vibration, 2001, 248(2):195—214.
[18]Patel B P, Ganapathi M, Makhecha D P. Hygrothermal effects on the structural behaviour of thick composite laminates using higher-order theory [J]. Composite Structures, 2002, 56(1):25—34.
[19]Tawfik M, Ro J J, Mei C. Thermal post-buckling and aeroelastic behaviour of shape memory alloy reinforced plates [J]. Smart Materials and Structures, 2002, 11(2):297—307.
[20]Hong C C, Jane K C. Shear deformation in thermal vibration analysis of laminated plates by the GDQ method [J]. International Journal of Mechanical Sciences, 2003, 45(1):21—36.
[21]Oh J, Cho M. A finite element based on cubic zig-zag plate theory for the prediction of thermo-electric-mechanical behaviors [J]. International Journal of Solids and Structures, 2004, 41(5):1357—1375.
[22]Park J S, Kim J H, Moon S H. Vibration of thermally post-buckled composite plates embedded with shape memory alloy fibers [J]. Composite Structures, 2004, 63(2):179—188.
[23]Rao V V S, Sinha P K. Dynamic response of multidirectional composites in hygrothermal environments [J]. Composite Structures, 2004, 64(3):329—338.
[24]Shiau L C, Kuo S Y. Free vibration of thermally buckled composite sandwich plates [J]. Journal of Vibration and Acoustics, 2006, 128(1):1—7.
[25]Singha M K, Ramachandra L S, Bandyopadhyay J N. Vibration behavior of thermally stressed composite skew plate [J]. Journal of Sound and Vibration, 2006, 296(4-5):1093—1102.
[26]Vangipuram P, Ganesan N. Buckling and vibration of rectangular composite viscoelastic sandwich plates under thermal loads [J]. Composite Structures, 2007, 77(4):419—429.
[27]Pradeep V, Ganesan N. Thermal buckling and vibration behavior of multi-layer rectangular viscoelastic sandwich plates [J]. Journal of Sound and Vibration, 2008, 310(1-2):169—183.
[28]Jeyaraj P, Ganesan N, Padmanabhan C. Vibration and acoustic response of a composite plate with inherent material damping in a thermal environment [J]. Journal of Sound and Vibration, 2009, 320(1-2):322—338.
[29]Jeyaraj P, Padmanabhan C, Ganesan N. Vibro-acoustic behavior of a multilayered viscoelastic sandwich plate under a thermal environment [J]. Journal of Sandwich Structures and Materials, 2011, 13(5):509—537.
[30]Rath M, Sahu S. Vibration of woven fiber laminated composite plates in hygrothermal environment [J]. Journal of Vibration and Control, 2012, 18(13):1957—1970.
[31]Ibrahim H H, Tawfik M, Negm H M. Thermal buckling and nonlinear flutter behavior of shape memory alloy hybrid composite plates [J]. Journal of Vibration and Control, 2011, 17(3):321—333.
[32]Shariyat M. A generalized global-local high-order theory for bending and vibration analyses of sandwich plates subjected to thermo-mechanical loads [J]. International Journal of Mechanical Sciences, 2010, 52(3):495—514.
[33]Panda H S, Sahu S K, Parhi P K. Hygrothermal effects on free vibration of delaminated woven fiber composite plates - Numerical and experimental results [J]. Composite Structures, 2013, 96:502—513.
[34]Natarajan S, Deogekar P S, Manickam G, et al. Hygrothermal effects on the free vibration and buckling of laminated composites with cutouts [J]. Composite Structures, 2014, 108:848—855.
[35]Zhang X, Yu K, Bai Y, et al. Thermal vibration characteristics of fiber-reinforced mullite sandwich structure with ceramic foams core [J]. Composite Structures, 2015, 131:99—106.
[36]Katariya P V, Panda S K. Thermal buckling and vibration analysis of laminated composite curved shell panel [J]. Aircraft Engineering and Aerospace Technology, 2016, 88(1):97—107.
[37]Zhao R, Yu K, Hulbert G M, et al. Piecewise shear deformation theory and finite element formulation for vibration analysis of laminated composite and sandwich plates in thermal environments [J]. Composite Structures, 2017, 160:1060—1083.
[38]Zhao R, Yu K, Hulbert G M. Time discontinuous finite element method for transient response analysis of linear time-varying structures [J]. Meccanica, 2018,53(4-5):703—726.
[39]Zhao R, Yu K. An efficient transient analysis method for linear time-varying structures based on multi-level substructuring method [J]. Computers & Structures, 2015, 146:76—90.
[40]Zhao R, Yu K. Hamilton′s law of variable mass system and time finite element formulations for time-varying structures based on the law [J]. International Journal for Numerical Methods in Engineering, 2014, 99(10):711—736.
Vibration response analysis of a composite sandwich plate under a
time-varying thermal environmentZHAO Rui1 , YU Kai-ping1 , CUI Nai-gang2 (1. Department of Astronautic Science and Mechanics, Harbin Institute of Technology, Harbin 150001, China;
2. Department of Astronautic Engineering, Harbin Institute of Technology, Harbin 150001, China)
Abstract: The composite structure has been widely used in the aerospace engineering. When the aircraft is flying at high speed in the atmosphere, the aerodynamic heat load will change the dynamic characteristic and dynamic response of the composite structure. At present, the numerical simulation of the dynamic response of composite structures in constant temperature environment has been studied by scholars, while the numerical simulation in the time-varying temperature environment has not been studied yet. In this paper, a numerical simulation analysis method for the dynamic response analysis of composite sandwich plates in time-varying temperature environments is proposed. Firstly, the finite element model of composite sandwich plates is established utilizing the plate element based on the piecewise shear deformation theory. And then the dynamic response of composite sandwich plates under the time-varying temperature environment is calculated by using the time finite element method for time-varying structures. Finally, the time-frequency analysis of the dynamic response is performed and the results are compared with the reference natural frequencies obtained using the theoretical modal analysis, by which the validity and accuracy of the proposed method are verified. The numerical simulation analysis method proposed in this paper can effectively predict the thermal vibration response of composite sandwich plates in time-varying temperature environments, and provides a theoretical basis for the design and analysis of composite structures in thermal environment.
Key words: structural vibration; composite structure; thermal vibration analysis; time-varying structure; time integration algorithm

