基于逻辑回归算法的乳腺癌诊断数据分类研究
刘蕾
摘 要:乳腺癌是世界范圍内妇女死亡的主要原因之一,准确的诊断是乳腺癌治疗中最重要的步骤之一。本文详细讲解了逻辑回归模型的原理知识,结合Sklearn机器学习库的LogisticRegression算法对乳腺癌威斯康辛(诊断)数据集进行了数据分类。由于该数据集分类标签划分为两类(恶性、良性),能够很好地适用于逻辑回归模型。用基于两个特征的逻辑回归模型得到的分类结果表明,当选取平均半径和最大周长两个特征时,分类精度最高(95.72%)。与以往的方法相比,该方法在性能上有所提高。
关键词:乳腺癌数据集;逻辑回归分类算法;预测
中图分类号:TP393 文献标识码:A
Abstract:Breast cancer is one of the major causes of death for women worldwide,and accurate diagnosis is one of the most important steps in the treatment of breast cancer.This paper explains the knowledge of the logistic regression model in detail,and classifies the data set of breast cancer by using the Logistic Regression algorithm of Sklearn machine learning library.The classification label of the data set is divided into 2 classes (malignant and benign),which is appropriate for the logistic regression model.The classification results based on the logistic regression model with two features show that the classification accuracy is the highest (95.72%) when the two characteristics of the mean radius and the largest perimeter are selected.In comparison to previous methods,the performance has been improved to some extent.
Keywords:breast cancer data set;logistic regression classification algorithm;prediction
1 引言(Introduction)
乳腺癌的早期诊断与治疗有着重要的作用,已有多种分类方法应用于此种诊断,如C4.5决策树算法、朴素贝叶斯算法、支持向量机、KNN等。基于乳腺癌数据,运用上述分类方法进行模型构建,分析比较各模型性能,其中支持向量机性能较优。支持向量机可有效调节算法复杂度与泛化能力之间的矛盾,其在小样本学习领域中有着优于传统模式识别方法的推广能力。然而在处理较大规模数据集时,往往需要较长的训练时间。KNN方法是一种基于实例的学习,可生成任意形状的决策边界,无需建立模型,但其分类中开销很大,需逐个计算相似度,此外,当k取值较小时,对噪声也很敏感[1]。针对上述不足,国内外研究者们也已做出相应的改进,但尚未有一个能同时实现训练时间短、预测能力强、规则提取简易且适应性强的分类方法[2]。本文采用的逻辑回归分类方法是一种logistic方程归一化后的线性回归。这种归一化的方法往往比较合理,能够打压过大和过小的结果(往往是噪音),以保证主流的结果不至于被忽视。同时模型易于解释,便于提取规则,对噪声干扰及冗余属性也有着相当好的鲁棒性[3]。
2 乳腺癌威斯康辛数据集(Wisconsin breast cancer data set)
本文所用的癌症数据来自加州大学欧文分校机器学习数据集仓库中的威斯康辛州乳腺癌数据集。该数据集共有569个数据点,每个数据点有30个属性。属性来源于乳房硬块的细针穿刺(FNA)数字影像,分别是影像中细胞核的10种特征的最大值、平均值、方差。这10种特征包括半径、周长、面积、质地、致密性、平滑度、凹度、凹点数、对称性、分形维度等。具体属性说明如表1所示。
breast_cancer里有两个属性data、target。data是一个矩阵。每一列代表30个属性中的一个,一共30列;每一行代表某个被测量的乳房硬块数字影像。一共采样了569条记录。
输出如下所示:
[[ 1.79900000e+01 1.03800000e+01 1.22800000e+02 ..., 2.65400000e-01
4.60100000e-01 1.18900000e-01]
[ 2.05700000e+01 1.77700000e+01 1.32900000e+02 ..., 1.86000000e-01
2.75000000e-01 8.90200000e-02]
[ 1.96900000e+01 2.12500000e+01 1.30000000e+02 ..., 2.43000000e-01
3.61300000e-01 8.75800000e-02]
...,
[ 1.66000000e+01 2.80800000e+01 1.08300000e+02 ..., 1.41800000e-01
2.21800000e-01 7.82000000e-02]
[ 2.06000000e+01 2.93300000e+01 1.40100000e+02 ..., 2.65000000e-01
4.08700000e-01 1.24000000e-01]
[ 7.76000000e+00 2.45400000e+01 4.79200000e+01 ..., 0.00000000e+00
2.87100000e-01 7.03900000e-02]]
target是一个数组,存储了data中每条记录属于哪一类肿瘤,所以数组的长度是569。因为数组元素的值共有2类,所以不同值只有2个,0代表恶性,1代表良性。
输出分类标签的结果如下:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 1 0 1 1 1 1 1 0 0 1 0 0 1 1 1 1 0 1 0 0 1 1 1 1 0 1 0 0
……
1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0 0 0 0 0 0 1]
3 散点图绘制(Drawing scatter plot)
散点图是数据点在直角坐标系平面上的分布图,适用于表示因变量随自变量而变化的大致趋势,据此可以选择合适的函数对数据点进行拟合。
载入乳腺癌数据集,然后区分其中的恶性样本数据和良性样本数据,分别存入数据集Benign和Malignent,获得良性样本357个,恶性样本212个。
从良性样本和恶性样本中分别提取出两列数据,即平均半径和平均纹理,获取的值赋值给XB、YB、XM、YM变量。最后调用scatter()函数绘制散点图。关键代码如下:
plt.scatter(XM[:50], YM[:50], color='red', marker='o', label='malignent')绘制前50个恶性样本,以红色圆点标记。
plt.scatter(XB[:50], YB[:50], color='blue', marker='x', label='benign')绘制前50个良性样本,以蓝色叉号标记。
绘制的散点图如图1所示。
由该散点图可以得出结论:恶性肿瘤的判别与肿瘤的半径大小及纹理程度都有直接关联。该图为此论断提供了可靠的数据依据。
4 逻辑回归分析(Logistic regression analysis)
下面采用逻辑回归对其进行分类预测。
获取样本的两列数据,对应为平均半径和平均纹理,每个点的坐标就是(x,y)。先取二维数组的第一列(平均半径)的最小值、最大值和步长(设置为0.02)生成数组,再取二维数组的第二列(平均纹理)的最小值、最大值和步长生成数组,最后生成两个网格矩阵xx和yy,如下所示。
[[ 6.481 6.501 6.521 ..., 28.561 28.581 28.601]
[ 6.481 6.501 6.521 ..., 28.561 28.581 28.601]
[ 6.481 6.501 6.521 ..., 28.561 28.581 28.601]
...,
[ 6.481 6.501 6.521 ..., 28.561 28.581 28.601]
[ 6.481 6.501 6.521 ..., 28.561 28.581 28.601]
[ 6.481 6.501 6.521 ..., 28.561 28.581 28.601]]
[[ 9.21 9.21 9.21 ..., 9.21 9.21 9.21]
[ 9.23 9.23 9.23 ..., 9.23 9.23 9.23]
[ 9.25 9.25 9.25 ..., 9.25 9.25 9.25]
...,
[ 39.73 39.73 39.73 ..., 39.73 39.73 39.73]
[ 39.75 39.75 39.75 ..., 39.75 39.75 39.75]
[ 39.77 39.77 39.77 ..., 39.77 39.77 39.77]]
将xx和yy的两个矩阵降维成一维数组。由于两个矩阵大小相等,因此两个一维数组大小也相等。把第一列(平均半径)数据按步长取等分,作为行,并复制多行得到xx網格矩阵;再把第二列(平均纹理)数据按步长取等分,作为列,并复制多列得到yy网格矩阵;最后将xx和yy矩阵都变成两个一维数组,再组合成一个二维数组进行预测。
对于病人的特征,使用如下公式计算得到危险分数[4]。
计算得到的分数越高,风险越大;分数越低,风险越小。s的取值范围是(-∞,+∞),但是我们想要的是一个[0,1]之间的值。因此需要一个转换函数来把这个分数转换成[0,1]之间的值。这个函数称为Logistic函数,Logistic函数是一个S形的函数,形状如图2所示。
这个函数也称为sigmoid函数。这个函数能够把s映射到[0,1]之间,我们把这个函数称为θ(s)。Logistic函数的形式为[5]:
使用Python语言机器学习库SKLearn提供的函数LogisticRegression进行运算,获得的预测结果如下。
[1 1 1 ..., 0 0 0]
Size:1692603
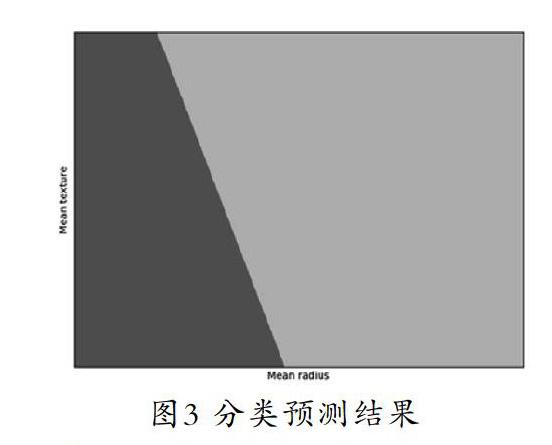
将xx、yy两个网格矩阵和对应的预测结果绘制在图上,可以发现输出为两个颜色区块,分别表示分类的两类区域。输出的区域如图3所示。
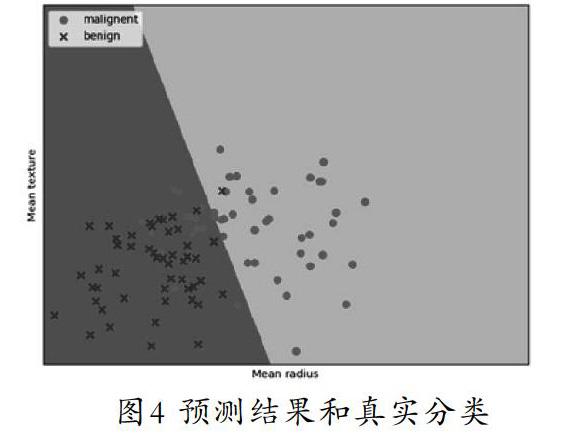
从恶性样本、良性样本分别获取前50个样本数据,调用scatter()绘制散点图。第一个参数为第一列数据(平均半径),第二个参数为第二列数据(平均纹理),最后标记为malignent或benign。输出的区域如图4所示。
图4经过逻辑回归后划分为两个区域。右侧浅蓝色部分,对应Malignent恶性;左侧棕红色部分,对应Benign良性。散点图为各数据点真实的分类,红色的圆点对应Malignent恶性,蓝色星形对应Benign良性。划分的两个区域为数据点预测的类型,预测的分类结果与训练数据的真实结果基本一致,可见模型能够很好地拟合决策面。
5 结论(Conclusion)
实验中,当选择平均半径和平均纹理两个特性进行分类,使用全部训练样本后,分类精度最高可达到90.48%;而选择平均半径和最大周长两个特性时,分类精度达到95.72%,因此,选择更优的特征组合将提高分类精度。实验结果表明,逻辑回归分类模型实现了快速、简便、高效的乳腺癌诊断,可以帮助诊断乳腺癌。本实验采用的威斯康星乳腺癌诊断测试(WDBC)数据集来自于加利福尼亚大学Irvine机器学习库。训练阶段从32个原始特征中提取肿瘤特征。结果不仅说明了该方法对乳腺癌诊断的能力,而且显示了在训练阶段的时间节省。通过更好地提取不同类型肿瘤的特征屬性,能够有效提高该方法的分类准确率,医生也可以从抽象的肿瘤特征中获益。
参考文献(References)
[1] L Miclet,S Bayoudh,A Delhay.Analogical Dissimilarity:Definition,Algorithms and Two Experiments in Machine Learning[J].Journal of Artificial Intelligence Research,2014,32(3):793-824.
[2] CW Han.Breast Cancer Diagnosis using Logic-based Fuzzy Neural Networks[J].Digital Contents & Applications,2016:69-72.
[3] Emina , Abdulhamit Subasi.Breast Cancer Diagnosis using GA Feature Selection and Rotation Forest[J].Neural Computing & Applications,2017,28(4):753-763.
[4] 毛林,陆全华,程涛.基于高维数据的集成逻辑回归分类算法的研究与应用[J].科技通报,2013(12):64-66.
[5] 谢忠红,张颖,张琳.基于逻辑回归算法的微博水军识别[J].微型机与应用,2017(16):67-69.
作者简介:
刘 蕾(1978-),女,硕士,副教授.研究领域:数据挖掘,大数据.



摘 要:乳腺癌是世界范圍内妇女死亡的主要原因之一,准确的诊断是乳腺癌治疗中最重要的步骤之一。本文详细讲解了逻辑回归模型的原理知识,结合Sklearn机器学习库的LogisticRegression算法对乳腺癌威斯康辛(诊断)数据集进行了数据分类。由于该数据集分类标签划分为两类(恶性、良性),能够很好地适用于逻辑回归模型。用基于两个特征的逻辑回归模型得到的分类结果表明,当选取平均半径和最大周长两个特征时,分类精度最高(95.72%)。与以往的方法相比,该方法在性能上有所提高。
关键词:乳腺癌数据集;逻辑回归分类算法;预测
中图分类号:TP393 文献标识码:A
Abstract:Breast cancer is one of the major causes of death for women worldwide,and accurate diagnosis is one of the most important steps in the treatment of breast cancer.This paper explains the knowledge of the logistic regression model in detail,and classifies the data set of breast cancer by using the Logistic Regression algorithm of Sklearn machine learning library.The classification label of the data set is divided into 2 classes (malignant and benign),which is appropriate for the logistic regression model.The classification results based on the logistic regression model with two features show that the classification accuracy is the highest (95.72%) when the two characteristics of the mean radius and the largest perimeter are selected.In comparison to previous methods,the performance has been improved to some extent.
Keywords:breast cancer data set;logistic regression classification algorithm;prediction
1 引言(Introduction)
乳腺癌的早期诊断与治疗有着重要的作用,已有多种分类方法应用于此种诊断,如C4.5决策树算法、朴素贝叶斯算法、支持向量机、KNN等。基于乳腺癌数据,运用上述分类方法进行模型构建,分析比较各模型性能,其中支持向量机性能较优。支持向量机可有效调节算法复杂度与泛化能力之间的矛盾,其在小样本学习领域中有着优于传统模式识别方法的推广能力。然而在处理较大规模数据集时,往往需要较长的训练时间。KNN方法是一种基于实例的学习,可生成任意形状的决策边界,无需建立模型,但其分类中开销很大,需逐个计算相似度,此外,当k取值较小时,对噪声也很敏感[1]。针对上述不足,国内外研究者们也已做出相应的改进,但尚未有一个能同时实现训练时间短、预测能力强、规则提取简易且适应性强的分类方法[2]。本文采用的逻辑回归分类方法是一种logistic方程归一化后的线性回归。这种归一化的方法往往比较合理,能够打压过大和过小的结果(往往是噪音),以保证主流的结果不至于被忽视。同时模型易于解释,便于提取规则,对噪声干扰及冗余属性也有着相当好的鲁棒性[3]。
2 乳腺癌威斯康辛数据集(Wisconsin breast cancer data set)
本文所用的癌症数据来自加州大学欧文分校机器学习数据集仓库中的威斯康辛州乳腺癌数据集。该数据集共有569个数据点,每个数据点有30个属性。属性来源于乳房硬块的细针穿刺(FNA)数字影像,分别是影像中细胞核的10种特征的最大值、平均值、方差。这10种特征包括半径、周长、面积、质地、致密性、平滑度、凹度、凹点数、对称性、分形维度等。具体属性说明如表1所示。
breast_cancer里有两个属性data、target。data是一个矩阵。每一列代表30个属性中的一个,一共30列;每一行代表某个被测量的乳房硬块数字影像。一共采样了569条记录。
输出如下所示:
[[ 1.79900000e+01 1.03800000e+01 1.22800000e+02 ..., 2.65400000e-01
4.60100000e-01 1.18900000e-01]
[ 2.05700000e+01 1.77700000e+01 1.32900000e+02 ..., 1.86000000e-01
2.75000000e-01 8.90200000e-02]
[ 1.96900000e+01 2.12500000e+01 1.30000000e+02 ..., 2.43000000e-01
3.61300000e-01 8.75800000e-02]
...,
[ 1.66000000e+01 2.80800000e+01 1.08300000e+02 ..., 1.41800000e-01
2.21800000e-01 7.82000000e-02]
[ 2.06000000e+01 2.93300000e+01 1.40100000e+02 ..., 2.65000000e-01
4.08700000e-01 1.24000000e-01]
[ 7.76000000e+00 2.45400000e+01 4.79200000e+01 ..., 0.00000000e+00
2.87100000e-01 7.03900000e-02]]
target是一个数组,存储了data中每条记录属于哪一类肿瘤,所以数组的长度是569。因为数组元素的值共有2类,所以不同值只有2个,0代表恶性,1代表良性。
输出分类标签的结果如下:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 1 0 1 1 1 1 1 0 0 1 0 0 1 1 1 1 0 1 0 0 1 1 1 1 0 1 0 0
……
1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0 0 0 0 0 0 1]
3 散点图绘制(Drawing scatter plot)
散点图是数据点在直角坐标系平面上的分布图,适用于表示因变量随自变量而变化的大致趋势,据此可以选择合适的函数对数据点进行拟合。
载入乳腺癌数据集,然后区分其中的恶性样本数据和良性样本数据,分别存入数据集Benign和Malignent,获得良性样本357个,恶性样本212个。
从良性样本和恶性样本中分别提取出两列数据,即平均半径和平均纹理,获取的值赋值给XB、YB、XM、YM变量。最后调用scatter()函数绘制散点图。关键代码如下:
plt.scatter(XM[:50], YM[:50], color='red', marker='o', label='malignent')绘制前50个恶性样本,以红色圆点标记。
plt.scatter(XB[:50], YB[:50], color='blue', marker='x', label='benign')绘制前50个良性样本,以蓝色叉号标记。
绘制的散点图如图1所示。
由该散点图可以得出结论:恶性肿瘤的判别与肿瘤的半径大小及纹理程度都有直接关联。该图为此论断提供了可靠的数据依据。
4 逻辑回归分析(Logistic regression analysis)
下面采用逻辑回归对其进行分类预测。
获取样本的两列数据,对应为平均半径和平均纹理,每个点的坐标就是(x,y)。先取二维数组的第一列(平均半径)的最小值、最大值和步长(设置为0.02)生成数组,再取二维数组的第二列(平均纹理)的最小值、最大值和步长生成数组,最后生成两个网格矩阵xx和yy,如下所示。
[[ 6.481 6.501 6.521 ..., 28.561 28.581 28.601]
[ 6.481 6.501 6.521 ..., 28.561 28.581 28.601]
[ 6.481 6.501 6.521 ..., 28.561 28.581 28.601]
...,
[ 6.481 6.501 6.521 ..., 28.561 28.581 28.601]
[ 6.481 6.501 6.521 ..., 28.561 28.581 28.601]
[ 6.481 6.501 6.521 ..., 28.561 28.581 28.601]]
[[ 9.21 9.21 9.21 ..., 9.21 9.21 9.21]
[ 9.23 9.23 9.23 ..., 9.23 9.23 9.23]
[ 9.25 9.25 9.25 ..., 9.25 9.25 9.25]
...,
[ 39.73 39.73 39.73 ..., 39.73 39.73 39.73]
[ 39.75 39.75 39.75 ..., 39.75 39.75 39.75]
[ 39.77 39.77 39.77 ..., 39.77 39.77 39.77]]
将xx和yy的两个矩阵降维成一维数组。由于两个矩阵大小相等,因此两个一维数组大小也相等。把第一列(平均半径)数据按步长取等分,作为行,并复制多行得到xx網格矩阵;再把第二列(平均纹理)数据按步长取等分,作为列,并复制多列得到yy网格矩阵;最后将xx和yy矩阵都变成两个一维数组,再组合成一个二维数组进行预测。
对于病人的特征,使用如下公式计算得到危险分数[4]。
计算得到的分数越高,风险越大;分数越低,风险越小。s的取值范围是(-∞,+∞),但是我们想要的是一个[0,1]之间的值。因此需要一个转换函数来把这个分数转换成[0,1]之间的值。这个函数称为Logistic函数,Logistic函数是一个S形的函数,形状如图2所示。
这个函数也称为sigmoid函数。这个函数能够把s映射到[0,1]之间,我们把这个函数称为θ(s)。Logistic函数的形式为[5]:
使用Python语言机器学习库SKLearn提供的函数LogisticRegression进行运算,获得的预测结果如下。
[1 1 1 ..., 0 0 0]
Size:1692603
将xx、yy两个网格矩阵和对应的预测结果绘制在图上,可以发现输出为两个颜色区块,分别表示分类的两类区域。输出的区域如图3所示。
从恶性样本、良性样本分别获取前50个样本数据,调用scatter()绘制散点图。第一个参数为第一列数据(平均半径),第二个参数为第二列数据(平均纹理),最后标记为malignent或benign。输出的区域如图4所示。
图4经过逻辑回归后划分为两个区域。右侧浅蓝色部分,对应Malignent恶性;左侧棕红色部分,对应Benign良性。散点图为各数据点真实的分类,红色的圆点对应Malignent恶性,蓝色星形对应Benign良性。划分的两个区域为数据点预测的类型,预测的分类结果与训练数据的真实结果基本一致,可见模型能够很好地拟合决策面。
5 结论(Conclusion)
实验中,当选择平均半径和平均纹理两个特性进行分类,使用全部训练样本后,分类精度最高可达到90.48%;而选择平均半径和最大周长两个特性时,分类精度达到95.72%,因此,选择更优的特征组合将提高分类精度。实验结果表明,逻辑回归分类模型实现了快速、简便、高效的乳腺癌诊断,可以帮助诊断乳腺癌。本实验采用的威斯康星乳腺癌诊断测试(WDBC)数据集来自于加利福尼亚大学Irvine机器学习库。训练阶段从32个原始特征中提取肿瘤特征。结果不仅说明了该方法对乳腺癌诊断的能力,而且显示了在训练阶段的时间节省。通过更好地提取不同类型肿瘤的特征屬性,能够有效提高该方法的分类准确率,医生也可以从抽象的肿瘤特征中获益。
参考文献(References)
[1] L Miclet,S Bayoudh,A Delhay.Analogical Dissimilarity:Definition,Algorithms and Two Experiments in Machine Learning[J].Journal of Artificial Intelligence Research,2014,32(3):793-824.
[2] CW Han.Breast Cancer Diagnosis using Logic-based Fuzzy Neural Networks[J].Digital Contents & Applications,2016:69-72.
[3] Emina , Abdulhamit Subasi.Breast Cancer Diagnosis using GA Feature Selection and Rotation Forest[J].Neural Computing & Applications,2017,28(4):753-763.
[4] 毛林,陆全华,程涛.基于高维数据的集成逻辑回归分类算法的研究与应用[J].科技通报,2013(12):64-66.
[5] 谢忠红,张颖,张琳.基于逻辑回归算法的微博水军识别[J].微型机与应用,2017(16):67-69.
作者简介:
刘 蕾(1978-),女,硕士,副教授.研究领域:数据挖掘,大数据.

